0391-完美矩形

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 15:32:50 2023-09-13 15:32:50 Updated    

给你一个数组 rectangles ，其中 rectangles[i] = [xi, yi, ai, bi]
表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (xi, yi) ，右上顶点是 (ai, bi) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

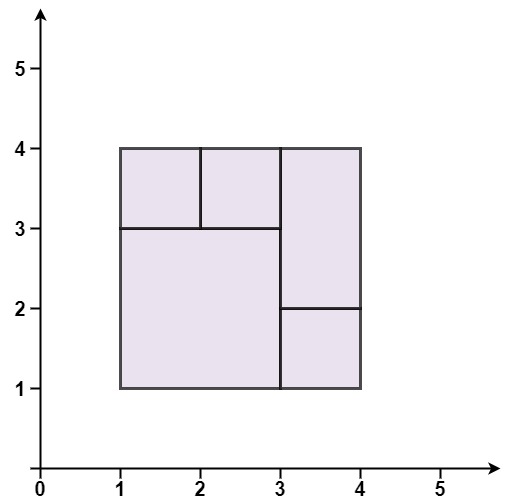
示例 1：

**输入：** rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
**输出：** true
**解释：** 5 个矩形一起可以精确地覆盖一个矩形区域。

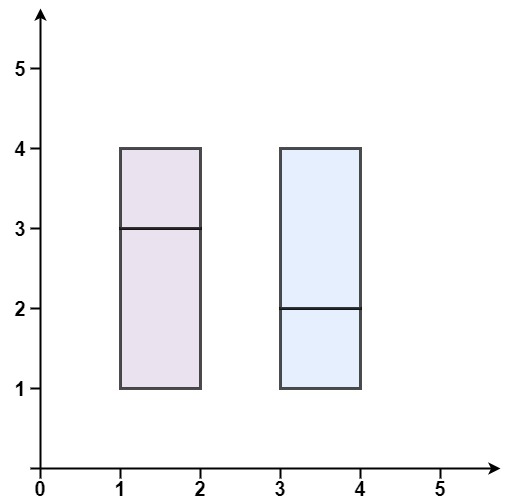
示例 2：

**输入：** rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
**输出：** false
**解释：** 两个矩形之间有间隔，无法覆盖成一个矩形。

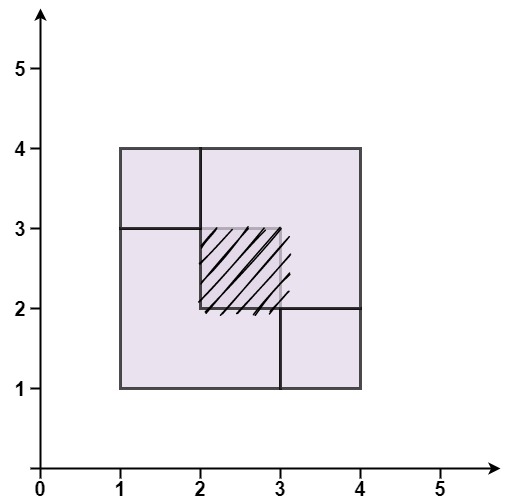
示例 3：

**输入：** rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
**输出：** false
**解释：** 因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

提示：

  • 1 <= rectangles.length <= 2 * 104
  • rectangles[i].length == 4
  • -105 <= xi, yi, ai, bi <= 105

方法一：哈希表

精确覆盖意味着：

  • 矩形区域中不能有空缺，即矩形区域的面积等于所有矩形的面积之和；
  • 矩形区域中不能有相交区域。

我们需要一个统计量来判定是否存在相交区域。由于精确覆盖意味着矩形的边和顶点会重合在一起，我们不妨统计每个矩形顶点的出现次数。同一个位置至多只能存在四个顶点，在满足该条件的前提下，如果矩形区域中有相交区域，这要么导致矩形区域四角的顶点出现不止一次，要么导致非四角的顶点存在出现一次或三次的顶点；

因此要满足精确覆盖，除了要满足矩形区域的面积等于所有矩形的面积之和，还要满足矩形区域四角的顶点只能出现一次，且其余顶点的出现次数只能是两次或四次。

在代码实现时，我们可以遍历矩形数组，计算矩形区域四个顶点的位置，以及矩形面积之和，并用哈希表统计每个矩形的顶点的出现次数。遍历完成后，检查矩形区域的面积是否等于所有矩形的面积之和，以及每个顶点的出现次数是否满足上述要求。

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution:
    def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
        area, minX, minY, maxX, maxY = 0, rectangles[0][0], rectangles[0][1], rectangles[0][2], rectangles[0][3]
        cnt = defaultdict(int)
        for rect in rectangles:
            x, y, a, b = rect[0], rect[1], rect[2], rect[3]
            area += (a - x) * (b - y)

            minX = min(minX, x)
            minY = min(minY, y)
            maxX = max(maxX, a)
            maxY = max(maxY, b)

            cnt[(x, y)] += 1
            cnt[(x, b)] += 1
            cnt[(a, y)] += 1
            cnt[(a, b)] += 1

        if area != (maxX - minX) * (maxY - minY) or cnt[(minX, minY)] != 1 or cnt[(minX, maxY)] != 1 or cnt[(maxX, minY)] != 1 or cnt[(maxX, maxY)] != 1:
            return False

        del cnt[(minX, minY)], cnt[(minX, maxY)], cnt[(maxX, minY)], cnt[(maxX, maxY)]

        return all(c == 2 or c == 4 for c in cnt.values())
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        long area = 0;
        int minX = rectangles[0][0], minY = rectangles[0][1], maxX = rectangles[0][2], maxY = rectangles[0][3];
        Map<Point, Integer> cnt = new HashMap<Point, Integer>();
        for (int[] rect : rectangles) {
            int x = rect[0], y = rect[1], a = rect[2], b = rect[3];
            area += (long) (a - x) * (b - y);

            minX = Math.min(minX, x);
            minY = Math.min(minY, y);
            maxX = Math.max(maxX, a);
            maxY = Math.max(maxY, b);

            Point point1 = new Point(x, y);
            Point point2 = new Point(x, b);
            Point point3 = new Point(a, y);
            Point point4 = new Point(a, b);

            cnt.put(point1, cnt.getOrDefault(point1, 0) + 1);
            cnt.put(point2, cnt.getOrDefault(point2, 0) + 1);
            cnt.put(point3, cnt.getOrDefault(point3, 0) + 1);
            cnt.put(point4, cnt.getOrDefault(point4, 0) + 1);
        }

        Point pointMinMin = new Point(minX, minY);
        Point pointMinMax = new Point(minX, maxY);
        Point pointMaxMin = new Point(maxX, minY);
        Point pointMaxMax = new Point(maxX, maxY);
        if (area != (long) (maxX - minX) * (maxY - minY) || cnt.getOrDefault(pointMinMin, 0) != 1 || cnt.getOrDefault(pointMinMax, 0) != 1 || cnt.getOrDefault(pointMaxMin, 0) != 1 || cnt.getOrDefault(pointMaxMax, 0) != 1) {
            return false;
        }

        cnt.remove(pointMinMin);
        cnt.remove(pointMinMax);
        cnt.remove(pointMaxMin);
        cnt.remove(pointMaxMax);

        for (Map.Entry<Point, Integer> entry : cnt.entrySet()) {
            int value = entry.getValue();
            if (value != 2 && value != 4) {
                return false;
            }
        }
        return true;
    }
}

class Point {
    int x;
    int y;

    public Point(int x, int y) {
        this.x = x;
        this.y = y;
    }

    @Override
    public int hashCode() {
        return x + y;
    }

    @Override
    public boolean equals(Object obj) {
        if (obj instanceof Point) {
            Point point2 = (Point) obj;
            return this.x == point2.x && this.y == point2.y;
        }
        return false;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
public class Solution {
    public bool IsRectangleCover(int[][] rectangles) {
        long area = 0;
        int minX = rectangles[0][0], minY = rectangles[0][1], maxX = rectangles[0][2], maxY = rectangles[0][3];
        Dictionary<Point, int> cnt = new Dictionary<Point, int>();
        foreach (int[] rect in rectangles) {
            int x = rect[0], y = rect[1], a = rect[2], b = rect[3];
            area += (long) (a - x) * (b - y);

            minX = Math.Min(minX, x);
            minY = Math.Min(minY, y);
            maxX = Math.Max(maxX, a);
            maxY = Math.Max(maxY, b);

            Point point1 = new Point(x, y);
            Point point2 = new Point(x, b);
            Point point3 = new Point(a, y);
            Point point4 = new Point(a, b);

            if (!cnt.ContainsKey(point1)) {
                cnt.Add(point1, 0);
            }
            cnt[point1]++;
            if (!cnt.ContainsKey(point2)) {
                cnt.Add(point2, 0);
            }
            cnt[point2]++;
            if (!cnt.ContainsKey(point3)) {
                cnt.Add(point3, 0);
            }
            cnt[point3]++;
            if (!cnt.ContainsKey(point4)) {
                cnt.Add(point4, 0);
            }
            cnt[point4]++;
        }

        Point pointMinMin = new Point(minX, minY);
        Point pointMinMax = new Point(minX, maxY);
        Point pointMaxMin = new Point(maxX, minY);
        Point pointMaxMax = new Point(maxX, maxY);
        if (area != (long) (maxX - minX) * (maxY - minY) || !cnt.ContainsKey(pointMinMin) || cnt[pointMinMin] != 1 || !cnt.ContainsKey(pointMinMax) || cnt[pointMinMax] != 1 || !cnt.ContainsKey(pointMaxMin) || cnt[pointMaxMin] != 1 || !cnt.ContainsKey(pointMaxMax) || cnt[pointMaxMax] != 1) {
            return false;
        }

        cnt.Remove(pointMinMin);
        cnt.Remove(pointMinMax);
        cnt.Remove(pointMaxMin);
        cnt.Remove(pointMaxMax);

        foreach (KeyValuePair<Point, int> entry in cnt) {
            int value = entry.Value;
            if (value != 2 && value != 4) {
                return false;
            }
        }
        return true;
    }
}

class Point {
    int x;
    int y;

    public Point(int x, int y) {
        this.x = x;
        this.y = y;
    }

    public override int GetHashCode() {
        return x + y;
    }

    public override bool Equals(Object obj) {
        if (obj is Point) {
            Point point2 = (Point) obj;
            return this.x == point2.x && this.y == point2.y;
        }
        return false;
    }
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
func isRectangleCover(rectangles [][]int) bool {
    type point struct{ x, y int }
    area, minX, minY, maxX, maxY := 0, rectangles[0][0], rectangles[0][1], rectangles[0][2], rectangles[0][3]
    cnt := map[point]int{}
    for _, rect := range rectangles {
        x, y, a, b := rect[0], rect[1], rect[2], rect[3]
        area += (a - x) * (b - y)

        minX = min(minX, x)
        minY = min(minY, y)
        maxX = max(maxX, a)
        maxY = max(maxY, b)

        cnt[point{x, y}]++
        cnt[point{x, b}]++
        cnt[point{a, y}]++
        cnt[point{a, b}]++
    }

    if area != (maxX-minX)*(maxY-minY) || cnt[point{minX, minY}] != 1 || cnt[point{minX, maxY}] != 1 || cnt[point{maxX, minY}] != 1 || cnt[point{maxX, maxY}] != 1 {
        return false
    }

    delete(cnt, point{minX, minY})
    delete(cnt, point{minX, maxY})
    delete(cnt, point{maxX, minY})
    delete(cnt, point{maxX, maxY})

    for _, c := range cnt {
        if c != 2 && c != 4 {
            return false
        }
    }
    return true
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

func max(a, b int) int {
    if b > a {
        return b
    }
    return a
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
typedef pair<int, int> Point;

class Solution {
public:
    bool isRectangleCover(vector<vector<int>>& rectangles) {
        long area = 0;
        int minX = rectangles[0][0], minY = rectangles[0][1], maxX = rectangles[0][2], maxY = rectangles[0][3];
        map<Point, int> cnt;
        for (auto & rect : rectangles) {
            int x = rect[0], y = rect[1], a = rect[2], b = rect[3];
            area += (long) (a - x) * (b - y);

            minX = min(minX, x);
            minY = min(minY, y);
            maxX = max(maxX, a);
            maxY = max(maxY, b);

            Point point1({x, y});
            Point point2({x, b});
            Point point3({a, y});
            Point point4({a, b});

            cnt[point1] += 1;
            cnt[point2] += 1;
            cnt[point3] += 1;
            cnt[point4] += 1;
        }

        Point pointMinMin({minX, minY});
        Point pointMinMax({minX, maxY});
        Point pointMaxMin({maxX, minY});
        Point pointMaxMax({maxX, maxY});
        if (area != (long long) (maxX - minX) * (maxY - minY) || !cnt.count(pointMinMin) || !cnt.count(pointMinMax) || !cnt.count(pointMaxMin) || !cnt.count(pointMaxMax)) {
            return false;
        }

        cnt.erase(pointMinMin);
        cnt.erase(pointMinMax);
        cnt.erase(pointMaxMin);
        cnt.erase(pointMaxMax);

        for (auto & entry : cnt) {
            int value = entry.second;
            if (value != 2 && value != 4) {
                return false;
            }
        }
        return true;
    }
};
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
var isRectangleCover = function(rectangles) {
    let area = 0;
    let minX = rectangles[0][0], minY = rectangles[0][1], maxX = rectangles[0][2], maxY = rectangles[0][3];
    const cnt = new Map();
    for (const rect of rectangles) {
        const x = rect[0], y = rect[1], a = rect[2], b = rect[3];
        area += (a - x) * (b - y);

        minX = Math.min(minX, x);
        minY = Math.min(minY, y);
        maxX = Math.max(maxX, a);
        maxY = Math.max(maxY, b);

        cnt.set([x, y].toString(), (cnt.get([x, y].toString()) || 0) + 1);
        cnt.set([x, b].toString(), (cnt.get([x, b].toString()) || 0) + 1);
        cnt.set([a, y].toString(), (cnt.get([a, y].toString()) || 0) + 1);
        cnt.set([a, b].toString(), (cnt.get([a, b].toString()) || 0) + 1);
    }
    
    const pointMinMin = [minX, minY].toString();
    const pointMinMax = [minX, maxY].toString();
    const pointMaxMin = [maxX, minY].toString();
    const pointMaxMax = [maxX, maxY].toString();
    if (area !== (maxX - minX) * (maxY - minY) || (cnt.get(pointMinMin) || 0) !== 1 || (cnt.get(pointMinMax) || 0) !== 1 || (cnt.get(pointMaxMin) || 0) !== 1 || (cnt.get(pointMaxMax) || 0) !== 1) {
        console.log(cnt.get([minX, minY].toString()))
        return false;
    }

    cnt.delete(pointMinMin);
    cnt.delete(pointMinMax);
    cnt.delete(pointMaxMin);
    cnt.delete(pointMaxMax);

    for (const [_, value] of cnt.entries()) {
        if (value !== 2 && value !== 4) {
            
            return false;
        }
    }
    
    return true;
};

复杂度分析

  • 时间复杂度：$O(n)$，其中 $n$ 是数组 rectangles 的长度。

  • 空间复杂度：$O(n)$。我们需要用哈希表存储矩形的顶点及其出现次数。

 Comments
On this page
0391-完美矩形