给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
**输入:** num1 = "11", num2 = "123"
**输出:** "134"
示例 2:
**输入:** num1 = "456", num2 = "77"
**输出:** "533"
示例 3:
**输入:** num1 = "0", num2 = "0"
**输出:** "0"
提示:
1 <= num1.length, num2.length <= 104num1 和num2 都只包含数字 0-9num1 和num2 都不包含任何前导零
方法一:模拟 思路与算法
本题我们只需要对两个大整数模拟「竖式加法」的过程。竖式加法就是我们平常学习生活中常用的对两个整数相加的方法,回想一下我们在纸上对两个整数相加的操作,是不是如下图将相同数位对齐,从低到高逐位相加,如果当前位和超过 $10$,则向高位进一位?因此我们只要将这个过程用代码写出来即可。
具体实现也不复杂,我们定义两个指针 $i$ 和 $j$ 分别指向 num}_1$ 和 num}_2$ 的末尾,即最低位,同时定义一个变量 add 维护当前是否有进位,然后从末尾到开头逐位相加即可。你可能会想两个数字位数不同怎么处理,这里我们统一在指针当前下标处于负数的时候返回 $0$,等价于对位数较短的数字进行了补零操作 ,这样就可以除去两个数字位数不同情况的处理,具体可以看下面的代码。
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 class Solution {public : string addStrings (string num1, string num2) { int i = num1.length () - 1 , j = num2.length () - 1 , add = 0 ; string ans = "" ; while (i >= 0 || j >= 0 || add != 0 ) { int x = i >= 0 ? num1[i] - '0' : 0 ; int y = j >= 0 ? num2[j] - '0' : 0 ; int result = x + y + add; ans.push_back ('0' + result % 10 ); add = result / 10 ; i -= 1 ; j -= 1 ; } reverse (ans.begin (), ans.end ()); return ans; } };
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution { public String addStrings (String num1, String num2) { int i = num1.length() - 1 , j = num2.length() - 1 , add = 0 ; StringBuffer ans = new StringBuffer (); while (i >= 0 || j >= 0 || add != 0 ) { int x = i >= 0 ? num1.charAt(i) - '0' : 0 ; int y = j >= 0 ? num2.charAt(j) - '0' : 0 ; int result = x + y + add; ans.append(result % 10 ); add = result / 10 ; i--; j--; } ans.reverse(); return ans.toString(); } }
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 func addStrings (num1 string , num2 string ) string { add := 0 ans := "" for i, j := len (num1) - 1 , len (num2) - 1 ; i >= 0 || j >= 0 || add != 0 ; i, j = i - 1 , j - 1 { var x, y int if i >= 0 { x = int (num1[i] - '0' ) } if j >= 0 { y = int (num2[j] - '0' ) } result := x + y + add ans = strconv.Itoa(result%10 ) + ans add = result / 10 } return ans }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 var addStrings = function (num1, num2 ) { let i = num1.length - 1 , j = num2.length - 1 , add = 0 ; const ans = []; while (i >= 0 || j >= 0 || add != 0 ) { const x = i >= 0 ? num1.charAt (i) - '0' : 0 ; const y = j >= 0 ? num2.charAt (j) - '0' : 0 ; const result = x + y + add; ans.push (result % 10 ); add = Math .floor (result / 10 ); i -= 1 ; j -= 1 ; } return ans.reverse ().join ('' ); };
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 char * addStrings (char * num1, char * num2) { int i = strlen (num1) - 1 , j = strlen (num2) - 1 , add = 0 ; char * ans = (char *)malloc (sizeof (char ) * (fmax(i, j) + 3 )); int len = 0 ; while (i >= 0 || j >= 0 || add != 0 ) { int x = i >= 0 ? num1[i] - '0' : 0 ; int y = j >= 0 ? num2[j] - '0' : 0 ; int result = x + y + add; ans[len++] = '0' + result % 10 ; add = result / 10 ; i--, j--; } for (int i = 0 ; 2 * i < len; i++) { int t = ans[i]; ans[i] = ans[len - i - 1 ], ans[len - i - 1 ] = t; } ans[len++] = 0 ; return ans; }
复杂度分析
时间复杂度:$O(\max(\textit{len}_1,\textit{len}_2))$,其中 len}_1=\textit{num}_1.\text{length,len}_2=\textit{num}_2.\text{length。竖式加法的次数取决于较大数的位数。
空间复杂度:$O(1)$。除答案外我们只需要常数空间存放若干变量。在 Java 解法中使用到了 StringBuffer,故 Java 解法的空间复杂度为 $O(n)$。
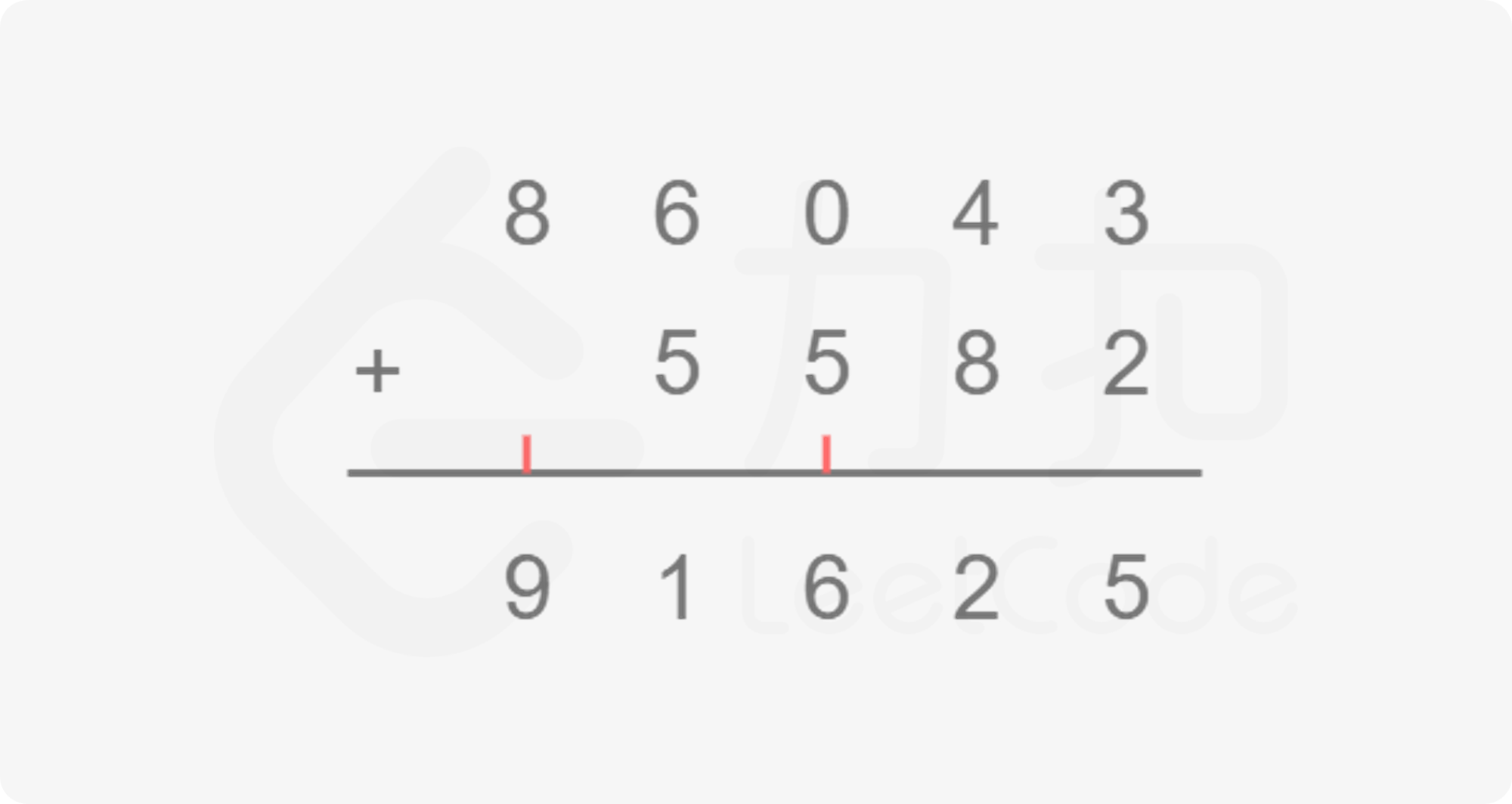 {:width=”50%”}
{:width=”50%”}