0424-替换后的最长重复字符
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
在执行上述操作后,返回包含相同字母的最长子字符串的长度。
示例 1:
**输入:** s = "ABAB", k = 2
**输出:** 4
**解释:** 用两个'A'替换为两个'B',反之亦然。
示例 2:
**输入:** s = "AABABBA", k = 1
**输出:** 4
**解释:**
将中间的一个'A'替换为'B',字符串变为 "AABBBBA"。
子串 "BBBB" 有最长重复字母, 答案为 4。
可能存在其他的方法来得到同样的结果。
提示:
1 <= s.length <= 105s仅由大写英文字母组成0 <= k <= s.length
📺 视频讲解
力扣君温馨小贴士:觉得视频时间长的扣友,可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看。
📖 文字解析
如果一个问题暂时没有思路,可以先考虑暴力解法(不一定要实现)。当前问题的暴力解法是:枚举输入字符串的 所有 子串,对于每一个子串:
- 如果子串里所有的字符都一样,就考虑长度更长的子串;
- 如果当前子串里出现了至少两种字符,要想使得替换以后所有的字符都一样,并且重复的、连续的部分更长,应该替换掉出现次数最多字符 以外 的字符。
暴力解法的时间复杂度为 $O(N^3)$(这里 $N$ 是输入字符串的长度,枚举所有子串 $O(N^2)$,对于每一个子串计算最多出现的字符 $O(N)$)。而题目的提示告诉我们字符串长度和 k 不会超过 $10^4$,暴力算法在这个数据规模下会超时。
暴力解法的缺点:
- 做了重复的工作,子串和子串有很多重合的部分,重复扫描它们是不划算的;
- 做了很多没有必要的工作:
- 如果找到了一个长度为
L且替换k个字符以后全部相等的子串,就没有必要考虑长度小于等于L的子串,因为题目只让我们找到符合题意的最长的长度; - 如果找到了一个长度为
L且替换k个字符以后不能全部相等的子串,左边界相同、长度更长的子串一定不符合要求(原因我们放在最后说)。
- 如果找到了一个长度为
优化暴力解法,我们须要研究一些典型的例子并结合题意找到思路。
以 s = AABCABBB,k = 2 为例,寻找替换 k 次以后字符全部相等的最长子串的长度的过程如下图所示:
< ,
,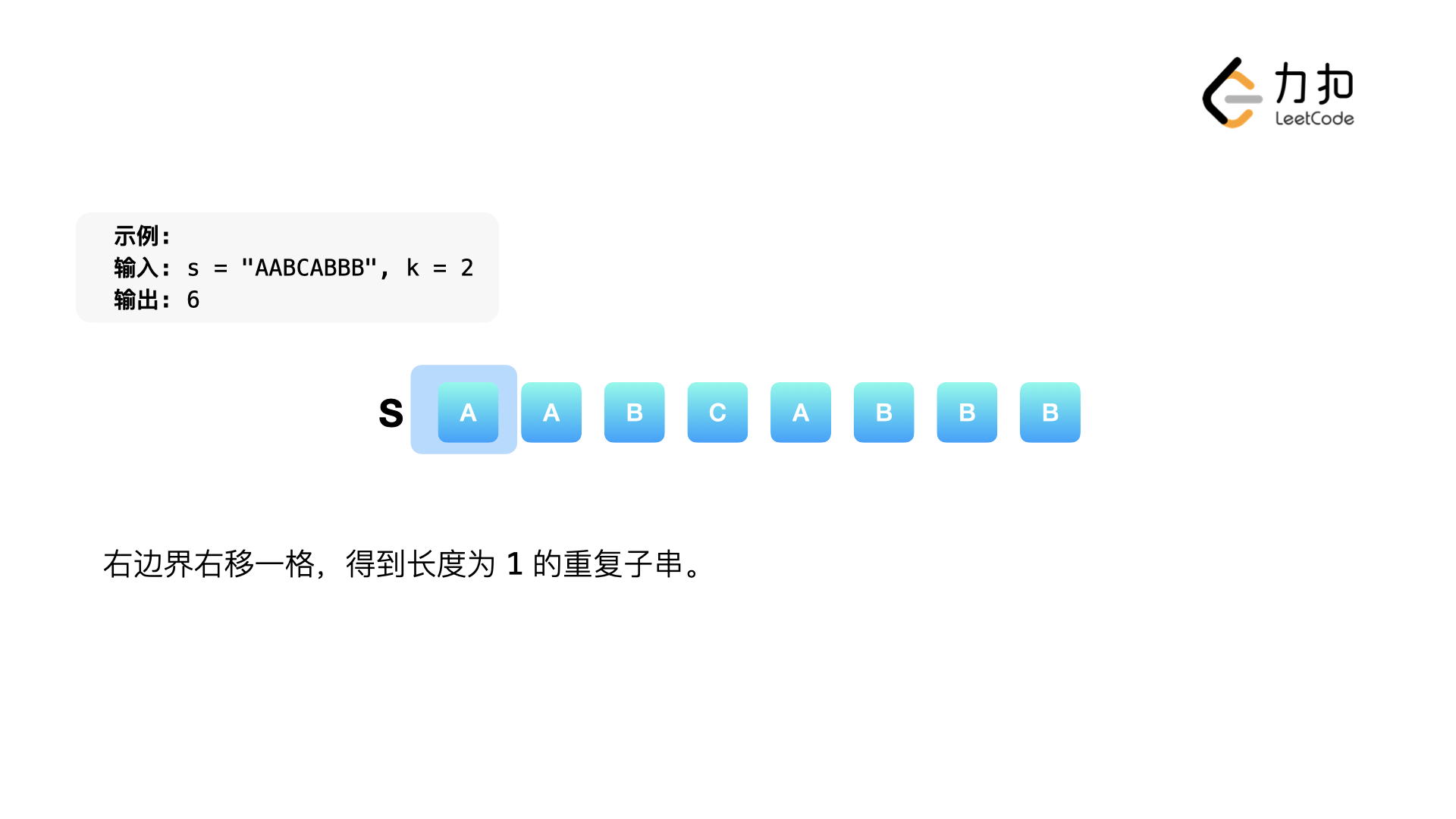 ,
,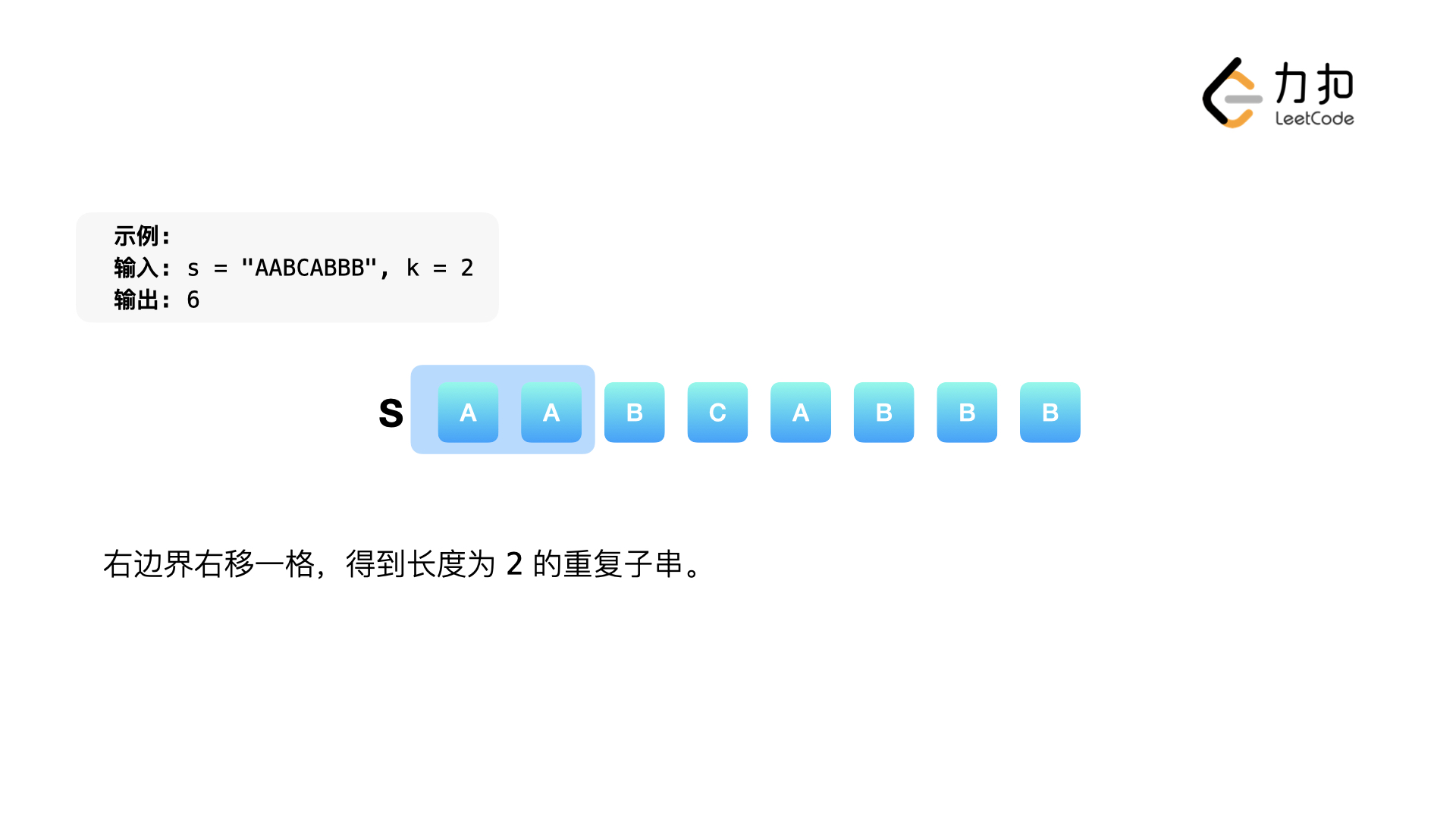 ,
, ,
, ,
,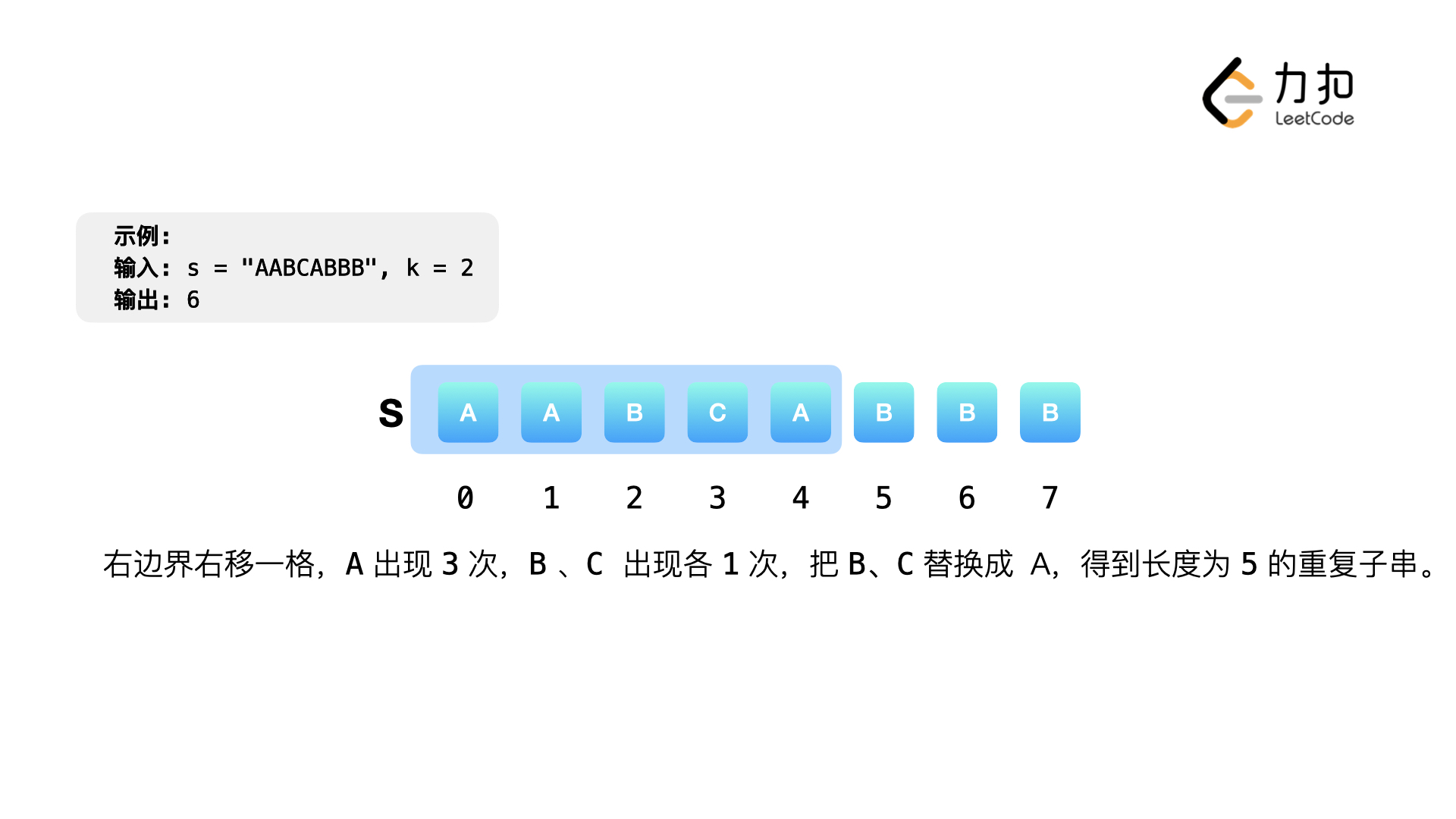 ,
, ,
, ,
, ,
, ,
, >
>
整个过程,我们使用了两个表示边界的变量,一前一后,交替在字符串上前进:右边界先向右和移动,直到它不能移动了为止,左边界再继续向右移动,整个过程像极了一个滑动的窗口在一条线段上移动。
我们还一直关心的是:考虑的子串中最多出现的字符是次数,因此须要一个频数数组,记录每个字符出现的次数。
方法:双指针(滑动窗口)
- 右边界先移动找到一个满足题意的可以替换
k个字符以后,所有字符都变成一样的当前看来最长的子串,直到右边界纳入一个字符以后,不能满足的时候停下; - 然后考虑左边界向右移动,左边界只须要向右移动一格以后,右边界就又可以开始向右移动了,继续尝试找到更长的目标子串;
- 替换后的最长重复子串就产生在右边界、左边界交替向右移动的过程中。
友情提示:建议大家先自己尝试编码实现,然后提交验证代码的正确性,并且思考清楚代码中的一些细节,相信会是一个非常不错的练习。
参考代码:
1 | public class Solution { |
复杂度分析:
- 时间复杂度:$O(N)$,这里 $N$ 是输入字符串
S的长度; - 空间复杂度:$O(A)$,这里 $A$ 是输入字符串
S出现的字符 ASCII 值的范围(感谢用户 @hyponarch 指正)。
以下是我们在编码的过程中思考的一些问题。我们建议大家先思考,通过调试,理解代码结果正确的原因。欢迎大家参与讨论。
1. 证明:如果长度为 L 的子串不符合题目的要求,那么左边界固定,长度更长的子串也不符合题目的要求。
答:记 $count(X)$ 表示长度为 L 的子串中,字符 X 出现的次数。
不失一般性,假设长度为 L 的子串,出现最多的字符为 A,记 $count(A) = x$。其余字符均为 B,记 $count(B) = y$。由字符 A 出现次数最多,可知 $x \ge y$。又由于长度为 L 的子串不符合题目的要求,可知 $y > k$。起点固定的情况下,考虑更长的子串:
- 如果接下来看到的字符都是
A(频数最多的字符越来越多),依然须要考虑把之前看到的B全部替换成为A,由于 $count(B) = y > k$,这是不能做到的; - 如果接下来看到的字符不是
A(频数较少的字符超过原来频数最多的字符),那么须要考虑把之前看到的A全部替换成为新的频数最多的字符,由于 $count(A) = x \ge y > k$,这也是不能做到的。
说明:这里我们只讨论了滑动窗口扫过的子区间只含有 2 种字符的情况,如果滑动窗口扫过的子区间只含有 3 种以及 3 种以上字符,讨论是类似的。
2. maxCount 在内层循环「左边界向右移动一个位置」的过程中,没有维护它的定义,结论是否正确?
答:结论依然正确。「左边界向右移动一个位置」的时候,maxCount 或者不变,或者值减 $1$。
maxCount的值虽然不维护,但数组freq的值是被正确维护的;- 当「左边界向右移动」之前:
- 如果有两种字符长度相等,左边界向右移动不改变
maxCount的值。例如s = [AAABBB]、k= 2,左边界A移除以后,窗口内字符出现次数不变,依然为 $3$; - 如果左边界移除以后,使得此时
maxCount的值变小,又由于 我们要找的只是最长替换k次以后重复子串的长度。接下来我们继续让右边界向右移动一格,有两种情况:① 右边界如果读到了刚才移出左边界的字符,恰好maxCount的值被正确维护;② 右边界如果读到了不是刚才移出左边界的字符,新的子串要想在符合题意的条件下变得更长,maxCount一定要比之前的值还要更多,因此不会错过更优的解。
- 如果有两种字符长度相等,左边界向右移动不改变
3. 内层循环里的 if 能不能改成 while?
答:可以但没有必要。理由依然是:我们只关心最长替换 k 次以后重复子串的长度。
- 正是因为多读了一个字符,使得
right - left > maxCount + k成立; - 在
left++以后,由于可以不维护maxCount的定义,right - left > maxCount + k不成立。因此if里面的代码块只会被执行一次。
4. 可以不用一直用 res 记录滑动窗口的最大长度,最后返回 right - left 即可。
答:依然是 我们只关心最长替换 k 次以后重复子串的长度,并且 maxCount 只会增加不会减少。在退出内层 if 语句的时候,区间 [left, right) 不一定是符合要求的子串,但是子串的长度一定等于题目要求的替换 k 次以后字符全都相等的最长子串(maxCount 的值不会变小,所以它会一直撑着滑动窗口的长度直到 right 遍历到字符串的末尾)。这一点如果很难理解的话,我们建议大家使用小测试数据、跟踪代码进行理解。
同类问题
- 「力扣」第 1004 题:最大连续 1 的个数 III ;
- 「力扣」第 1208 题:尽可能使字符串相等 ;
- 「力扣」第 1493 题:删掉一个元素以后全为 1 的最长子数组 。
「滑动窗口」是一类使用「双指针」技巧,通过两个变量在数组上同向交替移动解决问题的算法。这一类问题的思考路径通常是:先思考暴力解法,分析暴力解法的缺点(一般而言暴力解法的缺点是重复计算),然后 结合问题的特点,使用「双指针」技巧对暴力解法进行剪枝。因此,思考算法设计的合理性是更关键的,这一点适用于所有算法问题。
练习
- 「力扣」第 3 题:无重复字符的最长子串 ;
- 「力扣」第 209 题:长度最小的子数组 ;
- 「力扣」第 76 题:最小覆盖子串 ;
- 「力扣」第 438 题:找到字符串中所有字母异位词 ;
- 「力扣」第 567 题:字符串的排列 。
