0452-用最少数量的箭引爆气球

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为
x``start，x``end，且满足 xstart ≤ x ≤ x``end，则该气球会被引爆。可以射出的弓箭的数量
没有限制 。弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ， _返回引爆所有气球所必须射出的最小弓箭数 _。

示例 1：

**输入：** points = [[10,16],[2,8],[1,6],[7,12]]
**输出：** 2
**解释：** 气球可以用2支箭来爆破:
-在x = 6处射出箭，击破气球[2,8]和[1,6]。
-在x = 11处发射箭，击破气球[10,16]和[7,12]。

示例 2：

**输入：** points = [[1,2],[3,4],[5,6],[7,8]]
**输出：** 4
**解释：** 每个气球需要射出一支箭，总共需要4支箭。

示例 3：

**输入：** points = [[1,2],[2,3],[3,4],[4,5]]
**输出：** 2
解释：气球可以用2支箭来爆破:
- 在x = 2处发射箭，击破气球[1,2]和[2,3]。
- 在x = 4处射出箭，击破气球[3,4]和[4,5]。

提示:

1 <= points.length <= 105
points[i].length == 2
-231 <= xstart < xend <= 231 - 1

方法一：排序 + 贪心

思路与算法

我们首先随机地射出一支箭，再看一看是否能够调整这支箭地射出位置，使得我们可以引爆更多数目的气球。

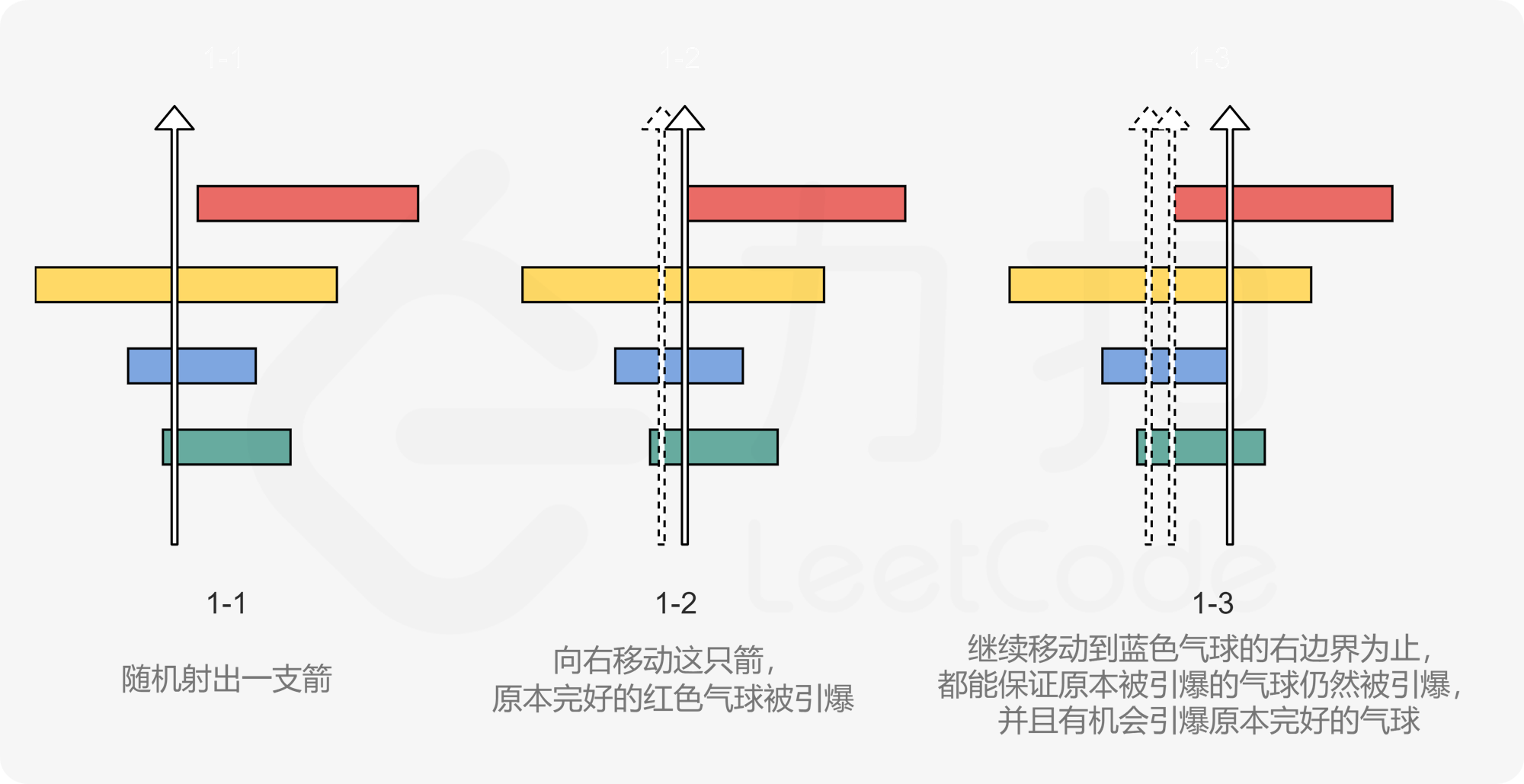
如图 1-1 所示，我们随机射出一支箭，引爆了除红色气球以外的所有气球。我们称所有引爆的气球为「原本引爆的气球」，其余的气球为「原本完好的气球」。可以发现，如果我们将这支箭的射出位置稍微往右移动一点，那么我们就有机会引爆红色气球，如图 1-2 所示。

那么我们最远可以将这支箭往右移动多远呢？我们唯一的要求就是：原本引爆的气球只要仍然被引爆就行了。这样一来，我们找出原本引爆的气球中右边界位置最靠左的那一个，将这支箭的射出位置移动到这个右边界位置，这也是最远可以往右移动到的位置：如图 1-3 所示，只要我们再往右移动一点点，这个气球就无法被引爆了。

为什么「原本引爆的气球仍然被引爆」是唯一的要求？别急，往下看就能看到其精妙所在。

因此，我们可以断定：

一定存在一种最优（射出的箭数最小）的方法，使得每一支箭的射出位置都恰好对应着某一个气球的右边界。

这是为什么？我们考虑任意一种最优的方法，对于其中的任意一支箭，我们都通过上面描述的方法，将这支箭的位置移动到它对应的「原本引爆的气球中最靠左的右边界位置」，那么这些原本引爆的气球仍然被引爆。这样一来，所有的气球仍然都会被引爆，并且每一支箭的射出位置都恰好位于某一个气球的右边界了。

有了这样一个有用的断定，我们就可以快速得到一种最优的方法了。考虑所有气球中右边界位置最靠左的那一个，那么一定有一支箭的射出位置就是它的右边界（否则就没有箭可以将其引爆了）。当我们确定了一支箭之后，我们就可以将这支箭引爆的所有气球移除，并从剩下未被引爆的气球中，再选择右边界位置最靠左的那一个，确定下一支箭，直到所有的气球都被引爆。

我们可以写出如下的伪代码：

let points := [[x(0), y(0)], [x(1), y(1)], ... [x(n-1), y(n-1)]]，表示 n 个气球
let burst := [false] * n，表示每个气球是否被引爆
let ans := 1，表示射出的箭数

将 points 按照 y 值（右边界）进行升序排序

while burst 中还有 false 值 do
    let i := 最小的满足 burst[i] = false 的索引 i
    for j := i to n-1 do
        if x(j) <= y(i) then
            burst[j] := true
        end if
    end for
end while

return ans

这样的做法在最坏情况下时间复杂度是 $O(n^2)$，即这 $n$ 个气球对应的区间互不重叠，while 循环需要执行 $n$ 次。那么我们如何继续进行优化呢？

事实上，在内层的 $j$ 循环中，当我们遇到第一个不满足 $x(j) \leq y(i)$ 的 $j$ 值，就可以直接跳出循环，并且这个 $y(j)$ 就是下一支箭的射出位置。为什么这样做是对的呢？我们考虑某一支箭的索引 $i_t$ 以及它的下一支箭的索引 $j_t$，对于索引在 $j_t$ 之后的任意一个可以被 $i_t$ 引爆的气球，记索引为 $j_0$，有：

$$
x(j_0) \leq y(i_t)
$$

由于 $y(i_t) \leq y(j_t)$ 显然成立，那么

$$
x(j_0) \leq y(j_t)
$$

也成立，也就是说：当前这支箭在索引 $j_t$（第一个无法引爆的气球）之后所有可以引爆的气球，下一支箭也都可以引爆。因此我们就证明了其正确性，也就可以写出如下的伪代码：

let points := [[x(0), y(0)], [x(1), y(1)], ... [x(n-1), y(n-1)]]，表示 n 个气球
let pos := y(0)，表示当前箭的射出位置
let ans := 1，表示射出的箭数

将 points 按照 y 值（右边界）进行升序排序

for i := 1 to n-1 do
    if x(i) > pos then
        ans := ans + 1
        pos := y(i)
    end if
end for

return ans

这样就可以将计算答案的时间从 $O(n^2)$ 降低至 $O(n)$。

代码

[sol1-C++]class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if (points.empty()) {
            return 0;
        }
        sort(points.begin(), points.end(), [](const vector<int>& u, const vector<int>& v) {
            return u[1] < v[1];
        });
        int pos = points[0][1];
        int ans = 1;
        for (const vector<int>& balloon: points) {
            if (balloon[0] > pos) {
                pos = balloon[1];
                ++ans;
            }
        }
        return ans;
    }
};

[sol1-Java]class Solution {
    public int findMinArrowShots(int[][] points) {
        if (points.length == 0) {
            return 0;
        }
        Arrays.sort(points, new Comparator<int[]>() {
            public int compare(int[] point1, int[] point2) {
                if (point1[1] > point2[1]) {
                    return 1;
                } else if (point1[1] < point2[1]) {
                    return -1;
                } else {
                    return 0;
                }
            }
        });
        int pos = points[0][1];
        int ans = 1;
        for (int[] balloon: points) {
            if (balloon[0] > pos) {
                pos = balloon[1];
                ++ans;
            }
        }
        return ans;
    }
}

[sol1-Python3]class Solution:
    def findMinArrowShots(self, points: List[List[int]]) -> int:
        if not points:
            return 0
        
        points.sort(key=lambda balloon: balloon[1])
        pos = points[0][1]
        ans = 1
        for balloon in points:
            if balloon[0] > pos:
                pos = balloon[1]
                ans += 1
        
        return ans

[sol1-JavaScript]var findMinArrowShots = function(points) {
    if (!points.length ) {
        return 0;
    }

    points.sort((a, b) => a[1] - b[1]);
    let pos = points[0][1]
    let ans = 1;
    for (let balloon of points) {
        if (balloon[0] > pos) {
            pos = balloon[1];
            ans++;
        }
    }
    return ans;
};

[sol1-Golang]func findMinArrowShots(points [][]int) int {
    if len(points) == 0 {
        return 0
    }
    sort.Slice(points, func(i, j int) bool { return points[i][1] < points[j][1] })
    maxRight := points[0][1]
    ans := 1
    for _, p := range points {
        if p[0] > maxRight {
            maxRight = p[1]
            ans++
        }
    }
    return ans
}

[sol1-C]int cmp(void* _a, void* _b) {
    int *a = *(int**)_a, *b = *(int**)_b;
    return a[1] < b[1] ? -1 : 1;
}

int findMinArrowShots(int** points, int pointsSize, int* pointsColSize) {
    if (!pointsSize) {
        return 0;
    }
    qsort(points, pointsSize, sizeof(int*), cmp);
    int pos = points[0][1];
    int ans = 1;
    for (int i = 0; i < pointsSize; ++i) {
        if (points[i][0] > pos) {
            pos = points[i][1];
            ++ans;
        }
    }
    return ans;
}

复杂度分析

时间复杂度：$O(n\log n)$，其中 $n$ 是数组 points 的长度。排序的时间复杂度为 $O(n \log n)$，对所有气球进行遍历并计算答案的时间复杂度为 $O(n)$，其在渐进意义下小于前者，因此可以忽略。
空间复杂度：$O(\log n)$，即为排序需要使用的栈空间。

结语

这道题的标记包含「贪心」，但本篇题解正文全文没有使用「贪心」二字，那么「贪心」的思想到底体现在哪里呢？欢迎读者评论区留言说出想法。