0461-汉明距离
两个整数之间的
汉明距离
指的是这两个数字对应二进制位不同的位置的数目。
给你两个整数 x 和 y,计算并返回它们之间的汉明距离。
示例 1:
**输入:** x = 1, y = 4
**输出:** 2
**解释:**
1 (0 0 0 1)
4 (0 1 0 0)
↑ ↑
上面的箭头指出了对应二进制位不同的位置。
示例 2:
**输入:** x = 3, y = 1
**输出:** 1
提示:
0 <= x, y <= 231 - 1
前言
汉明距离广泛应用于多个领域。在编码理论中用于错误检测,在信息论中量化字符串之间的差异。
两个整数之间的汉明距离是对应位置上数字不同的位数。
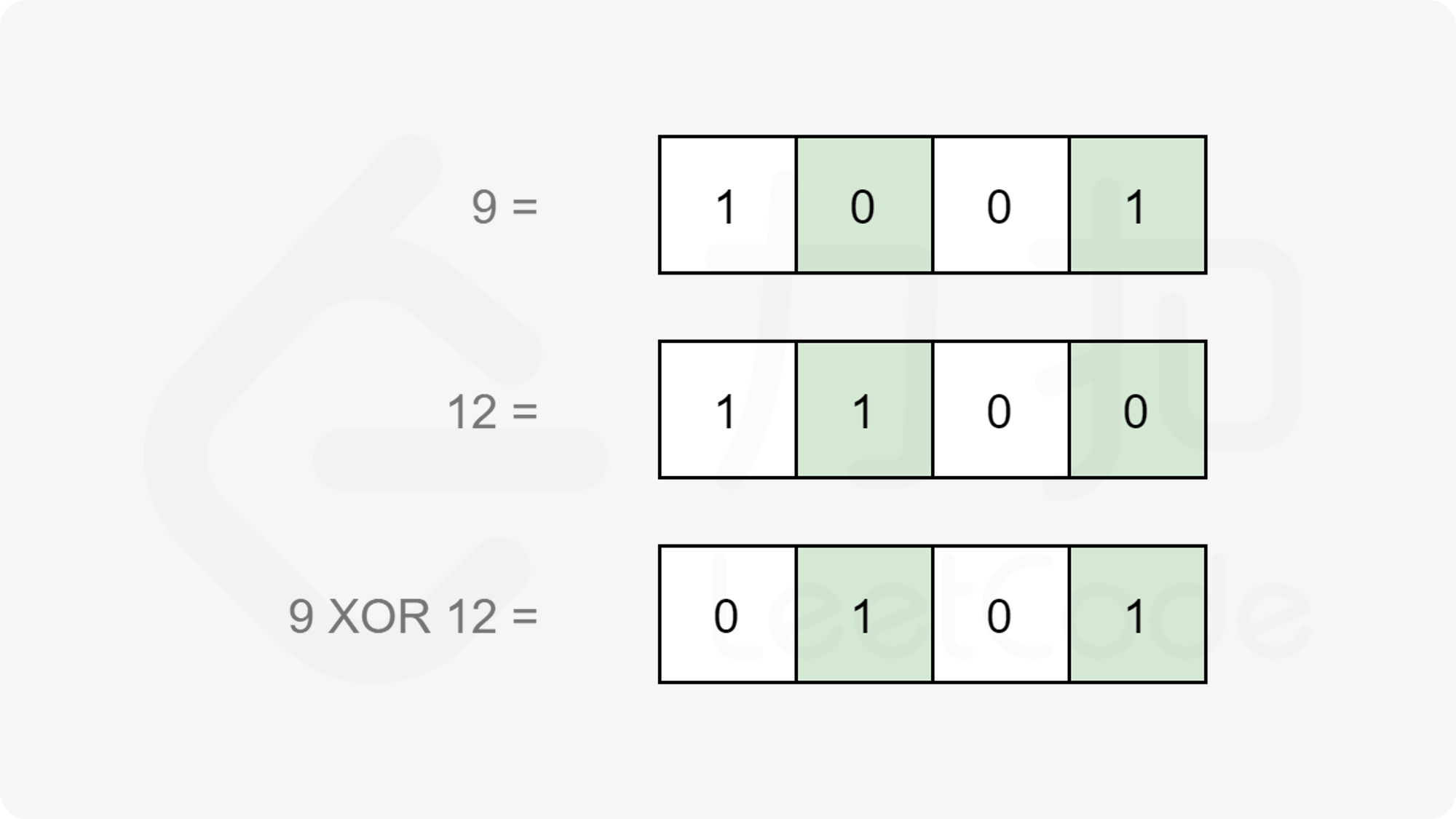
根据以上定义,我们使用异或运算,记为 $\oplus$,当且仅当输入位不同时输出为 $1$。
 {:width=”80%”}
{:width=”80%”}
计算 $x$ 和 $y$ 之间的汉明距离,可以先计算 $x \oplus y$,然后统计结果中等于 $1$ 的位数。
现在,原始问题转换为位计数问题。位计数有多种思路,将在下面的方法中介绍。
方法一:内置位计数功能
思路及算法
大多数编程语言都内置了计算二进制表达中 $1$ 的数量的函数。在工程中,我们应该直接使用内置函数。
代码
1 | class Solution { |
1 | class Solution { |
1 | func hammingDistance(x, y int) int { |
1 | int hammingDistance(int x, int y) { |
复杂度分析
时间复杂度:$O(1)$。不同语言的实现方法不一,我们可以近似认为其时间复杂度为 $O(1)$。
空间复杂度:$O(1)$。
方法二:移位实现位计数
思路及算法
在锻炼算法能力时,重复造轮子是不可避免的,也是应当的。因此读者们也需要尝试使用各种方法自己实现几个具有位计数功能的函数。本方法将使用位运算中移位的操作实现位计数功能。
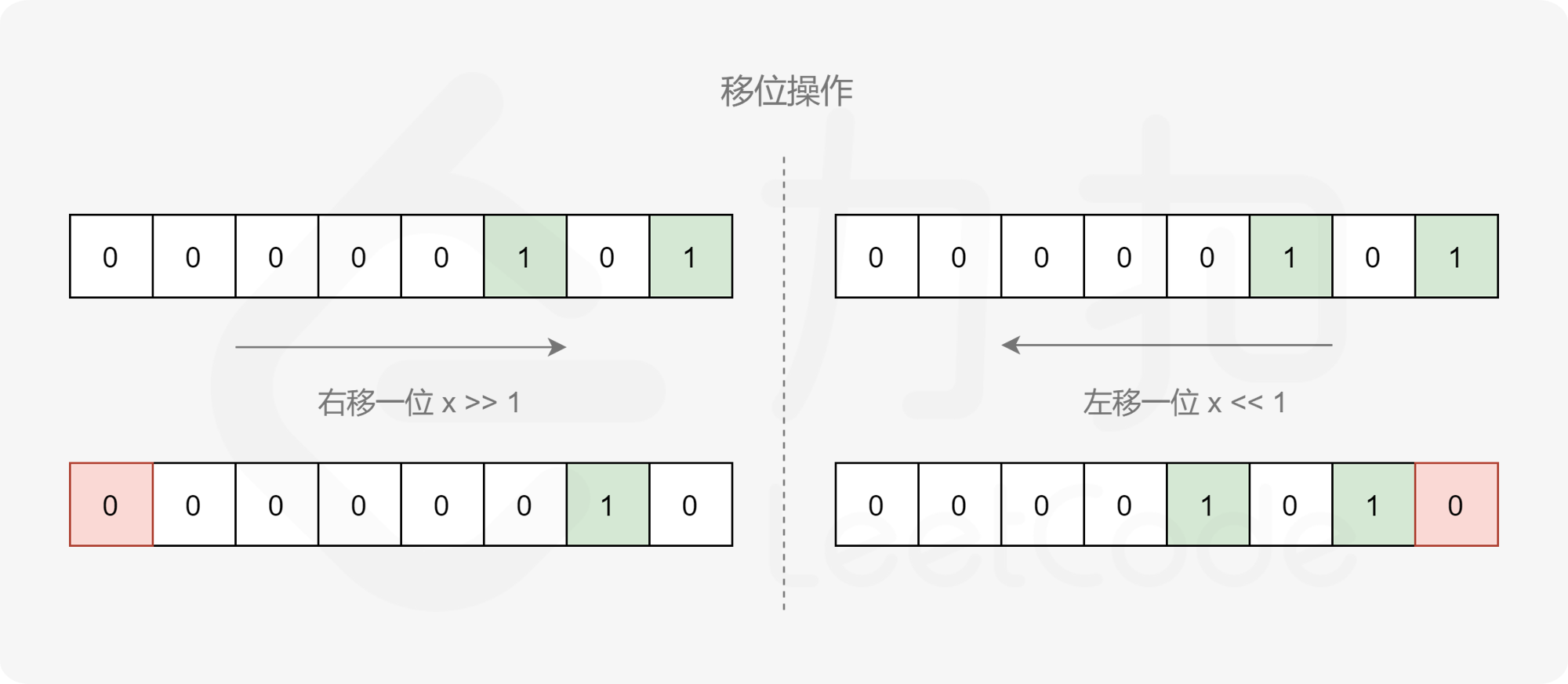
具体地,记 $s = x \oplus y$,我们可以不断地检查 $s$ 的最低位,如果最低位为 $1$,那么令计数器加一,然后我们令 $s$ 整体右移一位,这样 $s$ 的最低位将被舍去,原本的次低位就变成了新的最低位。我们重复这个过程直到 $s=0$ 为止。这样计数器中就累计了 $s$ 的二进制表示中 $1$ 的数量。
代码
1 | class Solution { |
1 | class Solution { |
1 | public class Solution { |
1 | var hammingDistance = function(x, y) { |
1 | func hammingDistance(x, y int) (ans int) { |
1 | int hammingDistance(int x, int y) { |
复杂度分析
时间复杂度:$O(\log C)$,其中 $C$ 是元素的数据范围,在本题中 $\log C=\log 2^{31} = 31$。
空间复杂度:$O(1)$。
方法三:Brian Kernighan 算法
思路及算法
在方法二中,对于 $s=(10001100)_2$ 的情况,我们需要循环右移 $8$ 次才能得到答案。而实际上如果我们可以跳过两个 $1$ 之间的 $0$,直接对 $1$ 进行计数,那么就只需要循环 $3$ 次即可。
我们可以使用 Brian Kernighan 算法进行优化,具体地,该算法可以被描述为这样一个结论:记 $f(x)$ 表示 $x$ 和 $x-1$ 进行与运算所得的结果(即 $f(x)=x&(x-1)$),那么 $f(x)$ 恰为 $x$ 删去其二进制表示中最右侧的 $1$ 的结果。
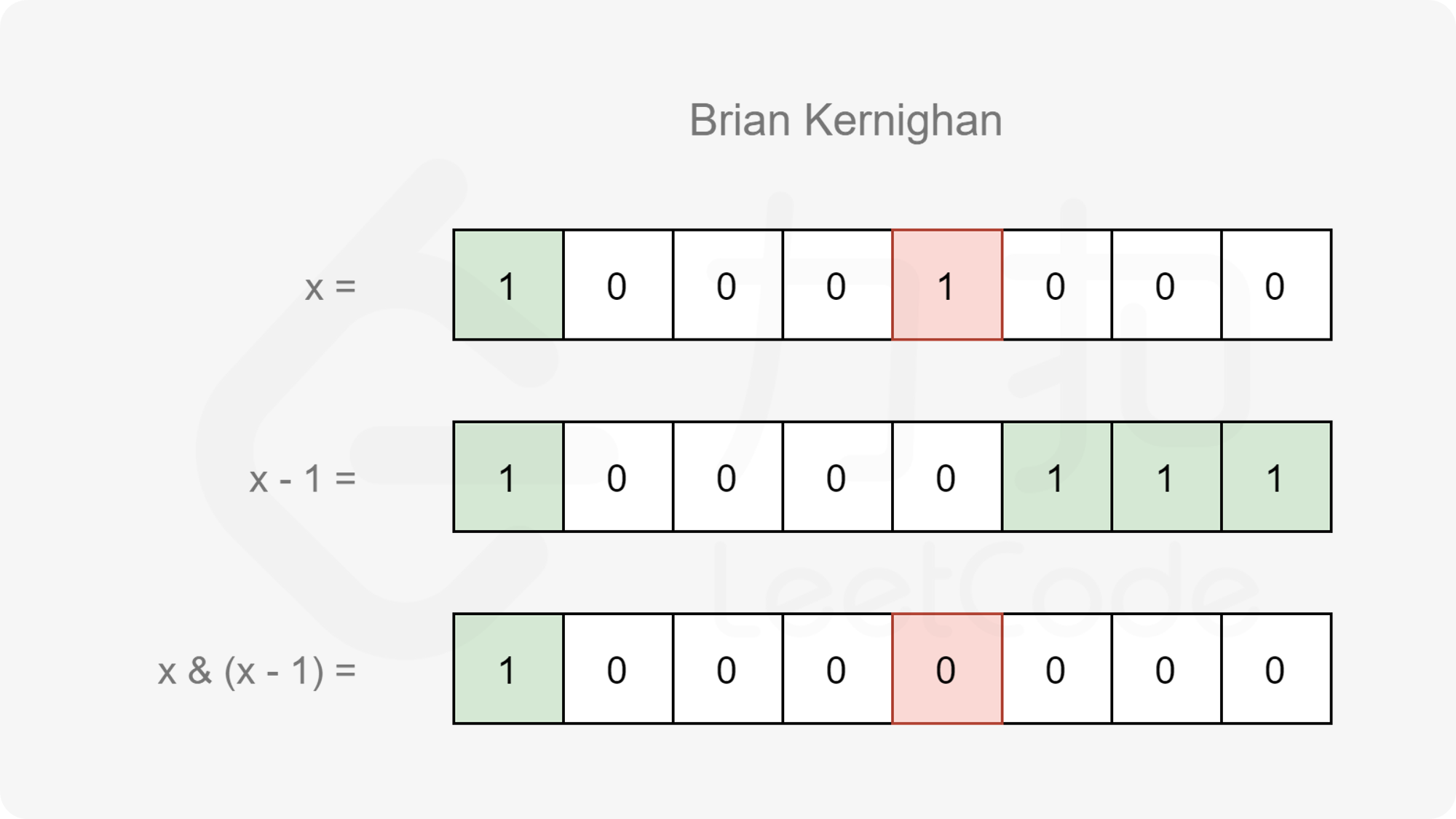
基于该算法,当我们计算出 $s = x \oplus y$,只需要不断让 $s = f(s)$,直到 $s=0$ 即可。这样每循环一次,$s$ 都会删去其二进制表示中最右侧的 $1$,最终循环的次数即为 $s$ 的二进制表示中 $1$ 的数量。
注意
Brian Kernighan 算法发布在 $1988$ 年出版的 The C Programming Language (Second Edition) 的练习中(由 Brian W. Kernighan 和 Dennis M. Ritchie 编写),但是 Donald Knuth 在 $2006$ 年 $4$ 月 $19$ 日指出,该方法第一次是由 Peter Wegner 在 $1960$ 年的 CACM3 上出版。可以在上述书籍中找到更多位操作的技巧。
代码
1 | class Solution { |
1 | class Solution { |
1 | public class Solution { |
1 | var hammingDistance = function(x, y) { |
1 | func hammingDistance(x, y int) (ans int) { |
1 | int hammingDistance(int x, int y) { |
复杂度分析
时间复杂度:$O(\log C)$,其中 $C$ 是元素的数据范围,在本题中 $\log C=\log 2^{31} = 31$。
空间复杂度:$O(1)$。
✨扣友帮帮团 - 互动答疑
即日起 - 5 月 30 日,点击 这里 前往「扣友帮帮团 」活动页,把你遇到的问题大胆地提出来,让扣友为你解答~
🎁 奖励规则
被采纳数量排名 1~3 名:「力扣极客套装」 *1 并将获得「力扣神秘应援团」内测资格
被采纳数量排名 4~10 名:「力扣鼠标垫」 *1 并将获得「力扣神秘应援团」内测资格
「诲人不倦」:活动期间「解惑者」只要有 1 个回答被采纳,即可获得 20 LeetCoins 奖励!
「求知若渴」:活动期间「求知者」在活动页发起一次符合要求的疑问帖并至少采纳一次「解惑者」的回答,即可获得 20 LeetCoins 奖励!
活动详情猛戳链接了解更多:🐞 你有 BUG 我来帮 - 力扣互动答疑季
 {:width=260px}
{:width=260px}