0478-在圆内随机生成点

给定圆的半径和圆心的位置，实现函数 randPoint ，在圆中产生均匀随机点。

实现 Solution 类:

• Solution(double radius, double x_center, double y_center) 用圆的半径 radius 和圆心的位置 (x_center, y_center) 初始化对象
• randPoint() 返回圆内的一个随机点。圆周上的一点被认为在圆内。答案作为数组返回 [x, y] 。

示例 1：

**输入:** ["Solution","randPoint","randPoint","randPoint"]
[[1.0, 0.0, 0.0], [], [], []]
**输出:** [null, [-0.02493, -0.38077], [0.82314, 0.38945], [0.36572, 0.17248]]
**解释:**
Solution solution = new Solution(1.0, 0.0, 0.0);
solution.randPoint ();//返回[-0.02493，-0.38077]
solution.randPoint ();//返回[0.82314,0.38945]
solution.randPoint ();//返回[0.36572,0.17248]

提示：

• 0 < radius <= 108
• -107 <= x_center, y_center <= 107
• randPoint 最多被调用 3 * 104 次

前言

下面的所有方法基于假设：语言提供的生成浮点数的 API 得到的结果是均匀的。

事实上，根据 IEEE 754 ，只有有限个浮点数能被有效表示，并且浮点数的绝对值越大，密度就越低。这说明我们并不能生成均匀的随机浮点数。

但「如何均匀生成随机浮点数」显然不是本题的重点。我们可以假设语言提供了一个 API，它给定两个浮点数 l, r，可以生成区间 [l, r) 中的均匀的随机浮点数。我们需要使用这个 API 来完成题目的要求。

方法一：拒绝采样

思路与算法

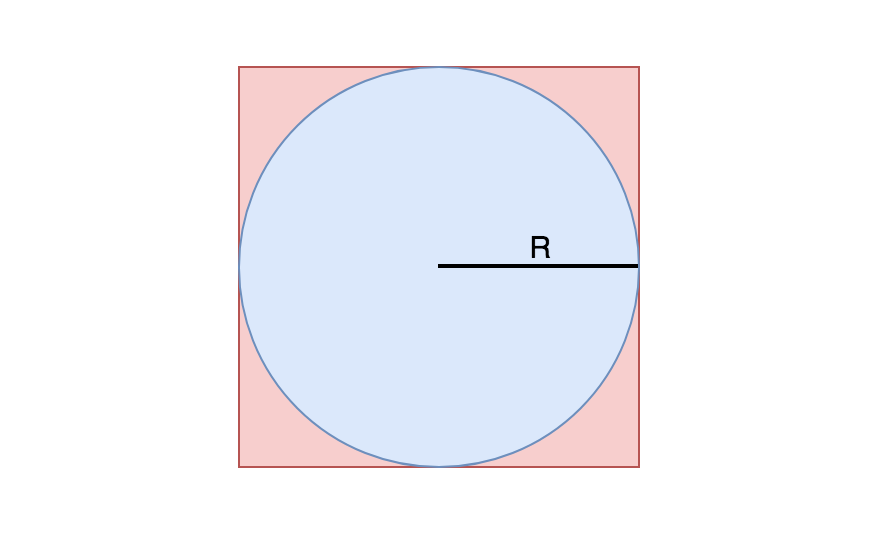
拒绝采样的意思是说：我们在一个更大的范围内生成随机数，并拒绝掉那些不在题目给定范围内的随机数，此时保留下来的随机数都是在范围内的。为了在一个半径为 R 的圆中生成均匀随机点，我们可以使用一个边长为 2R 的正方形覆盖住圆，并在正方形内生成均匀随机点，此时就只需要对于横坐标和纵坐标分别生成一个随机数即可。

{:width=300px}

若该点落在圆内，我们就返回这个点，否则我们拒绝这个点，重新生成，直到新的随机点落在圆内。

细节

由于正方形的面积为 (2R)^2 = 4R^2，圆的面积为 \pi R^2，因此在正方形中随机生成的点，落在圆内的概率为 Pr}(\cdot) = \dfrac{\pi R^2}{4R^2} \approx 0.785，期望的生成次数为 E}(\cdot) = \dfrac{1}{0.785} \approx 1.274 = O(1)。

在正方形中生成点时（正方形中心的坐标简记为原点），如果我们在 [-R, R) 的范围内生成随机数，那么是无法生成到横坐标或纵坐标恰好为 R 的点，对应到圆上时，会有圆周上与正方形边相切的两个点无法随机到。我们可以在生成时稍微提高右边界（例如 2R + \epsilon，其中 \epsilon 是一个很小的常数，例如 10^{-7），或者直接忽略这两个点，因为它们的勒贝格测度为零。

代码

[sol1-C++]

class Solution {
private:
    mt19937 gen{random_device{}()};
    uniform_real_distribution<double> dis;
    double xc, yc, r;

public:
    Solution(double radius, double x_center, double y_center): dis(-radius, radius), xc(x_center), yc(y_center), r(radius) {}
    
    vector<double> randPoint() {
        while (true) {
            double x = dis(gen), y = dis(gen);
            if (x * x + y * y <= r * r) {
                return {xc + x, yc + y};
            }
        }
    }
};

[sol1-Java]

class Solution {
    Random random;
    double xc, yc, r;

    public Solution(double radius, double x_center, double y_center) {
        random = new Random();
        xc = x_center;
        yc = y_center;
        r = radius;
    }
    
    public double[] randPoint() {
        while (true) {
            double x = random.nextDouble() * (2 * r) - r;
            double y = random.nextDouble() * (2 * r) - r;
            if (x * x + y * y <= r * r) {
                return new double[]{xc + x, yc + y};
            }
        }
    }
}

[sol1-C#]

public class Solution {
    Random random;
    double xc, yc, r;

    public Solution(double radius, double x_center, double y_center) {
        random = new Random();
        xc = x_center;
        yc = y_center;
        r = radius;
    }
    
    public double[] RandPoint() {
        while (true) {
            double x = random.NextDouble() * (2 * r) - r;
            double y = random.NextDouble() * (2 * r) - r;
            if (x * x + y * y <= r * r) {
                return new double[]{xc + x, yc + y};
            }
        }
    }
}

[sol1-Python3]

class Solution:

    def __init__(self, radius: float, x_center: float, y_center: float):
        self.xc = x_center
        self.yc = y_center
        self.r = radius

    def randPoint(self) -> List[float]:
        while True:
            x, y = random.uniform(-self.r, self.r), random.uniform(-self.r, self.r)
            if x * x + y * y <= self.r * self.r:
                return [self.xc + x, self.yc + y]

[sol1-C]

typedef struct {
    double radius;
    double x_center;
    double y_center;
} Solution;

Solution* solutionCreate(double radius, double x_center, double y_center) {
    srand((unsigned)time(NULL));
    Solution *obj = (Solution *)malloc(sizeof(Solution));
    obj->radius = radius;
    obj->x_center = x_center;
    obj->y_center = y_center;
    return obj;
}

double* solutionRandPoint(Solution* obj, int* retSize) {
    double r = obj->radius;
    double *res = (double *)malloc(sizeof(double) * 2);
    while (true) {
        double x = (double)rand() / RAND_MAX * (2 * r) - r;
        double y = (double)rand() / RAND_MAX * (2 * r) - r;
        if (x * x + y * y <= r * r) {
            res[0] = x + obj->x_center;
            res[1] = y + obj->y_center;
            *retSize = 2;
            return res;
        }
    }
}

void solutionFree(Solution* obj) {
    free(obj);
}

[sol1-Golang]

type Solution struct {
    radius, xCenter, yCenter float64
}

func Constructor(radius, xCenter, yCenter float64) Solution {
    return Solution{radius, xCenter, yCenter}
}

func (s *Solution) RandPoint() []float64 {
    for {
        x := rand.Float64()*2 - 1
        y := rand.Float64()*2 - 1 // [-1,1) 的随机数
        if x*x+y*y < 1 {
            return []float64{s.xCenter + x*s.radius, s.yCenter + y*s.radius}
        }
    }
}

[sol1-JavaScript]

var Solution = function(radius, x_center, y_center) {
    this.xc = x_center;
    this.yc = y_center;
    this.r = radius;
};

Solution.prototype.randPoint = function() {
    while (true) {
        const x = Math.random() * (2 * this.r) - this.r;
        const y = Math.random() * (2 * this.r) - this.r;
        if (x * x + y * y <= this.r * this.r) {
            return [this.xc + x, this.yc + y];
        }
    }
};

复杂度分析

• 时间复杂度：期望时间复杂度为 O(1)。

• 空间复杂度：O(1)。

方法二：计算分布函数

思路与算法

本方法需要一定的概率论知识，尤其是「概率密度函数 PDF」以及「累积分布函数 CDF」。

不失一般性，我们只考虑在原点且半径为 1 的单位圆。对于非一般性的情况，我们只需要把生成的点的坐标根据半径等比例放大，再根据圆心坐标进行平移即可。

对于两条线段，我们在它们中均匀随机生成点。如果一条线段的长度是另一条的两倍，那么生成的点在第一条线段上的概率也应当是在第二条线段上的概率的两倍。因此我们考虑单位圆内部的每一个圆环，生成的点落在半径为 R_1 的圆环上的概率应当与圆环的周长成正比，同时也与 R_1 成正比，即 f(R_1) = k \cdot R_1，其中 f(r) 为概率密度函数 PDF。由于 f(x) 在定义域上的积分为 1，因此：

1 = \int_0^1 k \cdot r ~\mathrm{d}r = \left.1}{2}k \cdot r^2 \right|^1_0 = 1}{2} k

解得 k=2，即 f(r) = 2r。

得到了概率密度函数后，我们计算累积分布函数 CDF，即：

F(r) = \int_0^r f(t) ~\mathrm{d}t = r^2

累积分布函数 F(r) 告诉我们，在单位圆中随机生成一个点，它离圆心的距离小于等于 r 的概率为 F(r) = r^2。对于一个给定的累计分布函数，如果我们想要根据其生成随机变量，可以通过 [0, 1) 的均匀分布生成随机变量 u，找到满足 F(r) = u 的 r，此时 r 即为满足累计分布函数的随机变量。

从 F(r) = u 以及 F(r) 单调递增可以得到 r = F^{-1}(u)。由于 F(r) = r^2，因此 r = F^{-1}(u) = \sqrt{u，即用 r = \sqrt{u 来生成随机变量 r。

除了 r 之外，我们还需要随机生成其与水平轴正方向的夹角 \theta \in [0, 2\pi)，随后我们就可以根据：

\begin{cases}
\text{x} = r \cdot \cos \theta \
\text{y} = r \cdot \sin \theta
\end{cases}

得到点在单位圆内的坐标。再经过等比例放大坐标和平移两个步骤，就可以得到任意圆内的一个均匀随机生成的点了。

细节

注意如果直接在 [0, 1) 范围内生成 r 以及 [0, 2\pi) 范围内生成 \theta，得到的随机点是不均匀的，可以通过任意一种可视化工具观察结果。

[sol2-C++]

class Solution {
private:
    mt19937 gen{random_device{}()};
    uniform_real_distribution<double> dis;
    double xc, yc, r;

public:
    Solution(double radius, double x_center, double y_center): dis(0, 1), xc(x_center), yc(y_center), r(radius) {}
    
    vector<double> randPoint() {
        double u = dis(gen), theta = dis(gen) * 2 * acos(-1.0);
        double r = sqrt(u);
        return {xc + r * cos(theta) * this->r, yc + r * sin(theta) * this->r};
    }
};

[sol2-Java]

class Solution {
    Random random;
    double xc, yc, r;

    public Solution(double radius, double x_center, double y_center) {
        random = new Random();
        xc = x_center;
        yc = y_center;
        r = radius;
    }
    
    public double[] randPoint() {
        double u = random.nextDouble();
        double theta = random.nextDouble() * 2 * Math.PI;
        double r = Math.sqrt(u);
        return new double[]{xc + r * Math.cos(theta) * this.r, yc + r * Math.sin(theta) * this.r};
    }
}

[sol2-C#]

public class Solution {
    Random random;
    double xc, yc, r;

    public Solution(double radius, double x_center, double y_center) {
        random = new Random();
        xc = x_center;
        yc = y_center;
        r = radius;
    }
    
    public double[] RandPoint() {
        double u = random.NextDouble();
        double theta = random.NextDouble() * 2 * Math.PI;
        double r = Math.Sqrt(u);
        return new double[]{xc + r * Math.Cos(theta) * this.r, yc + r * Math.Sin(theta) * this.r};
    }
}

[sol2-Python3]

class Solution:

    def __init__(self, radius: float, x_center: float, y_center: float):
        self.xc = x_center
        self.yc = y_center
        self.r = radius

    def randPoint(self) -> List[float]:
        u, theta = random.random(), random.random() * 2 * math.pi
        r = sqrt(u)
        return [self.xc + r * math.cos(theta) * self.r, self.yc + r * math.sin(theta) * self.r]

[sol2-C]

typedef struct {
    double radius;
    double x_center;
    double y_center;
} Solution;

Solution* solutionCreate(double radius, double x_center, double y_center) {
    srand((unsigned)time(NULL));
    Solution *obj = (Solution *)malloc(sizeof(Solution));
    obj->radius = radius;
    obj->x_center = x_center;
    obj->y_center = y_center;
    return obj;
}

double* solutionRandPoint(Solution* obj, int* retSize) {
    double u = (double)rand() / RAND_MAX;
    double theta = (double)rand() / RAND_MAX * 2 * M_PI;
    double r = sqrt(u);
    double *res = (double *)malloc(sizeof(double) * 2);
    res[0] = obj->x_center + r * cos(theta) * obj->radius;
    res[1] = obj->y_center + r * sin(theta) * obj->radius;
    *retSize = 2;
    return res;
}

void solutionFree(Solution* obj) {
    free(obj);
}

[sol2-Golang]

type Solution struct {
    radius, xCenter, yCenter float64
}

func Constructor(radius, xCenter, yCenter float64) Solution {
    return Solution{radius, xCenter, yCenter}
}

func (s *Solution) RandPoint() []float64 {
    r := math.Sqrt(rand.Float64())
    sin, cos := math.Sincos(rand.Float64() * 2 * math.Pi)
    return []float64{s.xCenter + r*cos*s.radius, s.yCenter + r*sin*s.radius}
}

[sol2-JavaScript]

var Solution = function(radius, x_center, y_center) {
    this.xc = x_center;
    this.yc = y_center;
    this.r = radius;
};

Solution.prototype.randPoint = function() {
    const u = Math.random();
    const theta = Math.random() * 2 * Math.PI;
    const r = Math.sqrt(u);
    return [this.xc + r * Math.cos(theta) * this.r, this.yc + r * Math.sin(theta) * this.r];
};

复杂度分析

• 时间复杂度：O(1)。

• 空间复杂度：O(1)。