0508-出现次数最多的子树元素和

给你一个二叉树的根结点 root ，请返回出现次数最多的子树元素和。如果有多个元素出现的次数相同，返回所有出现次数最多的子树元素和（不限顺序）。

一个结点的 「子树元素和」 定义为以该结点为根的二叉树上所有结点的元素之和（包括结点本身）。

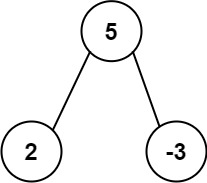
示例 1：

**输入:** root = [5,2,-3]
**输出:** [2,-3,4]

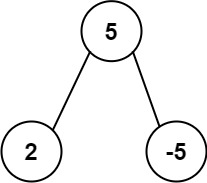
示例 2：

**输入:** root = [5,2,-5]
**输出:** [2]

提示:

• 节点数在 [1, 104] 范围内
• -105 <= Node.val <= 105

方法一：深度优先搜索

我们可以从根结点出发，深度优先搜索这棵二叉树。对于每棵子树，其子树元素和等于子树根结点的元素值，加上左子树的元素和，以及右子树的元素和。

用哈希表统计每棵子树的元素和的出现次数，计算出现次数的最大值 maxCnt，最后将出现次数等于 maxCnt 的所有元素和返回。

[sol1-Python3]

class Solution:
    def findFrequentTreeSum(self, root: TreeNode) -> List[int]:
        cnt = Counter()
        def dfs(node: TreeNode) -> int:
            if node is None:
                return 0
            sum = node.val + dfs(node.left) + dfs(node.right)
            cnt[sum] += 1
            return sum
        dfs(root)

        maxCnt = max(cnt.values())
        return [s for s, c in cnt.items() if c == maxCnt]

[sol1-C++]

class Solution {
    unordered_map<int, int> cnt;
    int maxCnt = 0;

    int dfs(TreeNode *node) {
        if (node == nullptr) {
            return 0;
        }
        int sum = node->val + dfs(node->left) + dfs(node->right);
        maxCnt = max(maxCnt, ++cnt[sum]);
        return sum;
    }

public:
    vector<int> findFrequentTreeSum(TreeNode *root) {
        dfs(root);
        vector<int> ans;
        for (auto &[s, c]: cnt) {
            if (c == maxCnt) {
                ans.emplace_back(s);
            }
        }
        return ans;
    }
};

[sol1-Java]

class Solution {
    Map<Integer, Integer> cnt = new HashMap<Integer, Integer>();
    int maxCnt = 0;

    public int[] findFrequentTreeSum(TreeNode root) {
        dfs(root);
        List<Integer> list = new ArrayList<Integer>();
        for (Map.Entry<Integer, Integer> entry : cnt.entrySet()) {
            int s = entry.getKey(), c = entry.getValue();
            if (c == maxCnt) {
                list.add(s);
            }
        }
        int[] ans = new int[list.size()];
        for (int i = 0; i < list.size(); ++i) {
            ans[i] = list.get(i);
        }
        return ans;
    }

    public int dfs(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int sum = node.val + dfs(node.left) + dfs(node.right);
        cnt.put(sum, cnt.getOrDefault(sum, 0) + 1);
        maxCnt = Math.max(maxCnt, cnt.get(sum));
        return sum;
    }
}

[sol1-C#]

public class Solution {
    Dictionary<int, int> cnt = new Dictionary<int, int>();
    int maxCnt = 0;

    public int[] FindFrequentTreeSum(TreeNode root) {
        DFS(root);
        IList<int> ans = new List<int>();
        foreach (KeyValuePair<int, int> pair in cnt) {
            int s = pair.Key, c = pair.Value;
            if (c == maxCnt) {
                ans.Add(s);
            }
        }
        return ans.ToArray();
    }

    public int DFS(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int sum = node.val + DFS(node.left) + DFS(node.right);
        if (!cnt.ContainsKey(sum)) {
            cnt.Add(sum, 0);
        }
        maxCnt = Math.Max(maxCnt, ++cnt[sum]);
        return sum;
    }
}

[sol1-Golang]

func findFrequentTreeSum(root *TreeNode) (ans []int) {
    cnt := map[int]int{}
    maxCnt := 0
    var dfs func(*TreeNode) int
    dfs = func(node *TreeNode) int {
        if node == nil {
            return 0
        }
        sum := node.Val + dfs(node.Left) + dfs(node.Right)
        cnt[sum]++
        if cnt[sum] > maxCnt {
            maxCnt = cnt[sum]
        }
        return sum
    }
    dfs(root)

    for s, c := range cnt {
        if c == maxCnt {
            ans = append(ans, s)
        }
    }
    return
}

[sol1-JavaScript]

var findFrequentTreeSum = function(root) {
    const cnt = new Map();
    let maxCnt = 0;

    const dfs = (node) => {
        if (!node) {
            return 0;
        }
        const sum = node.val + dfs(node.left) + dfs(node.right);
        cnt.set(sum, (cnt.get(sum) || 0) + 1);
        maxCnt = Math.max(maxCnt, cnt.get(sum));
        return sum;
    }

    dfs(root);
    const list = [];
    for (const [s, c] of cnt.entries()) {
        if (c === maxCnt) {
            list.push(s);
        }
    }
    const ans = new Array(list.length);
    for (let i = 0; i < list.length; ++i) {
        ans[i] = list[i];
    }
    return ans;
};

[sol1-C]

#define MAX(a, b) ((a) > (b) ? (a) : (b))

typedef struct {
    int key;
    int val;
    UT_hash_handle hh;
} HashItem;

int dfs(struct TreeNode *node, HashItem **cnt, int *maxCnt) {
    if (node == NULL) {
        return 0;
    }
    int sum = node->val + dfs(node->left, cnt, maxCnt) + dfs(node->right, cnt, maxCnt);
    HashItem *pEntry = NULL;
    HASH_FIND_INT(*cnt, &sum, pEntry);
    if (NULL == pEntry) {
        pEntry = (HashItem *)malloc(sizeof(HashItem));
        pEntry->key = sum;
        pEntry->val = 1;
        HASH_ADD_INT(*cnt, key, pEntry);
    } else {
        pEntry->val++;
    }
    *maxCnt = MAX(*maxCnt, pEntry->val);
    return sum;
}

int* findFrequentTreeSum(struct TreeNode* root, int* returnSize) {
    HashItem * cnt = NULL;
    int maxCnt = 0;
    dfs(root, &cnt, &maxCnt);
    unsigned int n = HASH_COUNT(cnt);
    int *ans = (int *)malloc(sizeof(int) * n);
    int pos = 0;
    for (HashItem *pEntry = cnt; pEntry; pEntry = pEntry->hh.next) {
        if (pEntry->val == maxCnt) {
            ans[pos++] = pEntry->key;
        }
    }
    HashItem *curr, *tmp;
    HASH_ITER(hh, cnt, curr, tmp) {
        HASH_DEL(cnt, curr);  
        free(curr);
    }
    *returnSize = pos;
    return ans;
}

复杂度分析

• 时间复杂度：O(n)，其中 n 是二叉树的结点个数。深度优先搜索的时间为 O(n)。

• 空间复杂度：O(n)。哈希表和递归的栈空间均为 O(n)。