给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node
的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意: 本题和 1038: <https://leetcode-cn.com/problems/binary-search-tree-to-
greater-sum-tree/> 相同
示例 1:
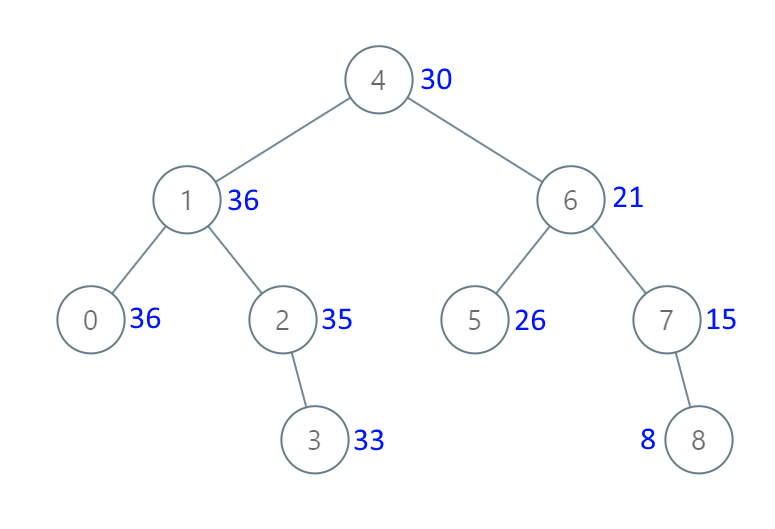
**输入:** [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
**输出:** [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
**输入:** root = [0,null,1]
**输出:** [1,null,1]
示例 3:
**输入:** root = [1,0,2]
**输出:** [3,3,2]
示例 4:
**输入:** root = [3,2,4,1]
**输出:** [7,9,4,10]
提示:
- 树中的节点数介于
0 和 104 之间。
- 每个节点的值介于
-104 和 104 之间。
- 树中的所有值 互不相同 。
- 给定的树为二叉搜索树。
前言
二叉搜索树是一棵空树,或者是具有下列性质的二叉树:
若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
它的左、右子树也分别为二叉搜索树。
由这样的性质我们可以发现,二叉搜索树的中序遍历是一个单调递增的有序序列。如果我们反序地中序遍历该二叉搜索树,即可得到一个单调递减的有序序列。
方法一:反序中序遍历
思路及算法
本题中要求我们将每个节点的值修改为原来的节点值加上所有大于它的节点值之和。这样我们只需要反序中序遍历该二叉搜索树,记录过程中的节点值之和,并不断更新当前遍历到的节点的节点值,即可得到题目要求的累加树。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution {
public:
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if (root != nullptr) {
convertBST(root->right);
sum += root->val;
root->val = sum;
convertBST(root->left);
}
return root;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
int sum = 0;
public TreeNode convertBST(TreeNode root) {
if (root != null) {
convertBST(root.right);
sum += root.val;
root.val = sum;
convertBST(root.left);
}
return root;
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
def dfs(root: TreeNode):
nonlocal total
if root:
dfs(root.right)
total += root.val
root.val = total
dfs(root.left)
total = 0
dfs(root)
return root
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| func convertBST(root *TreeNode) *TreeNode {
sum := 0
var dfs func(*TreeNode)
dfs = func(node *TreeNode) {
if node != nil {
dfs(node.Right)
sum += node.Val
node.Val = sum
dfs(node.Left)
}
}
dfs(root)
return root
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int sum;
struct TreeNode* dfs(struct TreeNode* root) {
if (root != NULL) {
dfs(root->right);
sum += root->val;
root->val = sum;
dfs(root->left);
}
return root;
}
struct TreeNode* convertBST(struct TreeNode* root) {
sum = 0;
dfs(root);
return root;
}
|
复杂度分析
方法二:Morris 遍历
思路及算法
有一种巧妙的方法可以在线性时间内,只占用常数空间来实现中序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心思想是利用树的大量空闲指针,实现空间开销的极限缩减。其反序中序遍历规则总结如下:
如果当前节点的右子节点为空,处理当前节点,并遍历当前节点的左子节点;
如果当前节点的右子节点不为空,找到当前节点右子树的最左节点(该节点为当前节点中序遍历的前驱节点);
重复步骤 1 和步骤 2,直到遍历结束。
这样我们利用 Morris 遍历的方法,反序中序遍历该二叉搜索树,即可实现线性时间与常数空间的遍历。
代码
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public:
TreeNode* getSuccessor(TreeNode* node) {
TreeNode* succ = node->right;
while (succ->left != nullptr && succ->left != node) {
succ = succ->left;
}
return succ;
}
TreeNode* convertBST(TreeNode* root) {
int sum = 0;
TreeNode* node = root;
while (node != nullptr) {
if (node->right == nullptr) {
sum += node->val;
node->val = sum;
node = node->left;
} else {
TreeNode* succ = getSuccessor(node);
if (succ->left == nullptr) {
succ->left = node;
node = node->right;
} else {
succ->left = nullptr;
sum += node->val;
node->val = sum;
node = node->left;
}
}
}
return root;
}
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| class Solution {
public TreeNode convertBST(TreeNode root) {
int sum = 0;
TreeNode node = root;
while (node != null) {
if (node.right == null) {
sum += node.val;
node.val = sum;
node = node.left;
} else {
TreeNode succ = getSuccessor(node);
if (succ.left == null) {
succ.left = node;
node = node.right;
} else {
succ.left = null;
sum += node.val;
node.val = sum;
node = node.left;
}
}
}
return root;
}
public TreeNode getSuccessor(TreeNode node) {
TreeNode succ = node.right;
while (succ.left != null && succ.left != node) {
succ = succ.left;
}
return succ;
}
}
|
[sol2-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution:
def convertBST(self, root: TreeNode) -> TreeNode:
def getSuccessor(node: TreeNode) -> TreeNode:
succ = node.right
while succ.left and succ.left != node:
succ = succ.left
return succ
total = 0
node = root
while node:
if not node.right:
total += node.val
node.val = total
node = node.left
else:
succ = getSuccessor(node)
if not succ.left:
succ.left = node
node = node.right
else:
succ.left = None
total += node.val
node.val = total
node = node.left
return roota
|
[sol2-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| func getSuccessor(node *TreeNode) *TreeNode {
succ := node.Right
for succ.Left != nil && succ.Left != node {
succ = succ.Left
}
return succ
}
func convertBST(root *TreeNode) *TreeNode {
sum := 0
node := root
for node != nil {
if node.Right == nil {
sum += node.Val
node.Val = sum
node = node.Left
} else {
succ := getSuccessor(node)
if succ.Left == nil {
succ.Left = node
node = node.Right
} else {
succ.Left = nil
sum += node.Val
node.Val = sum
node = node.Left
}
}
}
return root
}
|
[sol2-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
| struct TreeNode* getSuccessor(struct TreeNode* node) {
struct TreeNode* succ = node->right;
while (succ->left != NULL && succ->left != node) {
succ = succ->left;
}
return succ;
}
struct TreeNode* convertBST(struct TreeNode* root) {
int sum = 0;
struct TreeNode* node = root;
while (node != NULL) {
if (node->right == NULL) {
sum += node->val;
node->val = sum;
node = node->left;
} else {
struct TreeNode* succ = getSuccessor(node);
if (succ->left == NULL) {
succ->left = node;
node = node->right;
} else {
succ->left = NULL;
sum += node->val;
node->val = sum;
node = node->left;
}
}
}
return root;
}
|
复杂度分析