0560-和为 K 的子数组

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:24 2023-09-13 16:06:24 Updated    

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 _该数组中和为 k ** ** 的连续子数组的个数 _。

子数组是数组中元素的连续非空序列。

示例 1：

**输入：** nums = [1,1,1], k = 2
**输出：** 2

示例 2：

**输入：** nums = [1,2,3], k = 3
**输出：** 2

提示：

  • 1 <= nums.length <= 2 * 104
  • -1000 <= nums[i] <= 1000
  • -107 <= k <= 107

📺 视频题解

560. 和为k的子数组.mp4

📖 文字题解

方法一：枚举

思路和算法

考虑以 i 结尾和为 k 的连续子数组个数，我们需要统计符合条件的下标 j 的个数，其中 0\leq j\leq i 且 [j..i] 这个子数组的和恰好为 k 。

我们可以枚举 [0..i] 里所有的下标 j 来判断是否符合条件，可能有读者会认为假定我们确定了子数组的开头和结尾，还需要 O(n) 的时间复杂度遍历子数组来求和，那样复杂度就将达到 O(n^3) 从而无法通过所有测试用例。但是如果我们知道 [j,i] 子数组的和，就能 O(1) 推出 [j-1,i] 的和，因此这部分的遍历求和是不需要的，我们在枚举下标 j 的时候已经能 O(1) 求出 [j,i] 的子数组之和。

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.length; ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count = 0;
        for (int start = 0; start < nums.size(); ++start) {
            int sum = 0;
            for (int end = start; end >= 0; --end) {
                sum += nums[end];
                if (sum == k) {
                    count++;
                }
            }
        }
        return count;
    }
};
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
var subarraySum = function(nums, k) {
    let count = 0;
    for (let start = 0; start < nums.length; ++start) {
        let sum = 0;
        for (let end = start; end >= 0; --end) {
            sum += nums[end];
            if (sum == k) {
                count++;
            }
        }
    }
    return count;
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
func subarraySum(nums []int, k int) int {
    count := 0
    for start := 0; start < len(nums); start++ {
        sum := 0
        for end := start; end >= 0; end-- {
            sum += nums[end]
            if sum == k {
                count++
            }
        }
    }
    return count
}

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 为数组的长度。枚举子数组开头和结尾需要 O(n^2) 的时间，其中求和需要 O(1) 的时间复杂度，因此总时间复杂度为 O(n^2)。

  • 空间复杂度：O(1)。只需要常数空间存放若干变量。

方法二：前缀和 + 哈希表优化

思路和算法

我们可以基于方法一利用数据结构进行进一步的优化，我们知道方法一的瓶颈在于对每个 i，我们需要枚举所有的 j 来判断是否符合条件，这一步是否可以优化呢？答案是可以的。

我们定义 pre}[i] 为 [0..i] 里所有数的和，则 pre}[i] 可以由 pre}[i-1] 递推而来，即：

\textit{pre}[i]=\textit{pre}[i-1]+\textit{nums}[i]

那么「[j..i] 这个子数组和为 k 」这个条件我们可以转化为

\textit{pre}[i]-\textit{pre}[j-1]==k

简单移项可得符合条件的下标 j 需要满足

\textit{pre}[j-1] == \textit{pre}[i] - k

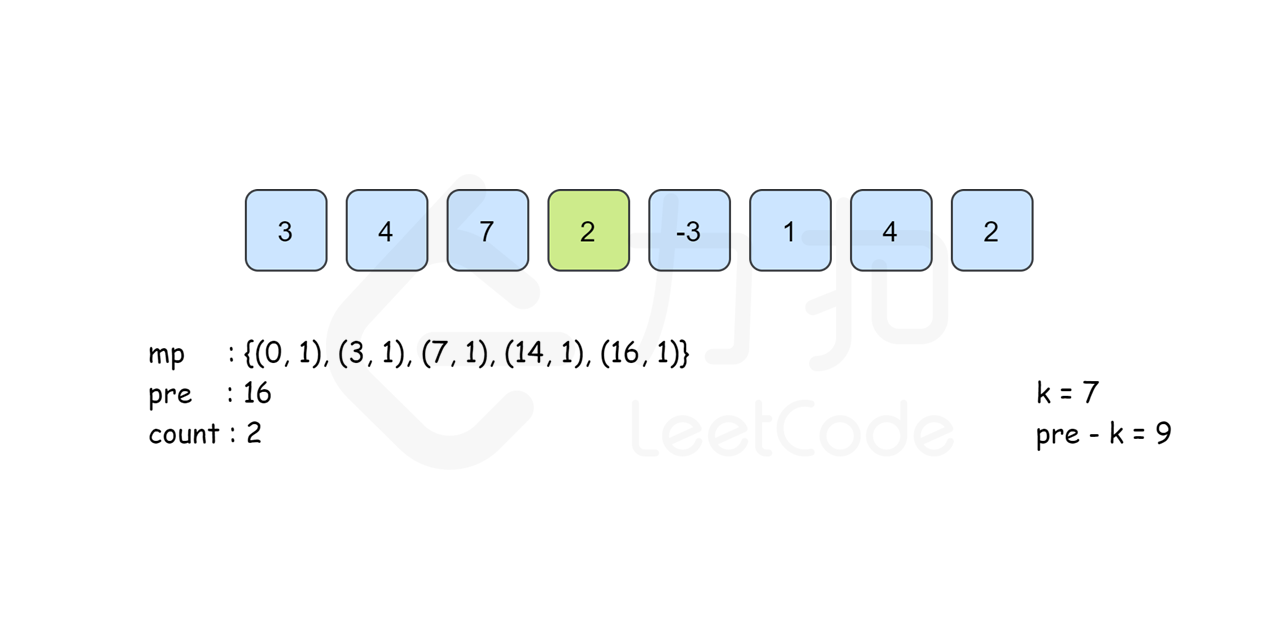
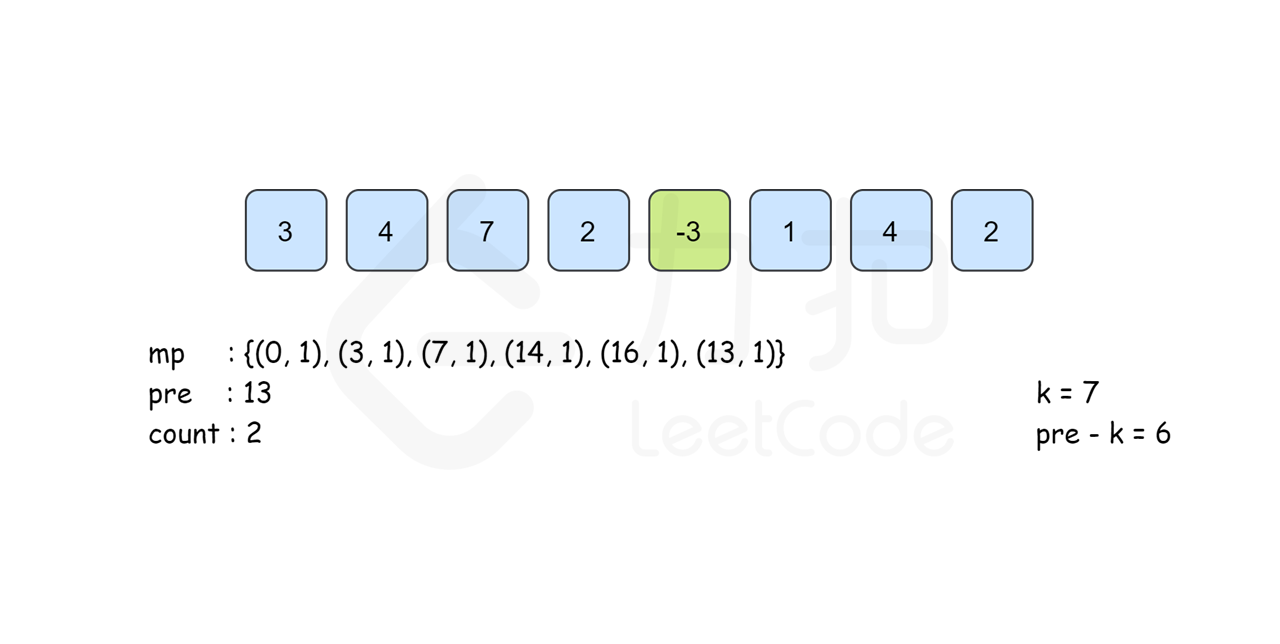
所以我们考虑以 i 结尾的和为 k 的连续子数组个数时只要统计有多少个前缀和为 pre}[i]-k 的 pre}[j] 即可。我们建立哈希表 mp，以和为键，出现次数为对应的值，记录 pre}[i] 出现的次数，从左往右边更新 mp 边计算答案，那么以 i 结尾的答案 mp}[\textit{pre}[i]-k] 即可在 O(1) 时间内得到。最后的答案即为所有下标结尾的和为 k 的子数组个数之和。

需要注意的是，从左往右边更新边计算的时候已经保证了mp}[\textit{pre}[i]-k] 里记录的 pre}[j] 的下标范围是 0\leq j\leq i 。同时，由于pre}[i] 的计算只与前一项的答案有关，因此我们可以不用建立 pre 数组，直接用 pre 变量来记录 pre[i-1] 的答案即可。

下面的动画描述了这一过程：

<fig1,fig2,fig3,fig4,fig5,fig6,fig7,fig8,fig9>

[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
    public int subarraySum(int[] nums, int k) {
        int count = 0, pre = 0;
        HashMap < Integer, Integer > mp = new HashMap < > ();
        mp.put(0, 1);
        for (int i = 0; i < nums.length; i++) {
            pre += nums[i];
            if (mp.containsKey(pre - k)) {
                count += mp.get(pre - k);
            }
            mp.put(pre, mp.getOrDefault(pre, 0) + 1);
        }
        return count;
    }
}
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        unordered_map<int, int> mp;
        mp[0] = 1;
        int count = 0, pre = 0;
        for (auto& x:nums) {
            pre += x;
            if (mp.find(pre - k) != mp.end()) {
                count += mp[pre - k];
            }
            mp[pre]++;
        }
        return count;
    }
};
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
var subarraySum = function(nums, k) {
    const mp = new Map();
    mp.set(0, 1);
    let count = 0, pre = 0;
    for (const x of nums) {
        pre += x;
        if (mp.has(pre - k)) {
            count += mp.get(pre - k);
        }
        if (mp.has(pre)) {
            mp.set(pre, mp.get(pre) + 1);
        } else {
            mp.set(pre, 1);
        }
    }
    return count;
};
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
func subarraySum(nums []int, k int) int {
    count, pre := 0, 0
    m := map[int]int{}
    m[0] = 1
    for i := 0; i < len(nums); i++ {
        pre += nums[i]
        if _, ok := m[pre - k]; ok {
            count += m[pre - k]
        }
        m[pre] += 1
    }
    return count
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为数组的长度。我们遍历数组的时间复杂度为 O(n)，中间利用哈希表查询删除的复杂度均为 O(1)，因此总时间复杂度为 O(n)。

  • 空间复杂度：O(n)，其中 n 为数组的长度。哈希表在最坏情况下可能有 n 个不同的键值，因此需要 O(n) 的空间复杂度。

 Comments
On this page
0560-和为 K 的子数组
  1. 📺 视频题解
  2. 📖 文字题解