给你一个二叉树的根节点 root ,计算并返回 整个树 的坡度 。
一个树的 节点的坡度 定义即为,该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话,左子树的节点之和为 0
;没有右子树的话也是一样。空结点的坡度是 0 。
整个树 的坡度就是其所有节点的坡度之和。
示例 1:

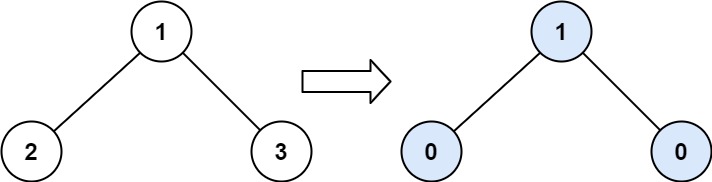
**输入:** root = [1,2,3]
**输出:** 1
**解释:**
节点 2 的坡度:|0-0| = 0(没有子节点)
节点 3 的坡度:|0-0| = 0(没有子节点)
节点 1 的坡度:|2-3| = 1(左子树就是左子节点,所以和是 2 ;右子树就是右子节点,所以和是 3 )
坡度总和:0 + 0 + 1 = 1
示例 2:

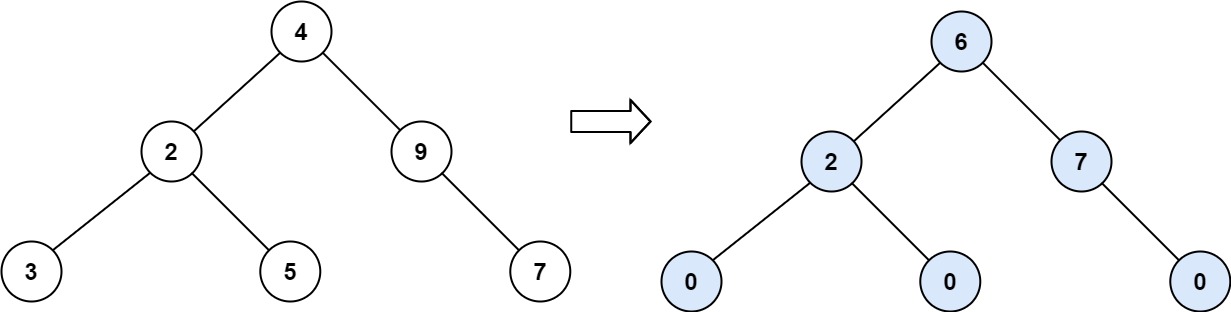
**输入:** root = [4,2,9,3,5,null,7]
**输出:** 15
**解释:**
节点 3 的坡度:|0-0| = 0(没有子节点)
节点 5 的坡度:|0-0| = 0(没有子节点)
节点 7 的坡度:|0-0| = 0(没有子节点)
节点 2 的坡度:|3-5| = 2(左子树就是左子节点,所以和是 3 ;右子树就是右子节点,所以和是 5 )
节点 9 的坡度:|0-7| = 7(没有左子树,所以和是 0 ;右子树正好是右子节点,所以和是 7 )
节点 4 的坡度:|(3+5+2)-(9+7)| = |10-16| = 6(左子树值为 3、5 和 2 ,和是 10 ;右子树值为 9 和 7 ,和是 16 )
坡度总和:0 + 0 + 0 + 2 + 7 + 6 = 15
示例 3:

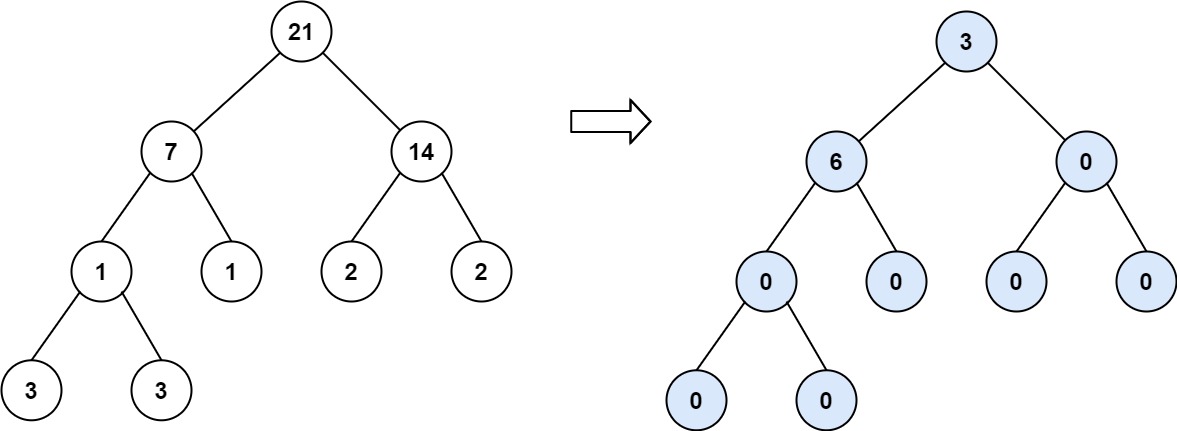
**输入:** root = [21,7,14,1,1,2,2,3,3]
**输出:** 9
提示:
- 树中节点数目的范围在
[0, 104] 内
-1000 <= Node.val <= 1000
方法一:深度优先搜索
思路和算法
根据题意,我们需要累计二叉树中所有结点的左子树结点之和与右子树结点之和的差的绝对值。因此,我们可以使用深度优先搜索,在遍历每个结点时,累加其左子树结点之和与右子树结点之和的差的绝对值,并返回以其为根结点的树的结点之和。
具体地,我们实现算法如下:
- 从根结点开始遍历,设当前遍历的结点为 node;
- 遍历 node 的左子结点,得到左子树结点之和 sum_left;遍历 node 的右子结点,得到右子树结点之和 sum_right;
- 将左子树结点之和与右子树结点之和的差的绝对值累加到结果变量 ans;
- 返回以 node 作为根结点的树的结点之和 sum_left} + \textit{sum_right} + \textit{node}.\textit{val。
代码
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution:
def __init__(self):
self.ans = 0
def findTilt(self, root: TreeNode) -> int:
self.dfs(root)
return self.ans
def dfs(self, node):
if not node:
return 0
sum_left = self.dfs(node.left)
sum_right = self.dfs(node.right)
self.ans += abs(sum_left - sum_right)
return sum_left + sum_right + node.val
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution {
int ans = 0;
public int findTilt(TreeNode root) {
dfs(root);
return ans;
}
public int dfs(TreeNode node) {
if (node == null) {
return 0;
}
int sumLeft = dfs(node.left);
int sumRight = dfs(node.right);
ans += Math.abs(sumLeft - sumRight);
return sumLeft + sumRight + node.val;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public class Solution {
int ans = 0;
public int FindTilt(TreeNode root) {
DFS(root);
return ans;
}
public int DFS(TreeNode node) {
if (node == null) {
return 0;
}
int sumLeft = DFS(node.left);
int sumRight = DFS(node.right);
ans += Math.Abs(sumLeft - sumRight);
return sumLeft + sumRight + node.val;
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| class Solution {
public:
int ans = 0;
int findTilt(TreeNode* root) {
dfs(root);
return ans;
}
int dfs(TreeNode* node) {
if (node == nullptr) {
return 0;
}
int sumLeft = dfs(node->left);
int sumRight = dfs(node->right);
ans += abs(sumLeft - sumRight);
return sumLeft + sumRight + node->val;
}
};
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| var findTilt = function(root) {
let ans = 0;
const dfs = (node) => {
if (!node) {
return 0;
}
const sumLeft = dfs(node.left);
const sumRight = dfs(node.right);
ans += Math.abs(sumLeft - sumRight);
return sumLeft + sumRight + node.val;
}
dfs(root);
return ans;
};
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| func findTilt(root *TreeNode) (ans int) {
var dfs func(*TreeNode) int
dfs = func(node *TreeNode) int {
if node == nil {
return 0
}
sumLeft := dfs(node.Left)
sumRight := dfs(node.Right)
ans += abs(sumLeft - sumRight)
return sumLeft + sumRight + node.Val
}
dfs(root)
return
}
func abs(x int) int {
if x < 0 {
return -x
}
return x
}
|
复杂度分析