给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn]最多 可以移动 maxMove 次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn109 + 7 取余 后的结果。
示例 1:
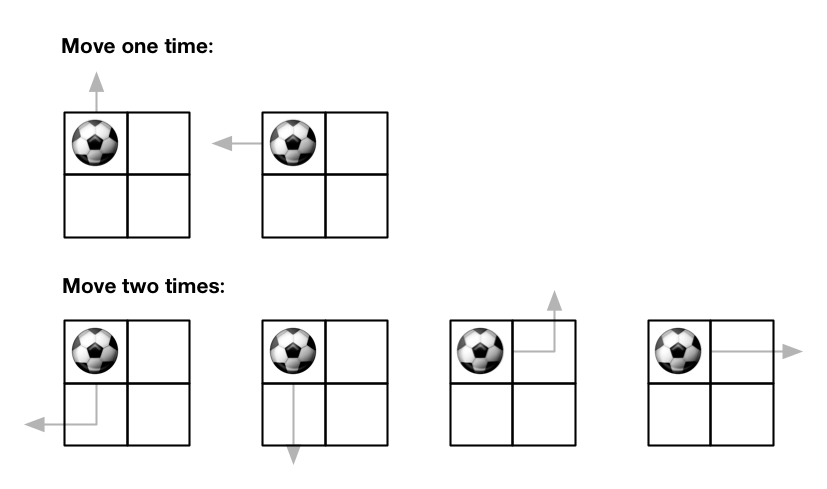
**输入:** m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
**输出:** 6
示例 2:
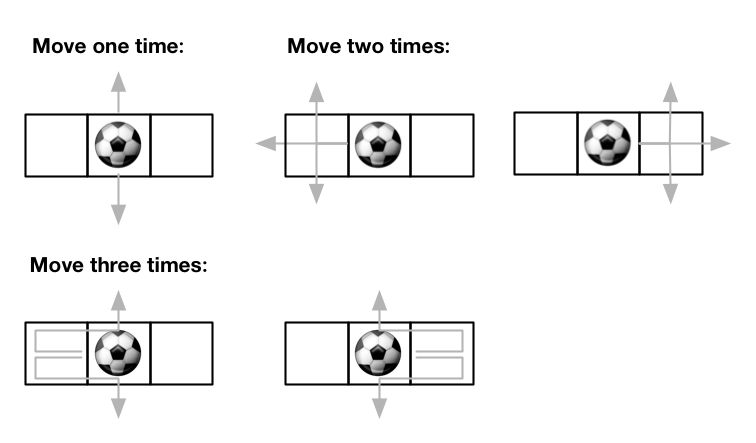
**输入:** m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
**输出:** 12
提示:
1 <= m, n <= 500 <= maxMove <= 500 <= startRow < m0 <= startColumn < n
方法一:动态规划 可以使用动态规划计算出界的路径数。
动态规划的状态由移动次数、行和列决定,定义 dp}[i][j][k] 表示球移动 i 次之后位于坐标 (j, k) 的路径数量。当 i=0 时,球一定位于起始坐标 (\textit{startRow}, \textit{startColumn}),因此动态规划的边界情况是:dp}[0][\textit{startRow}][\textit{startColumn}]=1,当 (j, k) \ne (\textit{startRow}, \textit{startColumn}) 时有 dp}[0][j][k]=0。
如果球移动了 i 次之后位于坐标 (j, k),且 i < \textit{maxMove,0 \le j < m,0 \le k < n,则移动第 i+1 次之后,球一定位于和坐标 (j, k) 相邻的一个坐标,记为 (j’, k’)。
由于最多可以移动的次数是 maxMove,因此遍历 0 \le i < \textit{maxMove,根据 dp}[i][][] 计算 dp}[i+1][][] 的值以及出界的路径数,即可得到最多移动 maxMove 次的情况下的出界的路径数。
根据上述思路,可以得到时间复杂度和空间复杂度都是 O(\textit{maxMove} \times m \times n) 的实现。
[sol11-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Solution { public int findPaths (int m, int n, int maxMove, int startRow, int startColumn) { final int MOD = 1000000007 ; int [][] directions = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; int outCounts = 0 ; int [][][] dp = new int [maxMove + 1 ][m][n]; dp[0 ][startRow][startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[i][j][k]; if (count > 0 ) { for (int [] direction : directions) { int j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dp[i + 1 ][j1][k1] = (dp[i + 1 ][j1][k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } } return outCounts; } }
[sol11-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 public class Solution { public int FindPaths (int m, int n, int maxMove, int startRow, int startColumn const int MOD = 1000000007 ; int [][] directions = new int [][] { new int []{-1 , 0 }, new int []{1 , 0 }, new int []{0 , -1 }, new int []{0 , 1 } }; int outCounts = 0 ; int [,,] dp = new int [maxMove + 1 , m, n]; dp[0 , startRow, startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[i, j, k]; if (count > 0 ) { foreach (int [] direction in directions) { int j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dp[i + 1 , j1, k1] = (dp[i + 1 , j1, k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } } return outCounts; } }
[sol11-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution : def findPaths (self, m: int , n: int , maxMove: int , startRow: int , startColumn: int ) -> int : MOD = 10 **9 + 7 outCounts = 0 dp = [[[0 ] * n for _ in range (m)] for _ in range (maxMove + 1 )] dp[0 ][startRow][startColumn] = 1 for i in range (maxMove): for j in range (m): for k in range (n): if dp[i][j][k] > 0 : for j1, k1 in [(j - 1 , k), (j + 1 , k), (j, k - 1 ), (j, k + 1 )]: if 0 <= j1 < m and 0 <= k1 < n: dp[i + 1 ][j1][k1] = (dp[i + 1 ][j1][k1] + dp[i][j][k]) % MOD else : outCounts = (outCounts + dp[i][j][k]) % MOD return outCounts
[sol11-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 const mod int = 1e9 + 7 var dirs = []struct { x, y int }{{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }} func findPaths (m, n, maxMove, startRow, startColumn int ) int ) { dp := make ([][][]int , maxMove+1 ) for i := range dp { dp[i] = make ([][]int , m) for j := range dp[i] { dp[i][j] = make ([]int , n) } } dp[0 ][startRow][startColumn] = 1 for i := 0 ; i < maxMove; i++ { for j := 0 ; j < m; j++ { for k := 0 ; k < n; k++ { count := dp[i][j][k] if count > 0 { for _, dir := range dirs { j1, k1 := j+dir.x, k+dir.y if j1 >= 0 && j1 < m && k1 >= 0 && k1 < n { dp[i+1 ][j1][k1] = (dp[i+1 ][j1][k1] + count) % mod } else { ans = (ans + count) % mod } } } } } } return }
[sol11-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution {public : static constexpr int MOD = 1'000'000'007 ; int findPaths (int m, int n, int maxMove, int startRow, int startColumn) vector<vector<int >> directions = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; int outCounts = 0 ; vector<vector<vector<int >>> dp (maxMove + 1 , vector<vector<int >>(m, vector <int >(n))); dp[0 ][startRow][startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[i][j][k]; if (count > 0 ) { for (auto &direction : directions) { int j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dp[i + 1 ][j1][k1] = (dp[i + 1 ][j1][k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } } return outCounts; } };
[sol11-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 int MOD = 1000000007 ;int findPaths (int m, int n, int maxMove, int startRow, int startColumn) { int directions[4 ][2 ] = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; int outCounts = 0 ; int dp[maxMove + 1 ][m][n]; memset (dp, 0 , sizeof (dp)); dp[0 ][startRow][startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[i][j][k]; if (count > 0 ) { for (int s = 0 ; s < 4 ; s++) { int j1 = j + directions[s][0 ], k1 = k + directions[s][1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dp[i + 1 ][j1][k1] = (dp[i + 1 ][j1][k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } } return outCounts; }
注意到 dp}[i][][] 只在计算 dp}[i+1][][] 时会用到,因此可以将 dp 中的移动次数的维度省略,将空间复杂度优化到 O(m \times n)。
[sol12-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class Solution { public int findPaths (int m, int n, int maxMove, int startRow, int startColumn) { final int MOD = 1000000007 ; int [][] directions = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; int outCounts = 0 ; int [][] dp = new int [m][n]; dp[startRow][startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { int [][] dpNew = new int [m][n]; for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[j][k]; if (count > 0 ) { for (int [] direction : directions) { int j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dpNew[j1][k1] = (dpNew[j1][k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } dp = dpNew; } return outCounts; } }
[sol12-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 public class Solution { public int FindPaths (int m, int n, int maxMove, int startRow, int startColumn const int MOD = 1000000007 ; int [][] directions = new int [][] { new int []{-1 , 0 }, new int []{1 , 0 }, new int []{0 , -1 }, new int []{0 , 1 } }; int outCounts = 0 ; int [,] dp = new int [m, n]; dp[startRow, startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { int [,] dpNew = new int [m, n]; for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[j, k]; if (count > 0 ) { foreach (int [] direction in directions) { int j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dpNew[j1, k1] = (dpNew[j1, k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } dp = dpNew; } return outCounts; } }
[sol12-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 var findPaths = function (m, n, maxMove, startRow, startColumn ) { const MOD = 1000000007 ; const directions = [[-1 , 0 ], [1 , 0 ], [0 , -1 ], [0 , 1 ]]; let outCounts = 0 ; let dp = new Array (m).fill (0 ).map (() => new Array (n).fill (0 )); dp[startRow][startColumn] = 1 ; for (let i = 0 ; i < maxMove; i++) { const dpNew = new Array (m).fill (0 ).map (() => new Array (n).fill (0 )); for (let j = 0 ; j < m; j++) { for (let k = 0 ; k < n; k++) { const count = dp[j][k]; if (count > 0 ) { for (const direction of directions) { let j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dpNew[j1][k1] = (dpNew[j1][k1] + count) % MOD ; } else { outCounts = (outCounts + count) % MOD ; } } } } } dp = dpNew; } return outCounts; };
[sol12-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 class Solution : def findPaths (self, m: int , n: int , maxMove: int , startRow: int , startColumn: int ) -> int : MOD = 10 **9 + 7 outCounts = 0 dp = [[0 ] * n for _ in range (m)] dp[startRow][startColumn] = 1 for i in range (maxMove): dpNew = [[0 ] * n for _ in range (m)] for j in range (m): for k in range (n): if dp[j][k] > 0 : for j1, k1 in [(j - 1 , k), (j + 1 , k), (j, k - 1 ), (j, k + 1 )]: if 0 <= j1 < m and 0 <= k1 < n: dpNew[j1][k1] = (dpNew[j1][k1] + dp[j][k]) % MOD else : outCounts = (outCounts + dp[j][k]) % MOD dp = dpNew return outCounts
[sol12-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 const mod int = 1e9 + 7 var dirs = []struct { x, y int }{{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }} func findPaths (m, n, maxMove, startRow, startColumn int ) int ) { dp := make ([][]int , m) for i := range dp { dp[i] = make ([]int , n) } dp[startRow][startColumn] = 1 for i := 0 ; i < maxMove; i++ { dpNew := make ([][]int , m) for j := range dpNew { dpNew[j] = make ([]int , n) } for j := 0 ; j < m; j++ { for k := 0 ; k < n; k++ { count := dp[j][k] if count > 0 { for _, dir := range dirs { j1, k1 := j+dir.x, k+dir.y if j1 >= 0 && j1 < m && k1 >= 0 && k1 < n { dpNew[j1][k1] = (dpNew[j1][k1] + count) % mod } else { ans = (ans + count) % mod } } } } } dp = dpNew } return }
[sol12-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 class Solution {public : static constexpr int MOD = 1'000'000'007 ; int findPaths (int m, int n, int maxMove, int startRow, int startColumn) vector<vector<int >> directions = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; int outCounts = 0 ; vector<vector<int >> dp (m, vector <int >(n)); dp[startRow][startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { vector<vector<int >> dpNew (m, vector <int >(n)); for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[j][k]; if (count > 0 ) { for (auto & direction : directions) { int j1 = j + direction[0 ], k1 = k + direction[1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dpNew[j1][k1] = (dpNew[j1][k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } dp = dpNew; } return outCounts; } };
[sol12-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 int MOD = 1000000007 ;int findPaths (int m, int n, int maxMove, int startRow, int startColumn) { int directions[4 ][2 ] = {{-1 , 0 }, {1 , 0 }, {0 , -1 }, {0 , 1 }}; int outCounts = 0 ; int dp[m][n]; memset (dp, 0 , sizeof (dp)); dp[startRow][startColumn] = 1 ; for (int i = 0 ; i < maxMove; i++) { int dpNew[m][n]; memset (dpNew, 0 , sizeof (dpNew)); for (int j = 0 ; j < m; j++) { for (int k = 0 ; k < n; k++) { int count = dp[j][k]; if (count > 0 ) { for (int s = 0 ; s < 4 ; s++) { int j1 = j + directions[s][0 ], k1 = k + directions[s][1 ]; if (j1 >= 0 && j1 < m && k1 >= 0 && k1 < n) { dpNew[j1][k1] = (dpNew[j1][k1] + count) % MOD; } else { outCounts = (outCounts + count) % MOD; } } } } } memcpy (dp, dpNew, sizeof (dp)); } return outCounts; }
复杂度分析