0598-范围求和 II

给你一个 m x n 的矩阵 M ** ** ，初始化时所有的 0 和一个操作数组 op ，其中 ops[i] = [ai, bi]
意味着当所有的 0 <= x < ai 和 0 <= y < bi 时， M[x][y] 应该加 1。

在 执行完所有操作后 ，计算并返回 矩阵中最大整数的个数 。

示例 1:

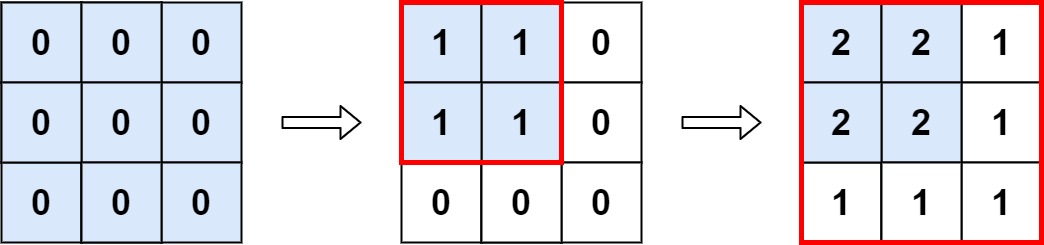
**输入:** m = 3, n = 3，ops = [[2,2],[3,3]]
**输出:** 4
**解释:** M 中最大的整数是 2, 而且 M 中有4个值为2的元素。因此返回 4。

示例 2:

**输入:** m = 3, n = 3, ops = [[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3],[2,2],[3,3],[3,3],[3,3]]
**输出:** 4

示例 3:

**输入:** m = 3, n = 3, ops = []
**输出:** 9

提示:

• 1 <= m, n <= 4 * 104
• 0 <= ops.length <= 104
• ops[i].length == 2
• 1 <= ai <= m
• 1 <= bi <= n

方法一：维护所有操作的交集

思路与算法

对于每一次操作，给定 (a, b)，我们会将矩阵中所有满足 0 \leq i < a 以及 0 \leq j < b 的位置 (i, j) 全部加上 1。由于 a, b 均为正整数，那么 (0, 0) 总是满足上述条件，并且最终位置 (0, 0) 的值就等于操作的次数。

因此，我们的任务即为找出矩阵中所有满足要求的次数恰好等于操作次数的位置。假设操作次数为 k，那么 (i, j) 需要满足：

\begin{cases}
0 \leq i < a_0, 0 \leq i < a_1, \cdots, 0 \leq i < a_{k-1} \
0 \leq j < b_0, 0 \leq j < b_1, \cdots, 0 \leq j < b_{k-1} \
\end{cases}

等价于：

\begin{cases}\tag{1}
0 \leq i < \min\limits_k a \
0 \leq j < \min\limits_k b
\end{cases}

这样一来，我们只需要求出 a 和 b 中的最小值，分别记为 \min\limits_k a 以及 \min\limits_k b，那么满足 (1) 式的 (i, j) 一共有 \min\limits_k a \times \min\limits_k b 对。

代码

[sol1-C++]

class Solution {
public:
    int maxCount(int m, int n, vector<vector<int>>& ops) {
        int mina = m, minb = n;
        for (const auto& op: ops) {
            mina = min(mina, op[0]);
            minb = min(minb, op[1]);
        }
        return mina * minb;
    }
};

[sol1-Java]

class Solution {
    public int maxCount(int m, int n, int[][] ops) {
        int mina = m, minb = n;
        for (int[] op : ops) {
            mina = Math.min(mina, op[0]);
            minb = Math.min(minb, op[1]);
        }
        return mina * minb;
    }
}

[sol1-C#]

public class Solution {
    public int MaxCount(int m, int n, int[][] ops) {
        int mina = m, minb = n;
        foreach (int[] op in ops) {
            mina = Math.Min(mina, op[0]);
            minb = Math.Min(minb, op[1]);
        }
        return mina * minb;
    }
}

[sol1-Python3]

class Solution:
    def maxCount(self, m: int, n: int, ops: List[List[int]]) -> int:
        mina, minb = m, n
        for a, b in ops:
            mina = min(mina, a)
            minb = min(minb, b)
        return mina * minb

[sol1-JavaScript]

var maxCount = function(m, n, ops) {
    let mina = m, minb = n;
    for (const op of ops) {
        mina = Math.min(mina, op[0]);
        minb = Math.min(minb, op[1]);
    }
    return mina * minb;
};

[sol1-Golang]

func maxCount(m, n int, ops [][]int) int {
    mina, minb := m, n
    for _, op := range ops {
        mina = min(mina, op[0])
        minb = min(minb, op[1])
    }
    return mina * minb
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

复杂度分析

• 时间复杂度：O(k)，其中 k 是数组 ops 的长度。

• 空间复杂度：O(1)。