0600-不含连续1的非负整数

给定一个正整数 n ，请你统计在 [0, n] 范围的非负整数中，有多少个整数的二进制表示中不存在 连续的 1 。

示例 1:

**输入:** n = 5
**输出:** 5
**解释:** 
下面列出范围在 [0, 5] 的非负整数与其对应的二进制表示：
0 : 0
1 : 1
2 : 10
3 : 11
4 : 100
5 : 101
其中，只有整数 3 违反规则（有两个连续的 1 ），其他 5 个满足规则。

示例 2:

**输入:** n = 1
**输出:** 2

示例 3:

**输入:** n = 2
**输出:** 3

提示:

• 1 <= n <= 109

方法一：动态规划

思路

因为正整数 n 可以取到 10^9，所以显然是不可能通过暴力遍历从 1 到 n 的所有正整数来计算答案的。直观上，我们也可以感觉到，在暴力遍历的过程中，有非常多的计算是重复的。因此，我们考虑通过优化暴力遍历来解决这个问题。

为了形象地将重复计算的部分找出来，我们不妨将小于等于 n 的非负整数用 01 字典树的形式表示，其中的每一条从根结点到叶结点的路径都是一个小于等于 n 的非负整数（包含前导 0）。

于是，题目可以转化为：在由所有小于等于 n 的非负整数构成的 01 字典树中，找出不包含连续 1 的从根结点到叶结点的路径数量。

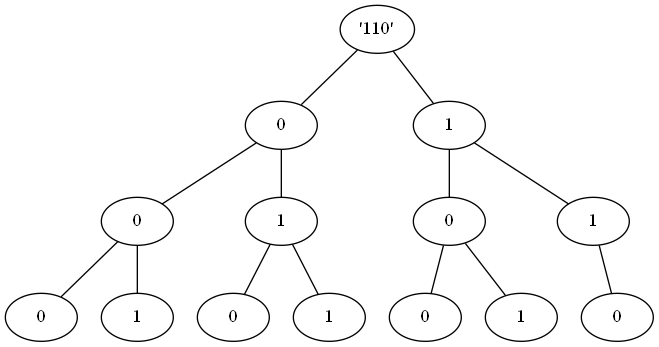
以 n = 6 = (110)_2 为例，我们可以发现：

• 对于 01 字典树中的两个节点 n_1 和 n_2，如果它们的高度相同，节点的值也相同，并且以它们为根结点的两棵子树都是满二叉树，那么它们包含的无连续 1 的从根结点到叶结点的路径个数是相同的。
• 对于 01 字典树中的两个结点 n_1 和 n_2，如果 n_2 是 n_1 的子结点，并且它们的值都是 1，那么所有经过 n_1 和 n_2 的从根结点到叶结点的路径都一定包含连续的 1。

注意到由小于等于 n 的非负整数构成的 01 字典树是完全二叉树。于是有：如果某个结点包含两个子结点，那么其左子结点为根结点是 0 的满二叉树，其右子结点为根结点是 1 的完全二叉树；如果某个结点只有一个子结点，那么其左子结点为根结点是 0 的完全二叉树。

我们在计算不包含连续 1 的从根结点到叶结点的路径数量时，可以不断地将字典树拆分为根结点为 0 的满二叉树和根结点不定的完全二叉树。

于是，题目被拆分为以下两个子问题：

• 问题 1：如何计算根结点为 0 的满二叉树中，不包含连续 1 的从根结点到叶结点的路径数量。
• 问题 2：如何将将字典树拆分为根结点为 0 的满二叉树和根结点不定的完全二叉树。

算法

首先解决第 1 个问题。

我们发现，在高度为 t、根结点为 0 的满二叉树中：其左子结点是高度为 t-1、根结点为 0 的满二叉树。其右子结点是高度为 t-1、根结点为 1 的满二叉树；但是因为路径中不能有连续 1，所以右子结点下只有其左子结点包含的从根结点到叶结点的路径才符合要求，而其左子结点是高度为 t-2、根结点为 0 的满二叉树。

于是，高度为 t、根结点为 0 的满二叉树中不包含连续 1 的从根结点到叶结点的路径数量，等于高度为 t-1、根结点为 0 的满二叉树中的路径数量与高度为 t-2，根结点为 0 的满二叉树中的路径数量之和。因此，这个问题可以通过动态规划解决：

状态：dp}[t]。dp}[t] 表示高度为 t-1、根结点为 0 的满二叉树中，不包含连续 1 的从根结点到叶结点的路径数量。

状态转移方程：

dp[t] =
\begin{cases}
dp[t-1] + dp[t-2], \quad t \ge 2 \
1, \quad t < 2
\end{cases}

接着解决第 2 个问题。

考虑到 01 字典树作为完全二叉树所具有的性质，我们可以从根结点开始处理。如果当前结点包含两个子结点，则用问题 1 的解决方法计算其左子结点中不包含连续 1 的从根结点到叶结点的路径数量，并继续处理其右子结点；如果当前结点只包含一个左子结点，那么继续处理其左子结点。

在实现中，需要注意如果已经出现连续 1 则不用继续处理；另外，叶结点没有子结点，需要作为特殊情况单独处理。

代码

[sol1-Python3]

class Solution:
    def findIntegers(self, n: int) -> int:
        dp = [0] * 31
        dp[0] = 1
        dp[1] = 1
        for i in range(2, 31):
            dp[i] = dp[i - 1] + dp[i - 2]

        pre = 0
        res = 0

        for i in range(29, -1, -1):
            val = (1 << i)
            if n & val:
                res += dp[i + 1]
                if pre == 1:
                    break
                pre = 1
            else:
                pre = 0

            if i == 0:
                res += 1

        return res

[sol1-Java]

class Solution {
    public int findIntegers(int n) {
        int[] dp = new int[31];
        dp[0] = dp[1] = 1;
        for (int i = 2; i < 31; ++i) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        int pre = 0, res = 0;
        for (int i = 29; i >= 0; --i) {
            int val = 1 << i;
            if ((n & val) != 0) {
                res += dp[i + 1];
                if (pre == 1) {
                    break;
                }
                pre = 1;
            } else {
                pre = 0;
            }

            if (i == 0) {
                ++res;
            }
        }

        return res;
    }
}

[sol1-C#]

public class Solution {
    public int FindIntegers(int n) {
        int[] dp = new int[31];
        dp[0] = dp[1] = 1;
        for (int i = 2; i < 31; ++i) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        int pre = 0, res = 0;
        for (int i = 29; i >= 0; --i) {
            int val = 1 << i;
            if ((n & val) != 0) {
                res += dp[i + 1];
                if (pre == 1) {
                    break;
                }
                pre = 1;
            } else {
                pre = 0;
            }

            if (i == 0) {
                ++res;
            }
        }

        return res;
    }
}

[sol1-C++]

class Solution {
public:
    int findIntegers(int n) {
        vector<int> dp(31);
        dp[0] = dp[1] = 1;
        for (int i = 2; i < 31; ++i) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }

        int pre = 0, res = 0;
        for (int i = 29; i >= 0; --i) {
            int val = 1 << i;
            if ((n & val) != 0) {
                res += dp[i + 1];
                if (pre == 1) {
                    break;
                }
                pre = 1;
            } else {
                pre = 0;
            }

            if (i == 0) {
                ++res;
            }
        }

        return res;
    }
};

[sol1-JavaScript]

var findIntegers = function(n) {
    const dp = new Array(31).fill(0);
    dp[0] = dp[1] = 1;
    for (let i = 2; i < 31; ++i) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }

    let pre = 0, res = 0;
    for (let i = 29; i >= 0; --i) {
        let val = 1 << i;
        if ((n & val) !== 0) {
            res += dp[i + 1];
            if (pre === 1) {
                break;
            }
            pre = 1;
        } else {
            pre = 0;
        }

        if (i === 0) {
            ++res;
        }
    }

    return res;
};

[sol1-Golang]

func findIntegers(n int) (ans int) {
    dp := [31]int{1, 1}
    for i := 2; i < 31; i++ {
        dp[i] = dp[i-1] + dp[i-2]
    }
    for i, pre := 29, 0; i >= 0; i-- {
        val := 1 << i
        if n&val > 0 {
            ans += dp[i+1]
            if pre == 1 {
                break
            }
            pre = 1
        } else {
            pre = 0
        }
        if i == 0 {
            ans++
        }
    }
    return
}

复杂度分析

• 时间复杂度：O(\log (n_{\max}))，其中 n_{\max 表示 n 的最大值，本题中 n=10^9，\log (n_{\max}) \approx 30。我们需要 O(\log (n_{\max})) 的时间来计算根结点为 0 的满二叉树中不包含连续 1 的从根结点到叶结点的路径数量，以及 O(\log (n_{\max})) 的时间来迭代地处理每一个二进制位。

• 空间复杂度：O(\log (n_{\max}))。我们需要额外的一个数组保存根结点为 0 的满二叉树中不包含连续 1 的路径数量。