0623-在二叉树中增加一行

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

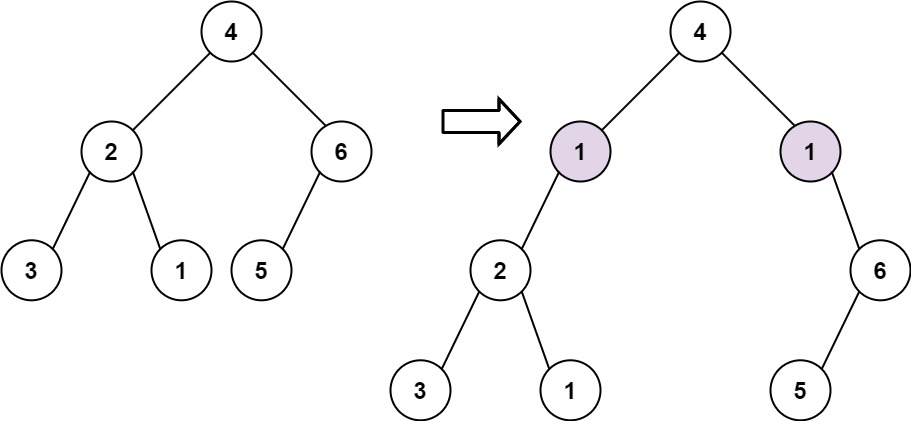
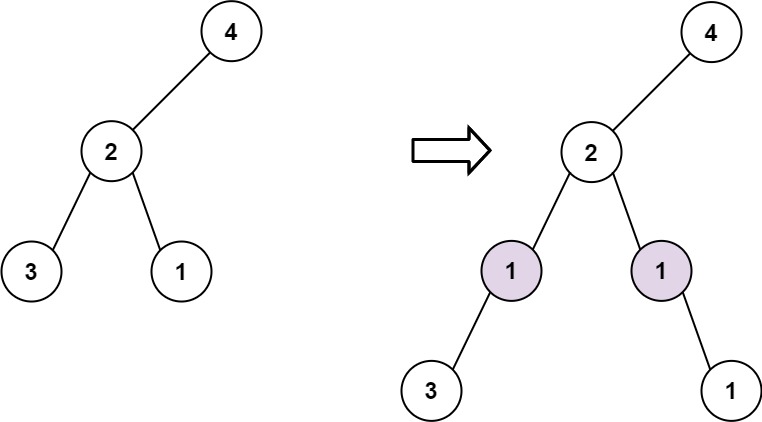
给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

  • 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
  • cur 原来的左子树应该是新的左子树根的左子树。
  • cur 原来的右子树应该是新的右子树根的右子树。
  • 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

**输入:** root = [4,2,6,3,1,5], val = 1, depth = 2
**输出:** [4,1,1,2,null,null,6,3,1,5]

示例 2:

**输入:** root = [4,2,null,3,1], val = 1, depth = 3
**输出:**  [4,2,null,1,1,3,null,null,1]

提示:

  • 节点数在 [1, 104] 范围内
  • 树的深度在 [1, 104]范围内
  • -100 <= Node.val <= 100
  • -105 <= val <= 105
  • 1 <= depth <= the depth of tree + 1

方法一：深度优先搜索

思路

当输入 depth 为 1 时，需要创建一个新的 root，并将原 root 作为新 root 的左子节点。当 depth 为 2 时，需要在 root 下新增两个节点 left 和 right 作为 root 的新子节点，并把原左子节点作为 left 的左子节点，把原右子节点作为 right 的右子节点。当 depth 大于 2 时，需要继续递归往下层搜索，并将 depth 减去 1，直到搜索到 depth 为 2。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution:
    def addOneRow(self, root: TreeNode, val: int, depth: int) -> TreeNode:
        if root == None:
            return
        if depth == 1:
            return TreeNode(val, root, None)
        if depth == 2:
            root.left = TreeNode(val, root.left, None)
            root.right = TreeNode(val, None, root.right)
        else:
            root.left = self.addOneRow(root.left, val, depth - 1)
            root.right = self.addOneRow(root.right, val, depth - 1)
        return root
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public TreeNode addOneRow(TreeNode root, int val, int depth) {
        if (root == null) {
            return null;
        }
        if (depth == 1) {
            return new TreeNode(val, root, null);
        }
        if (depth == 2) {
            root.left = new TreeNode(val, root.left, null);
            root.right = new TreeNode(val, null, root.right);
        } else {
            root.left = addOneRow(root.left, val, depth - 1);
            root.right = addOneRow(root.right, val, depth - 1);
        }
        return root;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
    public TreeNode AddOneRow(TreeNode root, int val, int depth) {
        if (root == null) {
            return null;
        }
        if (depth == 1) {
            return new TreeNode(val, root, null);
        }
        if (depth == 2) {
            root.left = new TreeNode(val, root.left, null);
            root.right = new TreeNode(val, null, root.right);
        } else {
            root.left = AddOneRow(root.left, val, depth - 1);
            root.right = AddOneRow(root.right, val, depth - 1);
        }
        return root;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if (root == nullptr) {
            return nullptr;
        }
        if (depth == 1) {
            return new TreeNode(val, root, nullptr);
        }
        if (depth == 2) {
            root->left = new TreeNode(val, root->left, nullptr);
            root->right = new TreeNode(val, nullptr, root->right);
        } else {
            root->left = addOneRow(root->left, val, depth - 1);
            root->right = addOneRow(root->right, val, depth - 1);
        }
        return root;
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
struct TreeNode* addOneRow(struct TreeNode* root, int val, int depth) {
    if (root == NULL) {
            return NULL;
        }
        struct TreeNode *node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
        if (depth == 1) {
            node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
            node->val = val;
            node->left = root;
            node->right = NULL;
            return node;
        }
        if (depth == 2) {
            node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
            node->val = val;
            node->left = root->left;
            node->right = NULL;
            root->left = node;
            node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
            node->val = val;
            node->left = NULL;
            node->right = root->right;
            root->right = node;
        } else {
            root->left = addOneRow(root->left, val, depth - 1);
            root->right = addOneRow(root->right, val, depth - 1);
        }
        return root;
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var addOneRow = function(root, val, depth) {
    if (!root) {
        return null;
    }
    if (depth === 1) {
        return new TreeNode(val, root, null);
    }
    if (depth === 2) {
        root.left = new TreeNode(val, root.left, null);
        root.right = new TreeNode(val, null, root.right);
    } else {
        root.left = addOneRow(root.left, val, depth - 1);
        root.right = addOneRow(root.right, val, depth - 1);
    }
    return root;
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
func addOneRow(root *TreeNode, val, depth int) *TreeNode {
    if root == nil {
        return nil
    }
    if depth == 1 {
        return &TreeNode{val, root, nil}
    }
    if depth == 2 {
        root.Left = &TreeNode{val, root.Left, nil}
        root.Right = &TreeNode{val, nil, root.Right}
    } else {
        root.Left = addOneRow(root.Left, val, depth-1)
        root.Right = addOneRow(root.Right, val, depth-1)
    }
    return root
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为输入的树的节点数。最坏情况下，需要遍历整棵树。

  • 空间复杂度：O(n)，递归的深度最多为 O(n)。

方法二：广度优先搜索

思路

与深度优先搜索类似，我们用广度优先搜索找到要加的一行的上一行，然后对这一行的每个节点 node，都新增两个节点 left 和 right 作为 node 的新子节点，并把原左子节点作为 left 的左子节点，把原右子节点作为 right 的右子节点。

代码

[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def addOneRow(self, root: TreeNode, val: int, depth: int) -> TreeNode:
        if depth == 1:
            return TreeNode(val, root, None)
        curLevel = [root]
        for _ in range(1, depth - 1):
            tmpt = []
            for node in curLevel:
                if node.left:
                    tmpt.append(node.left)
                if node.right:
                    tmpt.append(node.right)
            curLevel = tmpt
        for node in curLevel:
            node.left = TreeNode(val, node.left, None)
            node.right = TreeNode(val, None, node.right)
        return root
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public TreeNode addOneRow(TreeNode root, int val, int depth) {
        if (depth == 1) {
            return new TreeNode(val, root, null);
        }
        List<TreeNode> curLevel = new ArrayList<TreeNode>();
        curLevel.add(root);
        for (int i = 1; i < depth - 1; i++) {
            List<TreeNode> tmpt = new ArrayList<TreeNode>();
            for (TreeNode node : curLevel) {
                if (node.left != null) {
                    tmpt.add(node.left);
                }
                if (node.right != null) {
                    tmpt.add(node.right);
                }
            }
            curLevel = tmpt;
        }
        for (TreeNode node : curLevel) {
            node.left = new TreeNode(val, node.left, null);
            node.right = new TreeNode(val, null, node.right);
        }
        return root;
    }
}
[sol2-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class Solution {
    public TreeNode AddOneRow(TreeNode root, int val, int depth) {
        if (depth == 1) {
            return new TreeNode(val, root, null);
        }
        IList<TreeNode> curLevel = new List<TreeNode>();
        curLevel.Add(root);
        for (int i = 1; i < depth - 1; i++) {
            IList<TreeNode> tmpt = new List<TreeNode>();
            foreach (TreeNode node in curLevel) {
                if (node.left != null) {
                    tmpt.Add(node.left);
                }
                if (node.right != null) {
                    tmpt.Add(node.right);
                }
            }
            curLevel = tmpt;
        }
        foreach (TreeNode node in curLevel) {
            node.left = new TreeNode(val, node.left, null);
            node.right = new TreeNode(val, null, node.right);
        }
        return root;
    }
}
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    TreeNode* addOneRow(TreeNode* root, int val, int depth) {
        if (depth == 1) {
            return new TreeNode(val, root, nullptr);
        }
        vector<TreeNode *> curLevel(1, root);
        for (int i = 1; i < depth - 1; i++) {
            vector<TreeNode *> tmpt;
            for (auto &node : curLevel) {
                if (node->left != nullptr) {
                    tmpt.emplace_back(node->left);
                }
                if (node->right != nullptr) {
                    tmpt.emplace_back(node->right);
                }
            }
            curLevel = move(tmpt);
        }
        for (auto &node : curLevel) {
            node->left = new TreeNode(val, node->left, nullptr);
            node->right = new TreeNode(val, nullptr, node->right);
        }
        return root;
    }
};
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#define MAX_NODE_SIZE 10000

struct TreeNode* addOneRow(struct TreeNode* root, int val, int depth) {
    struct TreeNode* node = NULL;
    if (depth == 1) {
        node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
        node->val = val;
        node->left = root;
        node->right = NULL;
        return node;
    }
    struct TreeNode **queue = (struct TreeNode **)malloc(sizeof(struct TreeNode *) * MAX_NODE_SIZE);
    int head = 0, tail = 0;
    queue[tail++] = root;
    for (int i = 1; i < depth - 1; i++) {
        int sz = tail - head;
        for (int j = 0; j < sz; j++) {
            if (queue[head]->left != NULL) {
                queue[tail++] = queue[head]->left;
            }
            if (queue[head]->right != NULL) {
                queue[tail++] = queue[head]->right;
            }
            head++;
        }
    }
    for (; head != tail; head++) {
        node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
        node->val = val;
        node->left = queue[head]->left;
        node->right = NULL;
        queue[head]->left = node;
        node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
        node->val = val;
        node->left = NULL;
        node->right = queue[head]->right;
        queue[head]->right = node;
    }
    return root;
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
var addOneRow = function(root, val, depth) {
    if (depth === 1) {
        return new TreeNode(val, root, null);
    }
    let curLevel = [];
    curLevel.push(root);
    for (let i = 1; i < depth - 1; i++) {
        const tmp = [];
        for (const node of curLevel) {
            if (node.left) {
                tmp.push(node.left);
            }
            if (node.right) {
                tmp.push(node.right);
            }
        }
        curLevel = tmp;
    }
    for (const node of curLevel) {
        node.left = new TreeNode(val, node.left, null);
        node.right = new TreeNode(val, null, node.right);
    }
    return root;
};
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func addOneRow(root *TreeNode, val, depth int) *TreeNode {
    if depth == 1 {
        return &TreeNode{val, root, nil}
    }
    nodes := []*TreeNode{root}
    for i := 1; i < depth-1; i++ {
        tmp := nodes
        nodes = nil
        for _, node := range tmp {
            if node.Left != nil {
                nodes = append(nodes, node.Left)
            }
            if node.Right != nil {
                nodes = append(nodes, node.Right)
            }
        }
    }
    for _, node := range nodes {
        node.Left = &TreeNode{val, node.Left, nil}
        node.Right = &TreeNode{val, nil, node.Right}
    }
    return root
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 为输入的树的节点数。最坏情况下，需要遍历整棵树。

  • 空间复杂度：O(n)，数组空间开销最多为 O(n)。

 Comments
On this page
0623-在二叉树中增加一行