0662-二叉树最大宽度

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:24 2023-09-13 16:06:24 Updated    

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的
null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在 32 位 带符号整数范围内。

示例 1：

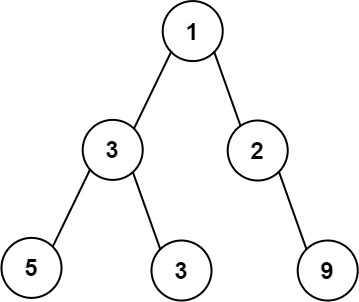
**输入：** root = [1,3,2,5,3,null,9]
**输出：** 4
**解释：** 最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

![](https://assets.leetcode.com/uploads/2022/03/14/maximum-width-of-binary-
tree-v3.jpg)

**输入：** root = [1,3,2,5,null,null,9,6,null,7]
**输出：** 7
**解释：** 最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

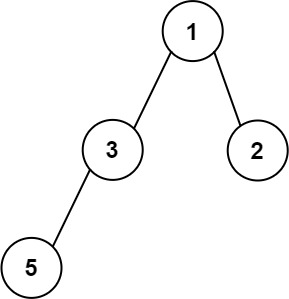
**输入：** root = [1,3,2,5]
**输出：** 2
**解释：** 最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

提示：

  • 树中节点的数目范围是 [1, 3000]
  • -100 <= Node.val <= 100

方法一：广度优先搜索

思路

此题求二叉树所有层的最大宽度，比较直观的方法是求出每一层的宽度，然后求出最大值。求每一层的宽度时，因为两端点间的 null 节点也需要计入宽度，因此可以对节点进行编号。一个编号为 index 的左子节点的编号记为 2 \times \textit{index，右子节点的编号记为 2 \times \textit{index} + 1，计算每层宽度时，用每层节点的最大编号减去最小编号再加 1 即为宽度。

遍历节点时，可以用广度优先搜索来遍历每一层的节点，并求出最大值。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution:
    def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        res = 1
        arr = [[root, 1]]
        while arr:
            tmp = []
            for node, index in arr:
                if node.left:
                    tmp.append([node.left, index * 2])
                if node.right:
                    tmp.append([node.right, index * 2 + 1])
            res = max(res, arr[-1][1] - arr[0][1] + 1)
            arr = tmp
        return res
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        int res = 1;
        List<Pair<TreeNode, Integer>> arr = new ArrayList<Pair<TreeNode, Integer>>();
        arr.add(new Pair<TreeNode, Integer>(root, 1));
        while (!arr.isEmpty()) {
            List<Pair<TreeNode, Integer>> tmp = new ArrayList<Pair<TreeNode, Integer>>();
            for (Pair<TreeNode, Integer> pair : arr) {
                TreeNode node = pair.getKey();
                int index = pair.getValue();
                if (node.left != null) {
                    tmp.add(new Pair<TreeNode, Integer>(node.left, index * 2));
                }
                if (node.right != null) {
                    tmp.add(new Pair<TreeNode, Integer>(node.right, index * 2 + 1));
                }
            }
            res = Math.max(res, arr.get(arr.size() - 1).getValue() - arr.get(0).getValue() + 1);
            arr = tmp;
        }
        return res;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class Solution {
    public int WidthOfBinaryTree(TreeNode root) {
        int res = 1;
        IList<Tuple<TreeNode, int>> arr = new List<Tuple<TreeNode, int>>();
        arr.Add(new Tuple<TreeNode, int>(root, 1));
        while (arr.Count > 0) {
            IList<Tuple<TreeNode, int>> tmp = new List<Tuple<TreeNode, int>>();
            foreach (Tuple<TreeNode, int> pair in arr) {
                TreeNode node = pair.Item1;
                int index = pair.Item2;
                if (node.left != null) {
                    tmp.Add(new Tuple<TreeNode, int>(node.left, index * 2));
                }
                if (node.right != null) {
                    tmp.Add(new Tuple<TreeNode, int>(node.right, index * 2 + 1));
                }
            }
            res = Math.Max(res, arr[arr.Count - 1].Item2 - arr[0].Item2 + 1);
            arr = tmp;
        }
        return res;
    }
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        unsigned long long res = 1;
        vector<pair<TreeNode *, unsigned long long>> arr;
        arr.emplace_back(root, 1L);
        while (!arr.empty()) {
            vector<pair<TreeNode *, unsigned long long>> tmp;
            for (auto &[node, index] : arr) {
                if (node->left) {
                    tmp.emplace_back(node->left, index * 2);
                }
                if (node->right) {
                    tmp.emplace_back(node->right, index * 2 + 1);
                }
            }
            res = max(res, arr.back().second - arr[0].second + 1);
            arr = move(tmp);
        }
        return res;
    }
};
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
#define MAX_NODE_SIZE 3000
#define MAX(a, b) ((a) > (b) ? (a) : (b))

typedef struct {
    struct TreeNode *node;
    unsigned long long index;
} Pair;

int widthOfBinaryTree(struct TreeNode* root){
    unsigned long long res = 1;
    Pair * arr = (Pair *)malloc(sizeof(Pair) * MAX_NODE_SIZE);
    Pair * tmp = (Pair *)malloc(sizeof(Pair) * MAX_NODE_SIZE);
    int arrSize = 0, tmpSize = 0;
    arr[arrSize].node = root;
    arr[arrSize].index = 1LL;
    arrSize++;
    while (arrSize > 0) {
        tmpSize = 0;
        for (int i = 0; i < arrSize; i++) {
            if (arr[i].node->left) {
                tmp[tmpSize].node = arr[i].node->left;
                tmp[tmpSize].index = arr[i].index * 2;
                tmpSize++;
            }
            if (arr[i].node->right) {
                tmp[tmpSize].node = arr[i].node->right;
                tmp[tmpSize].index = arr[i].index * 2 + 1;
                tmpSize++;
            }
        }
        res = MAX(res, arr[arrSize - 1].index - arr[0].index + 1);
        arrSize = tmpSize;
        Pair * p = arr;
        arr = tmp;
        tmp = p;
    }
    return res;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
type pair struct {
    node  *TreeNode
    index int
}

func widthOfBinaryTree(root *TreeNode) int {
    ans := 1
    q := []pair{{root, 1}}
    for q != nil {
        ans = max(ans, q[len(q)-1].index-q[0].index+1)
        tmp := q
        q = nil
        for _, p := range tmp {
            if p.node.Left != nil {
                q = append(q, pair{p.node.Left, p.index * 2})
            }
            if p.node.Right != nil {
                q = append(q, pair{p.node.Right, p.index*2 + 1})
            }
        }
    }
    return ans
}

func max(a, b int) int {
    if b > a {
        return b
    }
    return a
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点个数。需要遍历所有节点。

  • 空间复杂度：O(n)。广度优先搜索的空间复杂度最多为 O(n)。

方法二：深度优先搜索

思路

仍然按照上述方法编号，可以用深度优先搜索来遍历。遍历时如果是先访问左子节点，再访问右子节点，每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值，需要记录下来进行后续的比较。一次深度优先搜索中，需要当前节点到当前行最左边节点的宽度，以及对子节点进行深度优先搜索，求出最大宽度，并返回最大宽度。

代码

[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
class Solution:
    def widthOfBinaryTree(self, root: Optional[TreeNode]) -> int:
        levelMin = {}
        def dfs(node: Optional[TreeNode], depth: int, index: int) -> int:
            if node is None:
                return 0
            if depth not in levelMin:
                levelMin[depth] = index  # 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
            return max(index - levelMin[depth] + 1,
                       dfs(node.left, depth + 1, index * 2),
                       dfs(node.right, depth + 1, index * 2 + 1))
        return dfs(root, 1, 1)
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
    Map<Integer, Integer> levelMin = new HashMap<Integer, Integer>();

    public int widthOfBinaryTree(TreeNode root) {
        return dfs(root, 1, 1);
    }

    public int dfs(TreeNode node, int depth, int index) {
        if (node == null) {
            return 0;
        }
        levelMin.putIfAbsent(depth, index); // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
        return Math.max(index - levelMin.get(depth) + 1, Math.max(dfs(node.left, depth + 1, index * 2), dfs(node.right, depth + 1, index * 2 + 1)));
    }
}
[sol2-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
public class Solution {
    Dictionary<int, int> levelMin = new Dictionary<int, int>();

    public int WidthOfBinaryTree(TreeNode root) {
        return DFS(root, 1, 1);
    }

    public int DFS(TreeNode node, int depth, int index) {
        if (node == null) {
            return 0;
        }
        levelMin.TryAdd(depth, index); // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
        return Math.Max(index - levelMin[depth] + 1, Math.Max(DFS(node.left, depth + 1, index * 2), DFS(node.right, depth + 1, index * 2 + 1)));
    }
}
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
using ULL = unsigned long long;

class Solution {
public:
    int widthOfBinaryTree(TreeNode* root) {
        unordered_map<int, ULL> levelMin;
        function<ULL(TreeNode*, int, ULL)> dfs = [&](TreeNode* node, int depth, ULL index)->ULL {
            if (node == nullptr) {
                return 0LL;
            }
            if (!levelMin.count(depth)) {
                levelMin[depth] = index; // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
            }
            return max({index - levelMin[depth] + 1LL, dfs(node->left, depth + 1, index * 2), dfs(node->right, depth + 1, index * 2 + 1)});
        };
        return dfs(root, 1, 1LL);
    }
};
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
#define MAX(a, b) ((a) > (b) ? (a) : (b))
typedef unsigned long long ULL;

typedef struct {
    int key;
    ULL val;
    UT_hash_handle hh;
} HashItem; 

HashItem *hashFindItem(HashItem **obj, int key) {
    HashItem *pEntry = NULL;
    HASH_FIND_INT(*obj, &key, pEntry);
    return pEntry;
}

HashItem *hashAddItem(HashItem **obj, int key, ULL val) {
    HashItem *pEntry = (HashItem *)malloc(sizeof(HashItem));
    pEntry->key = key;
    pEntry->val = val;
    HASH_ADD_INT(*obj, key, pEntry);
    return pEntry;
}

bool hashSetItem(HashItem **obj, int key, ULL val) {
    HashItem *pEntry = hashFindItem(obj, key);
    if (!pEntry) {
        hashAddItem(obj, key, val);
    } else {
        pEntry->val = val;
    }
    return true;
}

ULL hashGetItem(HashItem **obj, int key, ULL defaultVal) {
    HashItem *pEntry = hashFindItem(obj, key);
    if (!pEntry) {
        return defaultVal;
    }
    return pEntry->val;
}

void hashFree(HashItem **obj) {
    HashItem *curr = NULL, *tmp = NULL;
    HASH_ITER(hh, *obj, curr, tmp) {
        HASH_DEL(*obj, curr);  
        free(curr);             
    }
}

ULL dfs(HashItem **levelMin, struct TreeNode* node, int depth, ULL index) {
    if (node == NULL) {
        return 0LL;
    }
    HashItem *pEntry = hashFindItem(levelMin, depth);
    if (!pEntry) {
        pEntry = hashAddItem(levelMin, depth, index); // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
    }
    ULL ret =  index - pEntry->val + 1;
    if (node->left) {
        ULL val = dfs(levelMin, node->left, depth + 1, index * 2);
        ret = MAX(ret, val);
    }
    if (node->right) {
        ULL val = dfs(levelMin, node->right, depth + 1, index * 2 + 1);
        ret = MAX(ret, val);
    }
    return ret;
}   

int widthOfBinaryTree(struct TreeNode* root) {
    HashItem *levelMin = NULL;
    ULL ret = dfs(&levelMin, root, 1, 1LL);
    hashFree(&levelMin);
    return ret;
}
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
func widthOfBinaryTree(root *TreeNode) int {
    levelMin := map[int]int{}
    var dfs func(*TreeNode, int, int) int
    dfs = func(node *TreeNode, depth, index int) int {
        if node == nil {
            return 0
        }
        if _, ok := levelMin[depth]; !ok {
            levelMin[depth] = index // 每一层最先访问到的节点会是最左边的节点，即每一层编号的最小值
        }
        return max(index-levelMin[depth]+1, max(dfs(node.Left, depth+1, index*2), dfs(node.Right, depth+1, index*2+1)))
    }
    return dfs(root, 1, 1)
}

func max(a, b int) int {
    if b > a {
        return b
    }
    return a
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点个数。需要遍历所有节点。

  • 空间复杂度：O(n)。递归的深度最多为 O(n)。

 Comments
On this page
0662-二叉树最大宽度