给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或
0。如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个。
更正式地说,即 root.val = min(root.left.val, root.right.val) 总成立。
给出这样的一个二叉树,你需要输出所有节点中的 第二小的值 。
如果第二小的值不存在的话,输出 -1 。
示例 1:

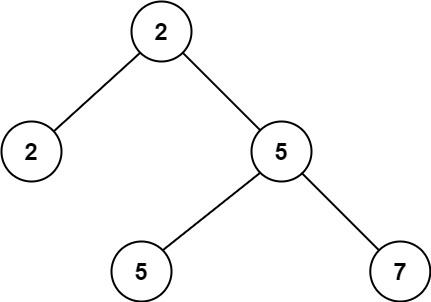
**输入:** root = [2,2,5,null,null,5,7]
**输出:** 5
**解释:** 最小的值是 2 ,第二小的值是 5 。
示例 2:

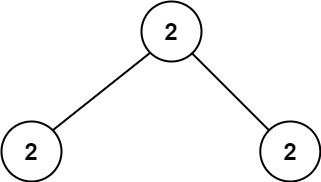
**输入:** root = [2,2,2]
**输出:** -1
**解释:** 最小的值是 2, 但是不存在第二小的值。
提示:
- 树中节点数目在范围
[1, 25] 内
1 <= Node.val <= 231 - 1- 对于树中每个节点
root.val == min(root.left.val, root.right.val)
方法一:深度优先搜索
思路
根据题目中的描述「如果一个节点有两个子节点的话,那么该节点的值等于两个子节点中较小的一个」,我们可以知道,对于二叉树中的任意节点 x,x 的值不大于其所有子节点的值,因此:
对于二叉树中的任意节点 x,x 的值不大于以 x 为根的子树中所有节点的值。
令 x 为二叉树的根节点,此时我们可以得出结论:
二叉树根节点的值即为所有节点中的最小值。
因此,我们可以对整棵二叉树进行一次遍历。设根节点的值为 rootvalue,我们只需要通过遍历,找出严格大于 rootvalue 的最小值,即为「所有节点中的第二小的值」。
算法
我们可以使用深度优先搜索的方法对二叉树进行遍历。
假设当前遍历到的节点为 node,如果 node 的值严格大于 rootvalue,那么我们就可以用 node 的值来更新答案 ans。
当我们遍历完整棵二叉树后,即可返回 ans。
细节
根据题目要求,如果第二小的值不存在的话,输出 -1,那么我们可以将 ans 的初始值置为 -1。在遍历的过程中,如果当前节点的值严格大于 rootvalue 的节点时,那么只要 ans 的值为 -1 或者当前节点的值严格小于 ans,我们就需要对 ans 进行更新。
此外,如果当前节点的值大于等于 ans,那么根据「思路」部分,以当前节点为根的子树中所有节点的值都大于等于 ans,我们就直接回溯,无需对该子树进行遍历。这样做可以省去不必要的遍历过程。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
int findSecondMinimumValue(TreeNode* root) {
int ans = -1;
int rootvalue = root->val;
function<void(TreeNode*)> dfs = [&](TreeNode* node) {
if (!node) {
return;
}
if (ans != -1 && node->val >= ans) {
return;
}
if (node->val > rootvalue) {
ans = node->val;
}
dfs(node->left);
dfs(node->right);
};
dfs(root);
return ans;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| class Solution {
int ans;
int rootvalue;
public int findSecondMinimumValue(TreeNode root) {
ans = -1;
rootvalue = root.val;
dfs(root);
return ans;
}
public void dfs(TreeNode node) {
if (node == null) {
return;
}
if (ans != -1 && node.val >= ans) {
return;
}
if (node.val > rootvalue) {
ans = node.val;
}
dfs(node.left);
dfs(node.right);
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public class Solution {
int ans;
int rootvalue;
public int FindSecondMinimumValue(TreeNode root) {
ans = -1;
rootvalue = root.val;
DFS(root);
return ans;
}
public void DFS(TreeNode node) {
if (node == null) {
return;
}
if (ans != -1 && node.val >= ans) {
return;
}
if (node.val > rootvalue) {
ans = node.val;
}
DFS(node.left);
DFS(node.right);
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| class Solution:
def findSecondMinimumValue(self, root: TreeNode) -> int:
ans, rootvalue = -1, root.val
def dfs(node: TreeNode) -> None:
nonlocal ans
if not node:
return
if ans != -1 and node.val >= ans:
return
if node.val > rootvalue:
ans = node.val
dfs(node.left)
dfs(node.right)
dfs(root)
return ans
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| var findSecondMinimumValue = function(root) {
let ans = -1;
const rootvalue = root.val;
const dfs = (node) => {
if (node === null) {
return;
}
if (ans !== -1 && node.val >= ans) {
return;
}
if (node.val > rootvalue) {
ans = node.val;
}
dfs(node.left);
dfs(node.right);
}
dfs(root);
return ans;
};
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| func findSecondMinimumValue(root *TreeNode) int {
ans := -1
rootVal := root.Val
var dfs func(*TreeNode)
dfs = func(node *TreeNode) {
if node == nil || ans != -1 && node.Val >= ans {
return
}
if node.Val > rootVal {
ans = node.Val
}
dfs(node.Left)
dfs(node.Right)
}
dfs(root)
return ans
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| int ans;
int rootvalue;
struct TreeNode *dfs(struct TreeNode *node) {
if (!node) {
return;
}
if (ans != -1 && node->val >= ans) {
return;
}
if (node->val > rootvalue) {
ans = node->val;
}
dfs(node->left);
dfs(node->right);
};
int findSecondMinimumValue(struct TreeNode *root) {
ans = -1;
rootvalue = root->val;
dfs(root);
return ans;
}
|
复杂度分析