0680-验证回文串 II

给你一个字符串 s，最多可以从中删除一个字符。

请你判断 s 是否能成为回文字符串：如果能，返回 true ；否则，返回 false 。

示例 1：

**输入：** s = "aba"
**输出：** true

示例 2：

**输入：** s = "abca"
**输出：** true
**解释：** 你可以删除字符 'c' 。

示例 3：

**输入：** s = "abc"
**输出：** false

提示：

1 <= s.length <= 105
s 由小写英文字母组成

📺视频题解

📖文字题解

方法一：贪心

考虑最朴素的方法：首先判断原串是否是回文串，如果是，就返回 true；如果不是，则枚举每一个位置作为被删除的位置，再判断剩下的字符串是否是回文串。这种做法的渐进时间复杂度是 O(n^2) 的，会超出时间限制。

我们换一种想法。首先考虑如果不允许删除字符，如何判断一个字符串是否是回文串。常见的做法是使用双指针。定义左右指针，初始时分别指向字符串的第一个字符和最后一个字符，每次判断左右指针指向的字符是否相同，如果不相同，则不是回文串；如果相同，则将左右指针都往中间移动一位，直到左右指针相遇，则字符串是回文串。

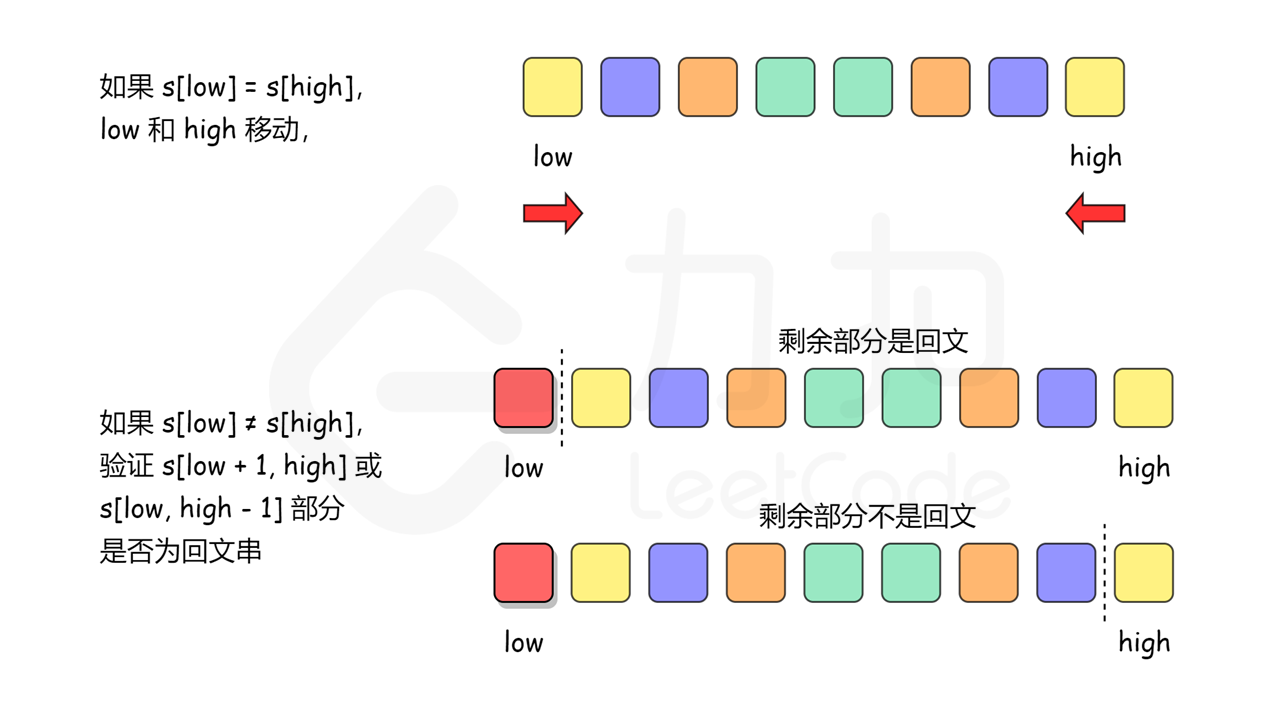
在允许最多删除一个字符的情况下，同样可以使用双指针，通过贪心实现。初始化两个指针 low 和 high 分别指向字符串的第一个字符和最后一个字符。每次判断两个指针指向的字符是否相同，如果相同，则更新指针，将 low 加 1，high 减 1，然后判断更新后的指针范围内的子串是否是回文字符串。如果两个指针指向的字符不同，则两个字符中必须有一个被删除，此时我们就分成两种情况：即删除左指针对应的字符，留下子串 s[\textit{low} + 1 : \textit{high}]，或者删除右指针对应的字符，留下子串 s[\textit{low} : \textit{high} - 1]。当这两个子串中至少有一个是回文串时，就说明原始字符串删除一个字符之后就以成为回文串。

[sol1-Java]class Solution {
    public boolean validPalindrome(String s) {
        int low = 0, high = s.length() - 1;
        while (low < high) {
            char c1 = s.charAt(low), c2 = s.charAt(high);
            if (c1 == c2) {
                ++low;
                --high;
            } else {
                return validPalindrome(s, low, high - 1) || validPalindrome(s, low + 1, high);
            }
        }
        return true;
    }

    public boolean validPalindrome(String s, int low, int high) {
        for (int i = low, j = high; i < j; ++i, --j) {
            char c1 = s.charAt(i), c2 = s.charAt(j);
            if (c1 != c2) {
                return false;
            }
        }
        return true;
    }
}

[sol1-Python3]class Solution:
    def validPalindrome(self, s: str) -> bool:
        def checkPalindrome(low, high):
            i, j = low, high
            while i < j:
                if s[i] != s[j]:
                    return False
                i += 1
                j -= 1
            return True

        low, high = 0, len(s) - 1
        while low < high:
            if s[low] == s[high]: 
                low += 1
                high -= 1
            else:
                return checkPalindrome(low + 1, high) or checkPalindrome(low, high - 1)
        return True

[sol1-C++]class Solution {
public:
    bool checkPalindrome(const string& s, int low, int high) {
        for (int i = low, j = high; i < j; ++i, --j) {
            if (s[i] != s[j]) {
                return false;
            }
        }
        return true;
    }

    bool validPalindrome(string s) {
        int low = 0, high = s.size() - 1;
        while (low < high) {
            char c1 = s[low], c2 = s[high];
            if (c1 == c2) {
                ++low;
                --high;
            } else {
                return checkPalindrome(s, low, high - 1) || checkPalindrome(s, low + 1, high);
            }
        }
        return true;
    }
};

[sol1-Golang]func validPalindrome(s string) bool {
    low, high := 0, len(s) - 1
    for low < high {
        if s[low] == s[high] {
            low++
            high--
        } else {
            flag1, flag2 := true, true
            for i, j := low, high - 1; i < j; i, j = i + 1, j - 1 {
                if s[i] != s[j] {
                    flag1 = false
                    break
                }
            }
            for i, j := low + 1, high; i < j; i, j = i + 1, j - 1 {
                if s[i] != s[j] {
                    flag2 = false
                    break
                }
            }
            return flag1 || flag2
        }
    }
    return true
}

复杂度分析

时间复杂度：O(n)，其中 n 是字符串的长度。判断整个字符串是否是回文字符串的时间复杂度是 O(n)，遇到不同字符时，判断两个子串是否是回文字符串的时间复杂度也都是 O(n)。
空间复杂度：O(1)。只需要维护有限的常量空间。