0684-冗余连接

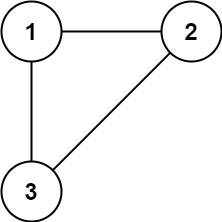
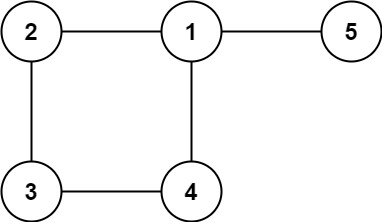
树可以看成是一个连通且 **无环 **的 **无向 **图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n
中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在
ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

**输入:** edges = [[1,2], [1,3], [2,3]]
**输出:** [2,3]

示例 2：

**输入:** edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
**输出:** [1,4]

提示:

n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的

方法一：并查集

在一棵树中，边的数量比节点的数量少 1。如果一棵树有 n 个节点，则这棵树有 n-1 条边。这道题中的图在树的基础上多了一条附加的边，因此边的数量也是 n。

树是一个连通且无环的无向图，在树中多了一条附加的边之后就会出现环，因此附加的边即为导致环出现的边。

可以通过并查集寻找附加的边。初始时，每个节点都属于不同的连通分量。遍历每一条边，判断这条边连接的两个顶点是否属于相同的连通分量。

如果两个顶点属于不同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间不连通，因此当前的边不会导致环出现，合并这两个顶点的连通分量。
如果两个顶点属于相同的连通分量，则说明在遍历到当前的边之前，这两个顶点之间已经连通，因此当前的边导致环出现，为附加的边，将当前的边作为答案返回。

[sol1-Java]class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int n = edges.length;
        int[] parent = new int[n + 1];
        for (int i = 1; i <= n; i++) {
            parent[i] = i;
        }
        for (int i = 0; i < n; i++) {
            int[] edge = edges[i];
            int node1 = edge[0], node2 = edge[1];
            if (find(parent, node1) != find(parent, node2)) {
                union(parent, node1, node2);
            } else {
                return edge;
            }
        }
        return new int[0];
    }

    public void union(int[] parent, int index1, int index2) {
        parent[find(parent, index1)] = find(parent, index2);
    }

    public int find(int[] parent, int index) {
        if (parent[index] != index) {
            parent[index] = find(parent, parent[index]);
        }
        return parent[index];
    }
}

[sol1-C++]class Solution {
public:
    int Find(vector<int>& parent, int index) {
        if (parent[index] != index) {
            parent[index] = Find(parent, parent[index]);
        }
        return parent[index];
    }

    void Union(vector<int>& parent, int index1, int index2) {
        parent[Find(parent, index1)] = Find(parent, index2);
    }

    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        vector<int> parent(n + 1);
        for (int i = 1; i <= n; ++i) {
            parent[i] = i;
        }
        for (auto& edge: edges) {
            int node1 = edge[0], node2 = edge[1];
            if (Find(parent, node1) != Find(parent, node2)) {
                Union(parent, node1, node2);
            } else {
                return edge;
            }
        }
        return vector<int>{};
    }
};

[sol1-JavaScript]var findRedundantConnection = function(edges) {
    const n = edges.length;
    const parent = new Array(n + 1).fill(0).map((value, index) => index);
    for (let i = 0; i < n; i++) {
        const edge = edges[i];
        const node1 = edge[0], node2 = edge[1];
        if (find(parent, node1) != find(parent, node2)) {
            union(parent, node1, node2);
        } else {
            return edge;
        }
    }
    return [0];
};

const union = (parent, index1, index2) => {
    parent[find(parent, index1)] = find(parent, index2);
}

const find = (parent, index) => {
    if (parent[index] !== index) {
        parent[index] = find(parent, parent[index]);
    }
    return parent[index];
}

[sol1-Python3]class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        parent = list(range(n + 1))

        def find(index: int) -> int:
            if parent[index] != index:
                parent[index] = find(parent[index])
            return parent[index]
        
        def union(index1: int, index2: int):
            parent[find(index1)] = find(index2)

        for node1, node2 in edges:
            if find(node1) != find(node2):
                union(node1, node2)
            else:
                return [node1, node2]
        
        return []

[sol1-Golang]func findRedundantConnection(edges [][]int) []int {
    parent := make([]int, len(edges)+1)
    for i := range parent {
        parent[i] = i
    }
    var find func(int) int
    find = func(x int) int {
        if parent[x] != x {
            parent[x] = find(parent[x])
        }
        return parent[x]
    }
    union := func(from, to int) bool {
        x, y := find(from), find(to)
        if x == y {
            return false
        }
        parent[x] = y
        return true
    }
    for _, e := range edges {
        if !union(e[0], e[1]) {
            return e
        }
    }
    return nil
}

[sol1-C]int Find(int* parent, int index) {
    if (parent[index] != index) {
        parent[index] = Find(parent, parent[index]);
    }
    return parent[index];
}

void Union(int* parent, int index1, int index2) {
    parent[Find(parent, index1)] = Find(parent, index2);
}

int* findRedundantConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize) {
    int n = edgesSize;
    int parent[n + 1];
    for (int i = 1; i <= n; ++i) {
        parent[i] = i;
    }
    for (int i = 0; i < edgesSize; ++i) {
        int node1 = edges[i][0], node2 = edges[i][1];
        if (Find(parent, node1) != Find(parent, node2)) {
            Union(parent, node1, node2);
        } else {
            *returnSize = 2;
            return edges[i];
        }
    }
    *returnSize = 0;
    return NULL;
}

复杂度分析

时间复杂度：O(n \log n)，其中 n 是图中的节点个数。需要遍历图中的 n 条边，对于每条边，需要对两个节点查找祖先，如果两个节点的祖先不同则需要进行合并，需要进行 2 次查找和最多 1 次合并。一共需要进行 2n 次查找和最多 n 次合并，因此总时间复杂度是 O(2n \log n)=O(n \log n)。这里的并查集使用了路径压缩，但是没有使用按秩合并，最坏情况下的时间复杂度是 O(n \log n)，平均情况下的时间复杂度依然是 O(n \alpha (n))，其中 \alpha 为阿克曼函数的反函数，\alpha (n) 可以认为是一个很小的常数。
空间复杂度：O(n)，其中 n 是图中的节点个数。使用数组 parent 记录每个节点的祖先。