0685-冗余连接 II

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

在本问题中，有根树指满足以下条件的 有向
图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。

输入一个有向图，该图由一个有着 n 个节点（节点值不重复，从 1 到 n）的树及一条附加的有向边构成。附加的边包含在 1 到 n
中的两个不同顶点间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组 edges 。 每个元素是一对 [ui, vi]，用以表示 有向 图中连接顶点 ui 和顶点 vi
的边，其中 ui 是 vi 的一个父节点。

返回一条能删除的边，使得剩下的图是有 n 个节点的有根树。若有多个答案，返回最后出现在给定二维数组的答案。

示例 1：

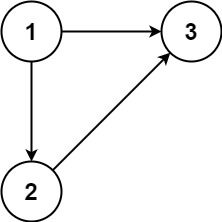
**输入：** edges = [[1,2],[1,3],[2,3]]
**输出：** [2,3]

示例 2：

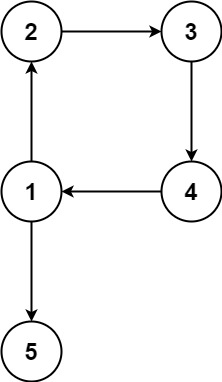
**输入：** edges = [[1,2],[2,3],[3,4],[4,1],[1,5]]
**输出：** [4,1]

提示：

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ui, vi <= n

方法一：并查集

思路与算法

在一棵树中，边的数量比节点的数量少 1。如果一棵树有 n 个节点，则这棵树有 n-1 条边。这道题中的图在树的基础上多了一条附加的边，因此边的数量也是 n。

树中的每个节点都有一个父节点，除了根节点没有父节点。在多了一条附加的边之后，可能有以下两种情况：

  • 附加的边指向根节点，则包括根节点在内的每个节点都有一个父节点，此时图中一定有环路；

  • 附加的边指向非根节点，则恰好有一个节点（即被附加的边指向的节点）有两个父节点，此时图中可能有环路也可能没有环路。

要找到附加的边，需要遍历图中的所有的边构建出一棵树，在构建树的过程中寻找导致冲突（即导致一个节点有两个父节点）的边以及导致环路出现的边。

具体做法是，使用数组 parent 记录每个节点的父节点，初始时对于任何 1 \le i \le n 都有 parent}[i]=i，另外创建并查集，初始时并查集中的每个节点都是一个连通分支，该连通分支的根节点就是该节点本身。遍历每条边的过程中，维护导致冲突的边和导致环路出现的边，由于只有一条附加的边，因此最多有一条导致冲突的边和一条导致环路出现的边。

当访问到边 [u,v] 时，进行如下操作：

  • 如果此时已经有 parent}[v] \ne v，说明 v 有两个父节点，将当前的边 [u,v] 记为导致冲突的边；

  • 否则，令 parent}[v] = u，然后在并查集中分别找到 u 和 v 的祖先（即各自的连通分支中的根节点），如果祖先相同，说明这条边导致环路出现，将当前的边 [u,v] 记为导致环路出现的边，如果祖先不同，则在并查集中将 u 和 v 进行合并。

根据上述操作，同一条边不可能同时被记为导致冲突的边和导致环路出现的边。如果访问到的边确实同时导致冲突和环路出现，则这条边被记为导致冲突的边。

在遍历图中的所有边之后，根据是否存在导致冲突的边和导致环路出现的边，得到附加的边。

如果没有导致冲突的边，说明附加的边一定导致环路出现，而且是在环路中的最后一条被访问到的边，因此附加的边即为导致环路出现的边。

如果有导致冲突的边，记这条边为 [u,v]，则有两条边指向 v，另一条边为 [\textit{parent}[v],v]，需要通过判断是否有导致环路的边决定哪条边是附加的边。

  • 如果有导致环路的边，则附加的边不可能是 [u,v]（因为 [u,v] 已经被记为导致冲突的边，不可能被记为导致环路出现的边），因此附加的边是 [\textit{parent}[v],v]。

  • 如果没有导致环路的边，则附加的边是后被访问到的指向 v 的边，因此附加的边是 [u,v]。

代码

[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    public int[] findRedundantDirectedConnection(int[][] edges) {
        int n = edges.length;
        UnionFind uf = new UnionFind(n + 1);
        int[] parent = new int[n + 1];
        for (int i = 1; i <= n; ++i) {
            parent[i] = i;
        }
        int conflict = -1;
        int cycle = -1;
        for (int i = 0; i < n; ++i) {
            int[] edge = edges[i];
            int node1 = edge[0], node2 = edge[1];
            if (parent[node2] != node2) {
                conflict = i;
            } else {
                parent[node2] = node1;
                if (uf.find(node1) == uf.find(node2)) {
                    cycle = i;
                } else {
                    uf.union(node1, node2);
                }
            }
        }
        if (conflict < 0) {
            int[] redundant = {edges[cycle][0], edges[cycle][1]};
            return redundant;
        } else {
            int[] conflictEdge = edges[conflict];
            if (cycle >= 0) {
                int[] redundant = {parent[conflictEdge[1]], conflictEdge[1]};
                return redundant;
            } else {
                int[] redundant = {conflictEdge[0], conflictEdge[1]};
                return redundant;
            }
        }
    }
}

class UnionFind {
    int[] ancestor;

    public UnionFind(int n) {
        ancestor = new int[n];
        for (int i = 0; i < n; ++i) {
            ancestor[i] = i;
        }
    }

    public void union(int index1, int index2) {
        ancestor[find(index1)] = find(index2);
    }

    public int find(int index) {
        if (ancestor[index] != index) {
            ancestor[index] = find(ancestor[index]);
        }
        return ancestor[index];
    }
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
func findRedundantDirectedConnection(edges [][]int) (redundantEdge []int) {
    n := len(edges)
    uf := newUnionFind(n + 1)
    parent := make([]int, n+1) // parent[i] 表示 i 的父节点
    for i := range parent {
        parent[i] = i
    }

    var conflictEdge, cycleEdge []int
    for _, edge := range edges {
        from, to := edge[0], edge[1]
        if parent[to] != to { // to 有两个父节点
            conflictEdge = edge
        } else {
            parent[to] = from
            if uf.find(from) == uf.find(to) { // from 和 to 已连接
                cycleEdge = edge
            } else {
                uf.union(from, to)
            }
        }
    }

    // 若不存在一个节点有两个父节点的情况，则附加的边一定导致环路出现
    if conflictEdge == nil {
        return cycleEdge
    }
    // conflictEdge[1] 有两个父节点，其中之一与其构成附加的边
    // 由于我们是按照 edges 的顺序连接的，若在访问到 conflictEdge 之前已经形成了环路，则附加的边在环上
    // 否则附加的边就是 conflictEdge
    if cycleEdge != nil {
        return []int{parent[conflictEdge[1]], conflictEdge[1]}
    }
    return conflictEdge
}

type unionFind struct {
    ancestor []int
}

func newUnionFind(n int) unionFind {
    ancestor := make([]int, n)
    for i := 0; i < n; i++ {
        ancestor[i] = i
    }
    return unionFind{ancestor}
}

func (uf unionFind) find(x int) int {
    if uf.ancestor[x] != x {
        uf.ancestor[x] = uf.find(uf.ancestor[x])
    }
    return uf.ancestor[x]
}

func (uf unionFind) union(from, to int) {
    uf.ancestor[uf.find(from)] = uf.find(to)
}
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
struct UnionFind {
    vector <int> ancestor;

    UnionFind(int n) {
        ancestor.resize(n);
        for (int i = 0; i < n; ++i) {
            ancestor[i] = i;
        }
    }

    int find(int index) {
        return index == ancestor[index] ? index : ancestor[index] = find(ancestor[index]);
    }

    void merge(int u, int v) {
        ancestor[find(u)] = find(v);
    }
};

class Solution {
public:
    vector<int> findRedundantDirectedConnection(vector<vector<int>>& edges) {
        int n = edges.size();
        UnionFind uf = UnionFind(n + 1);
        auto parent = vector<int>(n + 1);
        for (int i = 1; i <= n; ++i) {
            parent[i] = i;
        }
        int conflict = -1;
        int cycle = -1;
        for (int i = 0; i < n; ++i) {
            auto edge = edges[i];
            int node1 = edge[0], node2 = edge[1];
            if (parent[node2] != node2) {
                conflict = i;
            } else {
                parent[node2] = node1;
                if (uf.find(node1) == uf.find(node2)) {
                    cycle = i;
                } else {
                    uf.merge(node1, node2);
                }
            }
        }
        if (conflict < 0) {
            auto redundant = vector<int> {edges[cycle][0], edges[cycle][1]};
            return redundant;
        } else {
            auto conflictEdge = edges[conflict];
            if (cycle >= 0) {
                auto redundant = vector<int> {parent[conflictEdge[1]], conflictEdge[1]};
                return redundant;
            } else {
                auto redundant = vector<int> {conflictEdge[0], conflictEdge[1]};
                return redundant;
            }
        }
    }
};
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class UnionFind:
    def __init__(self, n):
        self.ancestor = list(range(n))
    
    def union(self, index1: int, index2: int):
        self.ancestor[self.find(index1)] = self.find(index2)
    
    def find(self, index: int) -> int:
        if self.ancestor[index] != index:
            self.ancestor[index] = self.find(self.ancestor[index])
        return self.ancestor[index]

class Solution:
    def findRedundantDirectedConnection(self, edges: List[List[int]]) -> List[int]:
        n = len(edges)
        uf = UnionFind(n + 1)
        parent = list(range(n + 1))
        conflict = -1
        cycle = -1
        for i, (node1, node2) in enumerate(edges):
            if parent[node2] != node2:
                conflict = i
            else:
                parent[node2] = node1
                if uf.find(node1) == uf.find(node2):
                    cycle = i
                else:
                    uf.union(node1, node2)

        if conflict < 0:
            return [edges[cycle][0], edges[cycle][1]]
        else:
            conflictEdge = edges[conflict]
            if cycle >= 0:
                return [parent[conflictEdge[1]], conflictEdge[1]]
            else:
                return [conflictEdge[0], conflictEdge[1]]
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
int* ancestor;

int find(int index) {
    return index == ancestor[index] ? index : (ancestor[index] = find(ancestor[index]));
}

void merge(int u, int v) {
    ancestor[find(u)] = find(v);
}

int* findRedundantDirectedConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize) {
    int n = edgesSize;
    ancestor = malloc(sizeof(int) * (n + 1));
    for (int i = 1; i <= n; ++i) {
        ancestor[i] = i;
    }
    int parent[n + 1];
    for (int i = 1; i <= n; ++i) {
        parent[i] = i;
    }
    int conflict = -1;
    int cycle = -1;
    for (int i = 0; i < n; ++i) {
        int node1 = edges[i][0], node2 = edges[i][1];
        if (parent[node2] != node2) {
            conflict = i;
        } else {
            parent[node2] = node1;
            if (find(node1) == find(node2)) {
                cycle = i;
            } else {
                merge(node1, node2);
            }
        }
    }
    int* redundant = malloc(sizeof(int) * 2);
    *returnSize = 2;
    if (conflict < 0) {
        redundant[0] = edges[cycle][0], redundant[1] = edges[cycle][1];
        return redundant;
    } else {
        int* conflictEdge = edges[conflict];
        if (cycle >= 0) {
            redundant[0] = parent[conflictEdge[1]], redundant[1] = conflictEdge[1];
            return redundant;
        } else {
            redundant[0] = conflictEdge[0], redundant[1] = conflictEdge[1];
            return redundant;
        }
    }
    return redundant;
}

复杂度分析

  • 时间复杂度：O(n \log n)，其中 n 是图中的节点个数。需要遍历图中的 n 条边，对于每条边，需要对两个节点查找祖先，如果两个节点的祖先不同则需要进行合并，需要进行 2 次查找和最多 1 次合并。一共需要进行 2n 次查找和最多 n 次合并，因此总时间复杂度是 O(2n \log n)=O(n \log n)。这里的并查集使用了路径压缩，但是没有使用按秩合并，最坏情况下的时间复杂度是 O(n \log n)，平均情况下的时间复杂度依然是 O(n \alpha (n))，其中 \alpha 为阿克曼函数的反函数，\alpha (n) 可以认为是一个很小的常数。

  • 空间复杂度：O(n)，其中 n 是图中的节点个数。使用数组 parent 记录每个节点的父节点，并查集使用数组记录每个节点的祖先。

 Comments
On this page
0685-冗余连接 II