在二维平面上的 x 轴上,放置着一些方块。
给你一个二维整数数组 positions ,其中 positions[i] = [lefti, sideLengthi] 表示:第 i
个方块边长为 sideLengthi ,其左侧边与 x 轴上坐标点 lefti 对齐。
每个方块都从一个比目前所有的落地方块更高的高度掉落而下。方块沿 y 轴负方向下落,直到着陆到 另一个正方形的顶边 或者是 x 轴上
。一个方块仅仅是擦过另一个方块的左侧边或右侧边不算着陆。一旦着陆,它就会固定在原地,无法移动。
在每个方块掉落后,你必须记录目前所有已经落稳的 方块堆叠的最高高度 。
返回一个整数数组 ans ,其中 ans[i] 表示在第 i 块方块掉落后堆叠的最高高度。
示例 1:

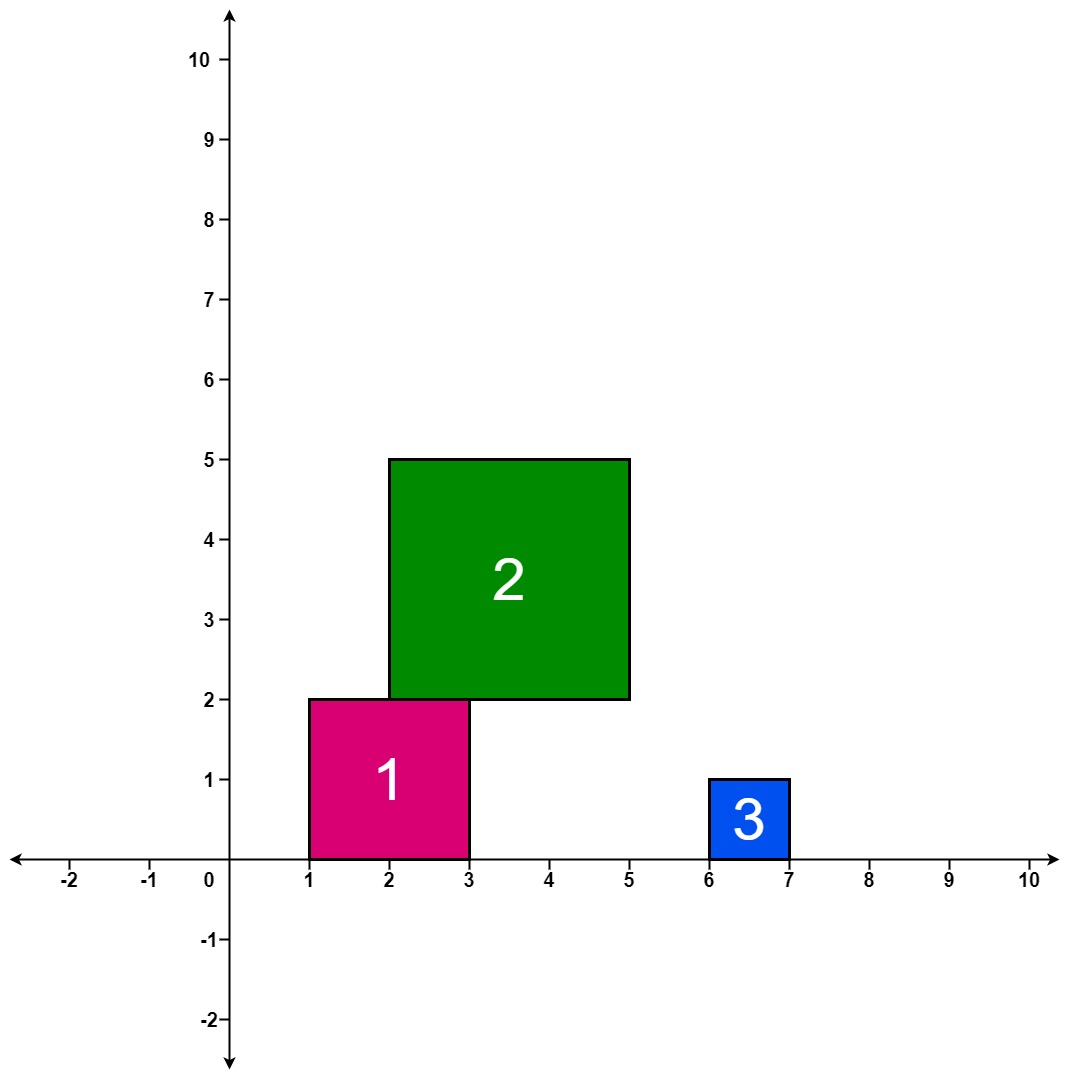
**输入:** positions = [[1,2],[2,3],[6,1]]
**输出:** [2,5,5]
**解释:**
第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 2 。
第 2 个方块掉落后,最高的堆叠由方块 1 和 2 组成,堆叠的最高高度为 5 。
第 3 个方块掉落后,最高的堆叠仍然由方块 1 和 2 组成,堆叠的最高高度为 5 。
因此,返回 [2, 5, 5] 作为答案。
示例 2:
**输入:** positions = [[100,100],[200,100]]
**输出:** [100,100]
**解释:**
第 1 个方块掉落后,最高的堆叠由方块 1 组成,堆叠的最高高度为 100 。
第 2 个方块掉落后,最高的堆叠可以由方块 1 组成也可以由方块 2 组成,堆叠的最高高度为 100 。
因此,返回 [100, 100] 作为答案。
注意,方块 2 擦过方块 1 的右侧边,但不会算作在方块 1 上着陆。
提示:
1 <= positions.length <= 10001 <= lefti <= 1081 <= sideLengthi <= 106
方法一:暴力枚举
我们用数组 heights 记录各个方块掉落后的高度。对于第 i 个掉落的方块,如果它的底部区间与第 j 个掉落的方块有重叠,那么它掉落后的高度至少为 heights}[j] + \textit{size}_i,其中 j \lt i 且 size}_i 为第 i 个掉落的方块的边长。因此对于第 i 个掉落的方块,heights}[i] 的初始值为 size}_i,我们暴力枚举所有之前已经掉落的方块,如果两者的底部区间有重叠,那么更新 heights}[i] = \max(\textit{heights}[i], \textit{heights}[j] + \textit{size}_i)。
因为题目要求返回一个所有已经落稳的方块的最大堆叠高度列表,我们从 i=1 开始,更新 heights}[i] = \max(\textit{heights}[i], \textit{heights}[i - 1]),然后返回 heights 即可。
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
| class Solution:
def fallingSquares(self, positions: List[List[int]]) -> List[int]:
n = len(positions)
heights = [0] * n
for i, (left1, side1) in enumerate(positions):
right1 = left1 + side1 - 1
heights[i] = side1
for j in range(i):
left2, right2 = positions[j][0], positions[j][0] + positions[j][1] - 1
if right1 >= left2 and right2 >= left1:
heights[i] = max(heights[i], heights[j] + side1)
for i in range(1, n):
heights[i] = max(heights[i], heights[i - 1])
return heights
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
int n = positions.size();
vector<int> heights(n);
for (int i = 0; i < n; i++) {
int left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
heights[i] = positions[i][1];
for (int j = 0; j < i; j++) {
int left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
if (right1 >= left2 && right2 >= left1) {
heights[i] = max(heights[i], heights[j] + positions[i][1]);
}
}
}
for (int i = 1; i < n; i++) {
heights[i] = max(heights[i], heights[i - 1]);
}
return heights;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public List<Integer> fallingSquares(int[][] positions) {
int n = positions.length;
List<Integer> heights = new ArrayList<Integer>();
for (int i = 0; i < n; i++) {
int left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
int height = positions[i][1];
for (int j = 0; j < i; j++) {
int left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
if (right1 >= left2 && right2 >= left1) {
height = Math.max(height, heights.get(j) + positions[i][1]);
}
}
heights.add(height);
}
for (int i = 1; i < n; i++) {
heights.set(i, Math.max(heights.get(i), heights.get(i - 1)));
}
return heights;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| public class Solution {
public IList<int> FallingSquares(int[][] positions) {
int n = positions.Length;
IList<int> heights = new List<int>();
for (int i = 0; i < n; i++) {
int left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
heights.Add(positions[i][1]);
for (int j = 0; j < i; j++) {
int left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
if (right1 >= left2 && right2 >= left1) {
heights[i] = Math.Max(heights[i], heights[j] + positions[i][1]);
}
}
}
for (int i = 1; i < n; i++) {
heights[i] = Math.Max(heights[i], heights[i - 1]);
}
return heights;
}
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| #define MAX(a, b) ((a) > (b) ? (a) : (b))
int* fallingSquares(int** positions, int positionsSize, int* positionsColSize, int* returnSize) {
int *heights = (int *)malloc(sizeof(int) * positionsSize);
for (int i = 0; i < positionsSize; i++) {
int left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
heights[i] = positions[i][1];
for (int j = 0; j < i; j++) {
int left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
if (right1 >= left2 && right2 >= left1) {
heights[i] = MAX(heights[i], heights[j] + positions[i][1]);
}
}
}
for (int i = 1; i < positionsSize; i++) {
heights[i] = MAX(heights[i], heights[i - 1]);
}
*returnSize = positionsSize;
return heights;
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| func fallingSquares(positions [][]int) []int {
n := len(positions)
heights := make([]int, n)
for i, p := range positions {
left1, right1 := p[0], p[0]+p[1]-1
heights[i] = p[1]
for j, q := range positions[:i] {
left2, right2 := q[0], q[0]+q[1]-1
if right1 >= left2 && right2 >= left1 {
heights[i] = max(heights[i], heights[j]+p[1])
}
}
}
for i := 1; i < n; i++ {
heights[i] = max(heights[i], heights[i-1])
}
return heights
}
func max(a, b int) int {
if b > a {
return b
}
return a
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| var fallingSquares = function(positions) {
const n = positions.length;
const heights = [];
for (let i = 0; i < n; i++) {
let left1 = positions[i][0], right1 = positions[i][0] + positions[i][1] - 1;
let height = positions[i][1];
for (let j = 0; j < i; j++) {
let left2 = positions[j][0], right2 = positions[j][0] + positions[j][1] - 1;
if (right1 >= left2 && right2 >= left1) {
height = Math.max(height, heights[j] + positions[i][1]);
}
}
heights.push(height);
}
for (let i = 1; i < n; i++) {
heights.splice(i, 1, Math.max(heights[i], heights[i - 1]));
}
return heights;
};
|
复杂度分析
方法二:有序集合
已经落稳的方块的堆叠高度情况可以使用一个有序集合 heightMap 进行记录,heightMap}[x_1] 表示从 x_1 开始(包括 x_1)直到遇到下一个 x_2(不包括 x_2)的所有数轴上的点的堆叠高度为 heightMap}[x_1],其中 x_2 > x_1。通俗上来说就是用 heightMap 记录每一个相对于前一个点而言,堆叠高度发生变化的点。初始时,令 heightMap}[0] = 0,表示从 0 开始的所有点的堆叠高度都为 0。
对于第 i 个掉落的方块,记它底部的左端点为 left,右端点为 right。我们在有序集合中查找该区间 [\textit{left}, \textit{right}] 内所有点的堆叠高度,然后更新该方块对应的堆叠高度 height。在第 i 个方块掉落后,区间 [\textit{left}, \textit{right}] 内的所有点的堆叠高度都是 height,因此我们将有序集合里对应区间 [\textit{left}, \textit{right}] 内的点全部删除。该掉落的方块带来的堆叠高度变化主要在两个点,即 left 和 right} + 1,更新对应的变化即可。
前 i 个掉落的方块的最大堆叠高度等于前 i - 1 个掉落的方块的最大堆叠高度与第 i 个方块的堆叠高度的最大值。
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public:
vector<int> fallingSquares(vector<vector<int>>& positions) {
int n = positions.size();
vector<int> ret(n);
map<int, int> heightMap;
heightMap[0] = 0;
for (int i = 0; i < n; i++) {
int size = positions[i][1];
int left = positions[i][0], right = positions[i][0] + positions[i][1] - 1;
auto lp = heightMap.upper_bound(left), rp = heightMap.upper_bound(right);
int rHeight = prev(rp)->second;
int height = 0;
for (auto p = prev(lp); p != rp; p++) {
height = max(height, p->second + size);
}
heightMap.erase(lp, rp);
heightMap[left] = height;
if (rp == heightMap.end() || rp->first != right + 1) {
heightMap[right + 1] = rHeight;
}
ret[i] = i > 0 ? max(ret[i - 1], height) : height;
}
return ret;
}
};
|
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| class Solution {
public List<Integer> fallingSquares(int[][] positions) {
int n = positions.length;
List<Integer> ret = new ArrayList<Integer>();
TreeMap<Integer, Integer> heightMap = new TreeMap<Integer, Integer>();
heightMap.put(0, 0);
for (int i = 0; i < n; i++) {
int size = positions[i][1];
int left = positions[i][0], right = positions[i][0] + positions[i][1] - 1;
Integer lp = heightMap.higherKey(left), rp = heightMap.higherKey(right);
Integer prevRightKey = rp != null ? heightMap.lowerKey(rp) : heightMap.lastKey();
int rHeight = prevRightKey != null ? heightMap.get(prevRightKey) : 0;
int height = 0;
Integer prevLeftKey = lp != null ? heightMap.lowerKey(lp) : heightMap.lastKey();
Map<Integer, Integer> tail = prevLeftKey != null ? heightMap.tailMap(prevLeftKey) : heightMap;
for (Map.Entry<Integer, Integer> entry : tail.entrySet()) {
if (entry.getKey() == rp) {
break;
}
height = Math.max(height, entry.getValue() + size);
}
Set<Integer> keySet = new TreeSet<Integer>(tail.keySet());
for (Integer tmp : keySet) {
if (lp == null || tmp < lp) {
continue;
}
if (rp != null && tmp >= rp) {
break;
}
heightMap.remove(tmp);
}
heightMap.put(left, height);
if (rp == null || rp != right + 1) {
heightMap.put(right + 1, rHeight);
}
ret.add(i > 0 ? Math.max(ret.get(i - 1), height) : height);
}
return ret;
}
}
|
复杂度分析
时间复杂度:O(n \log n),其中 n 是数组 positions 的长度。有序集合 heightMap 最多插入 2n + 1 个元素,因此整个循环最多执行删除操作 2n + 1 次,而每次循环里的查询操作只比删除操作多一次,因此总的查询操作最多为 3n + 1 次;插入操作、删除操作、迭代器递增操作以及二分查找操作都需要 O(\log n),因此总共需要 O(n \log n)。
空间复杂度:O(n)。有序集合最多保存 2n + 1 个元素。