0736-Lisp 语法解析

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

给你一个类似 Lisp 语句的字符串表达式 expression，求出其计算结果。

表达式语法如下所示:

  • 表达式可以为整数， let 表达式， add 表达式， mult 表达式，或赋值的变量。表达式的结果总是一个整数。
  • (整数可以是正整数、负整数、0)
  • let 表达式采用 "(let v1 e1 v2 e2 ... vn en expr)" 的形式，其中 let 总是以字符串 "let"来表示，接下来会跟随一对或多对交替的变量和表达式，也就是说，第一个变量 v1被分配为表达式 e1 的值，第二个变量 v2 被分配为表达式 e2 的值， 依次类推 ；最终 let 表达式的值为 expr表达式的值。
  • add 表达式表示为 "(add e1 e2)" ，其中 add 总是以字符串 "add" 来表示，该表达式总是包含两个表达式 e1、e2 ，最终结果是 e1 表达式的值与 e2 表达式的值之 和 。
  • mult 表达式表示为 "(mult e1 e2)" ，其中 mult 总是以字符串 "mult" 表示，该表达式总是包含两个表达式 e1、e2，最终结果是 e1 表达式的值与 e2 表达式的值之 积 。
  • 在该题目中，变量名以小写字符开始，之后跟随 0 个或多个小写字符或数字。为了方便，"add" ，"let" ，"mult" 会被定义为 “关键字” ，不会用作变量名。
  • 最后，要说一下作用域的概念。计算变量名所对应的表达式时，在计算上下文中，首先检查最内层作用域（按括号计），然后按顺序依次检查外部作用域。测试用例中每一个表达式都是合法的。有关作用域的更多详细信息，请参阅示例。

示例 1：

**输入：** expression = "(let x 2 (mult x (let x 3 y 4 (add x y))))"
**输出：** 14
**解释：**
计算表达式 (add x y), 在检查变量 x 值时，
在变量的上下文中由最内层作用域依次向外检查。
首先找到 x = 3, 所以此处的 x 值是 3 。

示例 2：

**输入：** expression = "(let x 3 x 2 x)"
**输出：** 2
**解释：** let 语句中的赋值运算按顺序处理即可。

示例 3：

**输入：** expression = "(let x 1 y 2 x (add x y) (add x y))"
**输出：** 5
**解释：**
第一个 (add x y) 计算结果是 3，并且将此值赋给了 x 。 
第二个 (add x y) 计算结果是 3 + 2 = 5 。

提示：

  • 1 <= expression.length <= 2000
  • exprssion 中不含前导和尾随空格
  • expressoin 中的不同部分（token）之间用单个空格进行分隔
  • 答案和所有中间计算结果都符合 32-bit 整数范围
  • 测试用例中的表达式均为合法的且最终结果为整数

方法一：递归解析

对于一个表达式 expression，如果它的首字符不等于左括号 `(‘，那么它只能是一个整数或者变量；否则它是 let，add 和 mult 三种表达式之一。

定义函数 parseVar 用来解析变量以及函数 parseInt 用来解析整数。使用 scope 来记录作用域，每个变量都依次记录下它从外到内的所有值，查找时只需要查找最后一个数值。我们递归地解析表达式 expression。

  • expression 的下一个字符不等于左括号 `(‘。

    • expression 的下一个字符是小写字母，那么表达式是一个变量，使用函数 parseVar 解析变量，然后在 scope 中查找变量的最后一个数值即最内层作用域的值并返回结果。

    • expression 的下一个字符不是小写字母，那么表达式是一个整数，使用函数 parseInt 解析并返回结果。

  • 去掉左括号后，expression 的下一个字符是 `l’，那么表达式是 let 表达式。对于 let 表达式，需要判断是否已经解析到最后一个 expr 表达式。

    • 如果下一个字符不是小写字母，或者解析变量后下一个字符是右括号 `)’，说明是最后一个 expr 表达式，计算它的值并返回结果。并且我们需要在 scope 中清除 let 表达式对应的作用域变量。

    • 否则说明是交替的变量 v_i 和表达式 e_i，在 scope 将变量 v_i 的数值列表增加表达式 e_i 的数值。

  • 去掉左括号后，expression 的下一个字符是 `a’，那么表达式是 add 表达式。计算 add 表达式对应的两个表达式 e_1 和 e_2 的值，返回两者之和。

  • 去掉左括号后，expression 的下一个字符是 `m’，那么表达式是 mult 表达式。计算 mult 表达式对应的两个表达式 e_1 和 e_2 的值，返回两者之积。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
class Solution:
    def evaluate(self, expression: str) -> int:
        i, n = 0, len(expression)

        def parseVar() -> str:
            nonlocal i
            i0 = i
            while i < n and expression[i] != ' ' and expression[i] != ')':
                i += 1
            return expression[i0:i]

        def parseInt() -> int:
            nonlocal i
            sign, x = 1, 0
            if expression[i] == '-':
                sign = -1
                i += 1
            while i < n and expression[i].isdigit():
                x = x * 10 + int(expression[i])
                i += 1
            return sign * x

        scope = defaultdict(list)

        def innerEvaluate() -> int:
            nonlocal i
            if expression[i] != '(':  # 非表达式，可能为：整数或变量
                if expression[i].islower():  # 变量
                    return scope[parseVar()][-1]
                return parseInt()  # 整数
            i += 1  # 移除左括号
            if expression[i] == 'l':  # "let" 表达式
                i += 4  # 移除 "let "
                vars = []
                while True:
                    if not expression[i].islower():
                        ret = innerEvaluate()  # let 表达式的最后一个 expr 表达式的值
                        break
                    var = parseVar()
                    if expression[i] == ')':
                        ret = scope[var][-1]  # let 表达式的最后一个 expr 表达式的值
                        break
                    vars.append(var)
                    i += 1  # 移除空格
                    scope[var].append(innerEvaluate())
                    i += 1  # 移除空格
                for var in vars:
                    scope[var].pop()  # 清除当前作用域的变量
            elif expression[i] == 'a':  # "add" 表达式
                i += 4  # 移除 "add "
                e1 = innerEvaluate()
                i += 1  # 移除空格
                e2 = innerEvaluate()
                ret = e1 + e2
            else:  # "mult" 表达式
                i += 5  # 移除 "mult "
                e1 = innerEvaluate()
                i += 1  # 移除空格
                e2 = innerEvaluate()
                ret = e1 * e2
            i += 1  # 移除右括号
            return ret

        return innerEvaluate()
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
class Solution {
private:
    unordered_map<string, vector<int>> scope;

public:
    int evaluate(string expression) {
        int start = 0;
        return innerEvaluate(expression, start);
    }

    int innerEvaluate(const string &expression, int &start) {
        if (expression[start] != '(') { // 非表达式，可能为：整数或变量
            if (islower(expression[start])) {
                string var = parseVar(expression, start); // 变量
                return scope[var].back();
            } else { // 整数
                return parseInt(expression, start);
            }
        }
        int ret;
        start++; // 移除左括号
        if (expression[start] == 'l') { // "let" 表达式
            start += 4; // 移除 "let "
            vector<string> vars;
            while (true) {
                if (!islower(expression[start])) {
                    ret = innerEvaluate(expression, start); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                string var = parseVar(expression, start);
                if (expression[start] == ')') {
                    ret = scope[var].back(); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                vars.push_back(var);
                start++; // 移除空格
                int e = innerEvaluate(expression, start);
                scope[var].push_back(e);
                start++; // 移除空格
            }
            for (auto var : vars) {
                scope[var].pop_back(); // 清除当前作用域的变量
            }
        } else if (expression[start] == 'a') { // "add" 表达式
            start += 4; // 移除 "add "
            int e1 = innerEvaluate(expression, start);
            start++; // 移除空格
            int e2 = innerEvaluate(expression, start);
            ret = e1 + e2;
        } else { // "mult" 表达式
            start += 5; // 移除 "mult "
            int e1 = innerEvaluate(expression, start);
            start++; // 移除空格
            int e2 = innerEvaluate(expression, start);
            ret = e1 * e2;
        }
        start++; // 移除右括号
        return ret;
    }

    int parseInt(const string &expression, int &start) { // 解析整数
        int n = expression.size();
        int ret = 0, sign = 1;
        if (expression[start] == '-') {
            sign = -1;
            start++;
        }
        while (start < n && isdigit(expression[start])) {
            ret = ret * 10 + (expression[start] - '0');
            start++;
        }
        return sign * ret;
    }

    string parseVar(const string &expression, int &start) { // 解析变量
        int n = expression.size();
        string ret;
        while (start < n && expression[start] != ' ' && expression[start] != ')') {
            ret.push_back(expression[start]);
            start++;
        }
        return ret;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
class Solution {
    Map<String, Deque<Integer>> scope = new HashMap<String, Deque<Integer>>();
    int start = 0;

    public int evaluate(String expression) {
        return innerEvaluate(expression);
    }

    public int innerEvaluate(String expression) {
        if (expression.charAt(start) != '(') { // 非表达式，可能为：整数或变量
            if (Character.isLowerCase(expression.charAt(start))) {
                String var = parseVar(expression); // 变量
                return scope.get(var).peek();
            } else { // 整数
                return parseInt(expression);
            }
        }
        int ret;
        start++; // 移除左括号
        if (expression.charAt(start) == 'l') { // "let" 表达式
            start += 4; // 移除 "let "
            List<String> vars = new ArrayList<String>();
            while (true) {
                if (!Character.isLowerCase(expression.charAt(start))) {
                    ret = innerEvaluate(expression); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                String var = parseVar(expression);
                if (expression.charAt(start) == ')') {
                    ret = scope.get(var).peek(); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                vars.add(var);
                start++; // 移除空格
                int e = innerEvaluate(expression);
                scope.putIfAbsent(var, new ArrayDeque<Integer>());
                scope.get(var).push(e);
                start++; // 移除空格
            }
            for (String var : vars) {
                scope.get(var).pop(); // 清除当前作用域的变量
            }
        } else if (expression.charAt(start) == 'a') { // "add" 表达式
            start += 4; // 移除 "add "
            int e1 = innerEvaluate(expression);
            start++; // 移除空格
            int e2 = innerEvaluate(expression);
            ret = e1 + e2;
        } else { // "mult" 表达式
            start += 5; // 移除 "mult "
            int e1 = innerEvaluate(expression);
            start++; // 移除空格
            int e2 = innerEvaluate(expression);
            ret = e1 * e2;
        }
        start++; // 移除右括号
        return ret;
    }

    public int parseInt(String expression) { // 解析整数
        int n = expression.length();
        int ret = 0, sign = 1;
        if (expression.charAt(start) == '-') {
            sign = -1;
            start++;
        }
        while (start < n && Character.isDigit(expression.charAt(start))) {
            ret = ret * 10 + (expression.charAt(start) - '0');
            start++;
        }
        return sign * ret;
    }

    public String parseVar(String expression) { // 解析变量
        int n = expression.length();
        StringBuffer ret = new StringBuffer();
        while (start < n && expression.charAt(start) != ' ' && expression.charAt(start) != ')') {
            ret.append(expression.charAt(start));
            start++;
        }
        return ret.toString();
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
public class Solution {
    Dictionary<string, Stack<int>> scope = new Dictionary<string, Stack<int>>();
    int start = 0;

    public int Evaluate(string expression) {
        return InnerEvaluate(expression);
    }

    public int InnerEvaluate(string expression) {
        if (expression[start] != '(') { // 非表达式，可能为：整数或变量
            if (char.IsLower(expression[start])) {
                string var = ParseVar(expression); // 变量
                return scope[var].Peek();
            } else { // 整数
                return ParseInt(expression);
            }
        }
        int ret;
        start++; // 移除左括号
        if (expression[start] == 'l') { // "let" 表达式
            start += 4; // 移除 "let "
            IList<string> vars = new List<string>();
            while (true) {
                if (!char.IsLower(expression[start])) {
                    ret = InnerEvaluate(expression); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                string var = ParseVar(expression);
                if (expression[start] == ')') {
                    ret = scope[var].Peek(); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                vars.Add(var);
                start++; // 移除空格
                int e = InnerEvaluate(expression);
                if (!scope.ContainsKey(var)) {
                    scope.Add(var, new Stack<int>());
                }
                scope[var].Push(e);
                start++; // 移除空格
            }
            foreach (string var in vars) {
                scope[var].Pop(); // 清除当前作用域的变量
            }
        } else if (expression[start] == 'a') { // "add" 表达式
            start += 4; // 移除 "add "
            int e1 = InnerEvaluate(expression);
            start++; // 移除空格
            int e2 = InnerEvaluate(expression);
            ret = e1 + e2;
        } else { // "mult" 表达式
            start += 5; // 移除 "mult "
            int e1 = InnerEvaluate(expression);
            start++; // 移除空格
            int e2 = InnerEvaluate(expression);
            ret = e1 * e2;
        }
        start++; // 移除右括号
        return ret;
    }

    public int ParseInt(string expression) { // 解析整数
        int n = expression.Length;
        int ret = 0, sign = 1;
        if (expression[start] == '-') {
            sign = -1;
            start++;
        }
        while (start < n && char.IsDigit(expression[start])) {
            ret = ret * 10 + (expression[start] - '0');
            start++;
        }
        return sign * ret;
    }

    public string ParseVar(string expression) { // 解析变量
        int n = expression.Length;
        StringBuilder ret = new StringBuilder();
        while (start < n && expression[start] != ' ' && expression[start] != ')') {
            ret.Append(expression[start]);
            start++;
        }
        return ret.ToString();
    }
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
typedef struct {
    char *key;
    struct ListNode *lst;
    UT_hash_handle hh;
} HashItem;

typedef struct Node {
    char *var;
    struct Node *next;
} Node;

HashItem *scope = NULL;

int parseInt(const char *expression, int *start) { // 解析整数
    int n = strlen(expression);
    int ret = 0, sign = 1;
    if (expression[*start] == '-') {
        sign = -1;
        (*start)++;
    }
    while ((*start) < n && isdigit(expression[*start])) {
        ret = ret * 10 + (expression[*start] - '0');
        (*start)++;
    }
    return sign * ret;
}

char *parseVar(const char *expression, int *start) { // 解析变量
    int n = strlen(expression);
    char *ret = (char *)malloc(sizeof(char) * (n - (*start) + 1));
    int pos = 0;
    while ((*start) < n && expression[*start] != ' ' && expression[*start] != ')') {
        ret[pos++] = expression[(*start)++];
    }
    ret[pos] = '\0';
    return ret;
}

int innerEvaluate(const char *expression, int *start) {
    if (expression[*start] != '(') { // 非表达式，可能为：整数或变量
        if (islower(expression[*start])) {
            char *var = parseVar(expression, start); // 变量
            HashItem *pEntry = NULL;
            HASH_FIND_STR(scope, var, pEntry);
            free(var);
            return pEntry->lst->val;
        } else { // 整数
            return parseInt(expression, start);
        }
    }
    int ret;
    (*start)++; // 移除左括号
    if (expression[*start] == 'l') { // "let" 表达式
        (*start) += 4; // 移除 "let "
        Node *vars = NULL;
        while (true) {
            if (isdigit(expression[*start]) || expression[*start] == '(') {
                ret = innerEvaluate(expression, start); // let 表达式的最后一个 expr 表达式的值
                break;
            }
            char *var = parseVar(expression, start);
            if (expression[*start] == ')') {
                int start1 = 0;
                ret = innerEvaluate(var, &start1); // let 表达式的最后一个 expr 表达式的值
                break;
            }
            Node *node = (Node *)malloc(sizeof(Node));
            node->var = var;
            node->next = vars;
            vars = node;
            (*start)++; // 移除空格
            int e = innerEvaluate(expression, start);
            HashItem *pEntry = NULL;
            HASH_FIND_STR(scope, var, pEntry);
            if (NULL == pEntry) {
                pEntry = (HashItem *)malloc(sizeof(HashItem));
                pEntry->key = var;
                pEntry->lst = NULL;
                HASH_ADD_STR(scope, key, pEntry);
            }
            struct ListNode *pNode = (struct ListNode *)malloc(sizeof(struct ListNode));
            pNode->val = e;
            pNode->next = pEntry->lst;
            pEntry->lst = pNode; 
            (*start)++; // 移除空格
        }
        for (Node *node = vars; node; node = node->next) {
            HashItem *pEntry = NULL;
            HASH_FIND_STR(scope, node->var, pEntry);
            if (pEntry) {
                struct ListNode *pNode = pEntry->lst; // 清除当前作用域的变量
                pEntry->lst = pEntry->lst->next;
                free(pNode);
            }
        }
    } else if (expression[*start] == 'a') { // "add" 表达式
        (*start) += 4; // 移除 "add "
        int e1 = innerEvaluate(expression, start);
        (*start)++; // 移除空格
        int e2 = innerEvaluate(expression, start);
        ret = e1 + e2;
    } else { // "mult" 表达式
        (*start) += 5; // 移除 "mult "
        int e1 = innerEvaluate(expression, start);
        (*start)++; // 移除空格
        int e2 = innerEvaluate(expression, start);
        ret = e1 * e2;
    }
    (*start)++; // 移除右括号
    return ret;
}

void freeScope() {
    HashItem *curr, *tmp;
    HASH_ITER(hh, scope, curr, tmp) {
      HASH_DEL(scope, curr);
      free(curr->key);
      for (struct ListNode *node = curr->lst; node; ) {
          struct ListNode *pNode = node;
          node = node->next;
          free(pNode);
      }
      free(curr);
    }
}

int evaluate(char * expression){
    int start = 0;    
    int ret = innerEvaluate(expression, &start);
    freeScope();
    return ret;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
func evaluate(expression string) int {
    i, n := 0, len(expression)
    parseVar := func() string {
        i0 := i
        for i < n && expression[i] != ' ' && expression[i] != ')' {
            i++
        }
        return expression[i0:i]
    }
    parseInt := func() int {
        sign, x := 1, 0
        if expression[i] == '-' {
            sign = -1
            i++
        }
        for i < n && unicode.IsDigit(rune(expression[i])) {
            x = x*10 + int(expression[i]-'0')
            i++
        }
        return sign * x
    }

    scope := map[string][]int{}
    var innerEvaluate func() int
    innerEvaluate = func() (ret int) {
        if expression[i] != '(' { // 非表达式，可能为：整数或变量
            if unicode.IsLower(rune(expression[i])) { // 变量
                vals := scope[parseVar()]
                return vals[len(vals)-1]
            }
            return parseInt() // 整数
        }
        i++ // 移除左括号
        if expression[i] == 'l' { // "let" 表达式
            i += 4 // 移除 "let "
            vars := []string{}
            for {
                if !unicode.IsLower(rune(expression[i])) {
                    ret = innerEvaluate() // let 表达式的最后一个 expr 表达式的值
                    break
                }
                vr := parseVar()
                if expression[i] == ')' {
                    vals := scope[vr]
                    ret = vals[len(vals)-1] // let 表达式的最后一个 expr 表达式的值
                    break
                }
                vars = append(vars, vr)
                i++ // 移除空格
                scope[vr] = append(scope[vr], innerEvaluate())
                i++ // 移除空格
            }
            for _, vr := range vars {
                scope[vr] = scope[vr][:len(scope[vr])-1] // 清除当前作用域的变量
            }
        } else if expression[i] == 'a' { // "add" 表达式
            i += 4 // 移除 "add "
            e1 := innerEvaluate()
            i++ // 移除空格
            e2 := innerEvaluate()
            ret = e1 + e2
        } else { // "mult" 表达式
            i += 5 // 移除 "mult "
            e1 := innerEvaluate()
            i++ // 移除空格
            e2 := innerEvaluate()
            ret = e1 * e2
        }
        i++ // 移除右括号
        return
    }
    return innerEvaluate()
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
var evaluate = function(expression) {
    const scope = new Map();
    let start = 0;

    const innerEvaluate = (expression) => {
        if (expression[start] !== '(') { // 非表达式，可能为：整数或变量
            if (isLowerCase(expression[start])) {
                const v = parseVar(expression); // 变量
                const n = scope.get(v).length;
                return scope.get(v)[n - 1];
            } else { // 整数
                return parseInt(expression);
            }
        }
        let ret;
        start++; // 移除左括号
        if (expression[start] === 'l') { // "let" 表达式
            start += 4; // 移除 "let "
            const vars = [];
            while (true) {
                if (!isLowerCase(expression[start])) {
                    ret = innerEvaluate(expression); // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                const v = parseVar(expression);
                if (expression[start] === ')') {
                    const n = scope.get(v).length;
                    ret = scope.get(v)[n - 1]; // let 表达式的最后一个 expr 表达式的值
                    break;
                }
                vars.push(v);
                start++; // 移除空格
                const e = innerEvaluate(expression);
                if (!scope.has(v)) {
                    scope.set(v, []);
                }
                scope.get(v).push(e);
                start++; // 移除空格
            }
            for (const v of vars) {
                scope.get(v).pop(); // 清除当前作用域的变量
            }
        } else if (expression[start] === 'a') { // "add" 表达式
            start += 4; // 移除 "add "
            const e1 = innerEvaluate(expression);
            start++; // 移除空格
            const e2 = innerEvaluate(expression);
            ret = e1 + e2;
        } else { // "mult" 表达式
            start += 5; // 移除 "mult "
            const e1 = innerEvaluate(expression);
            start++; // 移除空格
            const e2 = innerEvaluate(expression);
            ret = e1 * e2;
        }
        start++; // 移除右括号
        return ret;
    }

    const parseInt = (expression) => { // 解析整数
        const n = expression.length;
        let ret = 0, sign = 1;
        if (expression[start] === '-') {
            sign = -1;
            start++;
        }
        while (start < n && isDigit(expression[start])) {
            ret = ret * 10 + (expression.charAt(start) - '0');
            start++;
        }
        return sign * ret;
    }

    const parseVar = (expression) => { // 解析变量
        const n = expression.length;
        let ret = '';
        while (start < n && expression[start] !== ' ' && expression[start] !== ')') {
            ret += expression[start];
            start++;
        }
        return ret;
    }

    return innerEvaluate(expression, start);
};

const isDigit = (ch) => {
    return parseFloat(ch).toString() === "NaN" ? false : true;
}

const isLowerCase = (ch) => {
    return ch >= 'a' && ch <= 'z';
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 expression 的长度。递归调用函数 innerEvaluate 在某一层调用的时间复杂度为 O(k)，其中 k 为指针 start 在该层调用的移动次数。在整个递归调用过程中，指针 start 会遍历整个字符串，因此解析 expression 需要 O(n)。

  • 空间复杂度：O(n)。保存 scope 以及递归调用栈需要 O(n) 的空间。

方法二：状态机

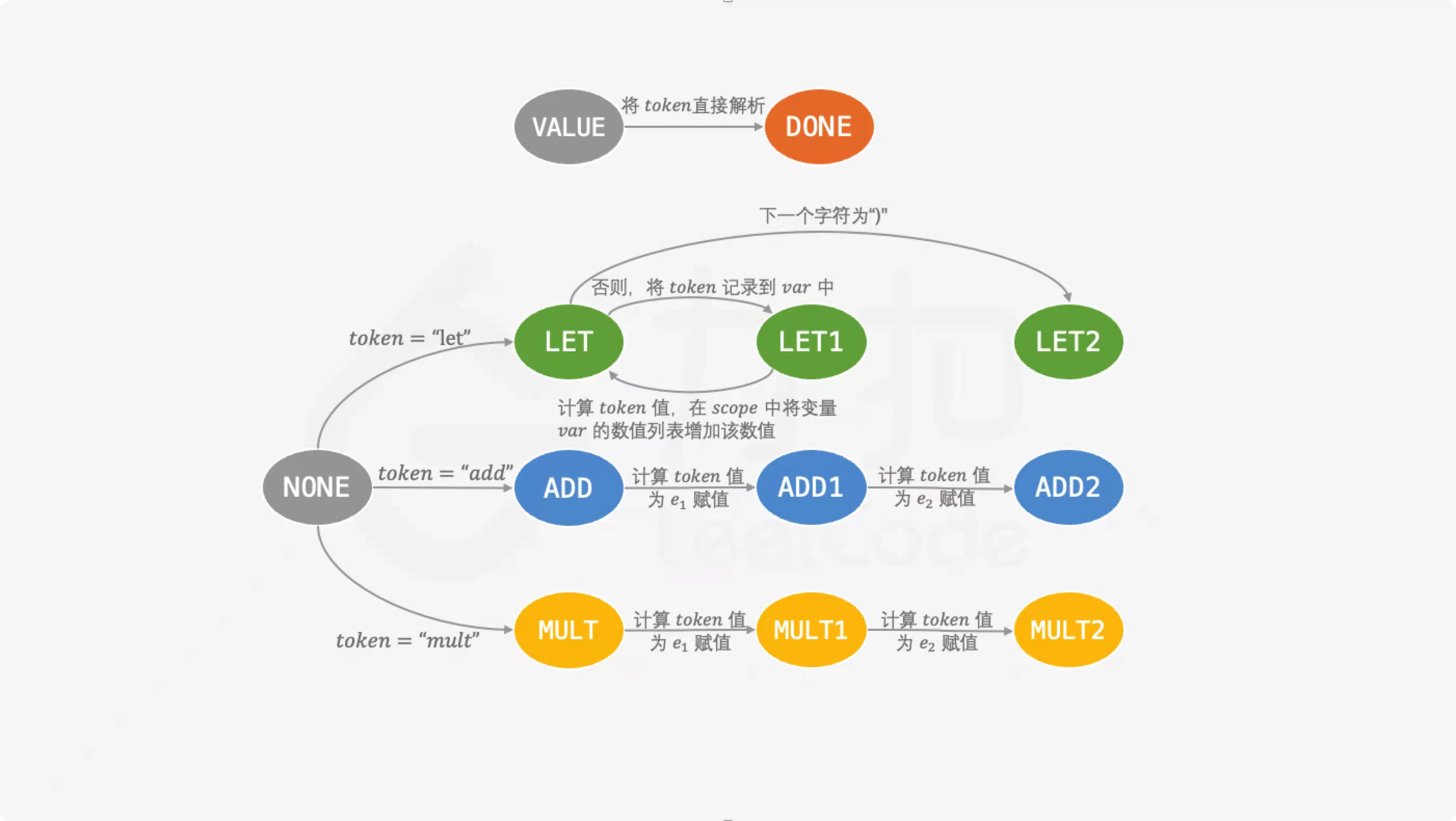
定义状态 ExprStatus，状态机的初始状态 cur 为 VALUE。

当我们解析到一个左括号时，我们需要将当前状态 cur 压入栈中，然后将当前状态 cur 设为状态 NONE，表示对一个未知表达式的解析。当我们解析到一个右括号时，我们需要根据括号对应的表达式的类型来计算最终值，并且将它转换成一个 token 传回上层状态，将上层状态出栈并设为当前状态 cur，对于 let 表达式，我们还需要清除它的作用域。

以下的每次状态的转换都会伴随一个 token，其中 token 表示被空格和括号分隔开的词块，并且 let，add 和 mult 三种表达式都可以转换成一个整数 token。状态转换如下：

  • 状态 VALUE：

    • 将 token 直接解析成整数保存到 value 中，并将状态设为 DONE，标志解析完成。

  • 状态 NONE：

    • token} = \text{``let”：将当前状态 cur 设为 LET。

    • token} = \text{``add”：将当前状态 cur 设为 ADD。

    • token} = \text{``mult”：将当前状态 cur 设为 MULT。

  • 状态 LET：

    • 下一个字符是右括号，说明已经到达 let 表达式的最后一个 expr 表达式，计算 token 的值并保存到 value，并且将当前状态 cur 设为 LET2，标志着 let 表达式的解析完成。

    • 下一个字符不是右括号，将 token 记录到 var 中，并且将当前状态 cur 设为 LET1。

  • 状态 LET1：

    • 计算 token 的值，在 scope 中将变量 var 的数值列表增加该数值，并且将当前状态 cur 设为 LET。

  • 状态 ADD：

    • 计算 token 的值，为 e_1 赋值，并且将当前状态 cur 设为 ADD1。

  • 状态 ADD1：

    • 计算 token 的值，为 e_2 赋值，并且将当前状态 cur 设为 ADD2，标志着 add 表达式的解析完成。

  • 状态 MULT：

    • 计算 token 的值，为 e_1 赋值，并且将当前状态 cur 设为 MULT1。

  • 状态 MULT1：

    • 计算 token 的值，为 e_2 赋值，并且将当前状态 cur 设为 MULT2，标志着 mult 表达式的解析完成。

状态机有两种转换路线，第一种是从 VALUE 到 DONE 的转换路线，第二种是从 NONE 到 LET2，ADD2 或 MULT2 的转换路线。

状态机转换图

代码

[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
from enum import Enum, auto

class ExprStatus(Enum):
    VALUE = auto()  # 初始状态
    NONE  = auto()  # 表达式类型未知
    LET   = auto()  # let 表达式
    LET1  = auto()  # let 表达式已经解析了 vi 变量
    LET2  = auto()  # let 表达式已经解析了最后一个表达式 expr
    ADD   = auto()  # add 表达式
    ADD1  = auto()  # add 表达式已经解析了 e1 表达式
    ADD2  = auto()  # add 表达式已经解析了 e2 表达式
    MULT  = auto()  # mult 表达式
    MULT1 = auto()  # mult 表达式已经解析了 e1 表达式
    MULT2 = auto()  # mult 表达式已经解析了 e2 表达式
    DONE  = auto()  # 解析完成

class Expr:
    __slots__ = 'status', 'var', 'value', 'e1', 'e2'

    def __init__(self, status):
        self.status = status
        self.var = ''  # let 的变量 vi
        self.value = 0  # VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
        self.e1 = self.e2 = 0  # add 或 mult 表达式的两个表达式 e1 和 e2 的数值

class Solution:
    def evaluate(self, expression: str) -> int:
        scope = defaultdict(list)

        def calculateToken(token: str) -> int:
            return scope[token][-1] if token[0].islower() else int(token)

        vars = []
        s = []
        cur = Expr(ExprStatus.VALUE)
        i, n = 0, len(expression)
        while i < n:
            if expression[i] == ' ':
                i += 1  # 去掉空格
                continue
            if expression[i] == '(':
                i += 1  # 去掉左括号
                s.append(cur)
                cur = Expr(ExprStatus.NONE)
                continue
            if expression[i] == ')':  # 本质上是把表达式转成一个 token
                i += 1  # 去掉右括号
                if cur.status is ExprStatus.LET2:
                    token = str(cur.value)
                    for var in vars[-1]:
                        scope[var].pop()  # 清除作用域
                    vars.pop()
                elif cur.status is ExprStatus.ADD2:
                    token = str(cur.e1 + cur.e2)
                else:
                    token = str(cur.e1 * cur.e2)
                cur = s.pop()  # 获取上层状态
            else:
                i0 = i
                while i < n and expression[i] != ' ' and expression[i] != ')':
                    i += 1
                token = expression[i0:i]

            if cur.status is ExprStatus.VALUE:
                cur.value = int(token)
                cur.status = ExprStatus.DONE
            elif cur.status is ExprStatus.NONE:
                if token == "let":
                    cur.status = ExprStatus.LET
                    vars.append([])  # 记录该层作用域的所有变量, 方便后续的清除
                elif token == "add":
                    cur.status = ExprStatus.ADD
                elif token == "mult":
                    cur.status = ExprStatus.MULT
            elif cur.status is ExprStatus.LET:
                if expression[i] == ')':  # let 表达式的最后一个 expr 表达式
                    cur.value = calculateToken(token)
                    cur.status = ExprStatus.LET2
                else:
                    cur.var = token
                    vars[-1].append(token)  # 记录该层作用域的所有变量, 方便后续的清除
                    cur.status = ExprStatus.LET1
            elif cur.status is ExprStatus.LET1:
                scope[cur.var].append(calculateToken(token))
                cur.status = ExprStatus.LET
            elif cur.status is ExprStatus.ADD:
                cur.e1 = calculateToken(token)
                cur.status = ExprStatus.ADD1
            elif cur.status is ExprStatus.ADD1:
                cur.e2 = calculateToken(token)
                cur.status = ExprStatus.ADD2
            elif cur.status is ExprStatus.MULT:
                cur.e1 = calculateToken(token)
                cur.status = ExprStatus.MULT1
            elif cur.status is ExprStatus.MULT1:
                cur.e2 = calculateToken(token)
                cur.status = ExprStatus.MULT2
        return cur.value
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
enum ExprStatus {
    VALUE = 0, // 初始状态
    NONE,      // 表达式类型未知
    LET,       // let 表达式
    LET1,      // let 表达式已经解析了 vi 变量
    LET2,      // let 表达式已经解析了最后一个表达式 expr
    ADD,       // add 表达式
    ADD1,      // add 表达式已经解析了 e1 表达式
    ADD2,      // add 表达式已经解析了 e2 表达式
    MULT,      // mult 表达式
    MULT1,     // mult 表达式已经解析了 e1 表达式
    MULT2,     // mult 表达式已经解析了 e2 表达式
    DONE       // 解析完成
};

struct Expr {
    ExprStatus status;
    string var; // let 的变量 vi
    int value; // VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
    int e1, e2; // add 或 mult 表达式的两个表达式 e1 和 e2 的数值

    Expr(ExprStatus s) {
        status = s;
    }
};

class Solution {
private:
    unordered_map<string, vector<int>> scope;

public:
    int evaluate(string expression) {
        vector<vector<string>> vars;
        int start = 0, n = expression.size();
        stack<Expr> s;
        Expr cur(VALUE);
        while (start < n) {
            if (expression[start] == ' ') {
                start++; // 去掉空格
                continue;
            }
            if (expression[start] == '(') {
                start++; // 去掉左括号
                s.push(cur);
                cur = Expr(NONE);
                continue;
            }
            string token;
            if (expression[start] == ')') { // 本质上是把表达式转成一个 token
                start++; // 去掉右括号
                if (cur.status == LET2) {
                    token = to_string(cur.value);
                    for (auto var : vars.back()) { // 清除作用域
                        scope[var].pop_back();
                    }
                    vars.pop_back();
                } else if (cur.status == ADD2) {
                    token = to_string(cur.e1 + cur.e2);
                } else {
                    token = to_string(cur.e1 * cur.e2);
                }
                cur = s.top(); // 获取上层状态
                s.pop();
            } else {
                while (start < n && expression[start] != ' ' && expression[start] != ')') {
                    token.push_back(expression[start]);
                    start++;
                }
            }
            switch (cur.status) {
                case VALUE:
                    cur.value = stoi(token);
                    cur.status = DONE;
                    break;
                case NONE:
                    if (token == "let") {
                        cur.status = LET;
                        vars.emplace_back(); // 记录该层作用域的所有变量, 方便后续的清除
                    } else if (token == "add") {
                        cur.status = ADD;
                    } else if (token == "mult") {
                        cur.status = MULT;
                    }
                    break;
                case LET:
                    if (expression[start] == ')') { // let 表达式的最后一个 expr 表达式
                        cur.value = calculateToken(token);
                        cur.status = LET2;
                    } else {
                        cur.var = token;
                        vars.back().push_back(token); // 记录该层作用域的所有变量, 方便后续的清除
                        cur.status = LET1;
                    }
                    break;
                case LET1:
                    scope[cur.var].push_back(calculateToken(token));
                    cur.status = LET;
                    break;
                case ADD:
                    cur.e1 = calculateToken(token);
                    cur.status = ADD1;
                    break;
                case ADD1:
                    cur.e2 = calculateToken(token);
                    cur.status = ADD2;
                    break;
                case MULT:
                    cur.e1 = calculateToken(token);
                    cur.status = MULT1;
                    break;
                case MULT1:
                    cur.e2 = calculateToken(token);
                    cur.status = MULT2;
                    break;
            }
        }
        return cur.value;
    }

    int calculateToken(const string &token) {
        if (islower(token[0])) {
            return scope[token].back();
        } else {
            return stoi(token);
        }
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
class Solution {
    Map<String, Deque<Integer>> scope = new HashMap<String, Deque<Integer>>();

    public int evaluate(String expression) {
        Deque<Deque<String>> vars = new ArrayDeque<Deque<String>>();
        int start = 0, n = expression.length();
        Deque<Expr> stack = new ArrayDeque<Expr>();
        Expr cur = new Expr(ExprStatus.VALUE);
        while (start < n) {
            if (expression.charAt(start) == ' ') {
                start++; // 去掉空格
                continue;
            }
            if (expression.charAt(start) == '(') {
                start++; // 去掉左括号
                stack.push(cur);
                cur = new Expr(ExprStatus.NONE);
                continue;
            }
            StringBuffer sb = new StringBuffer();
            if (expression.charAt(start) == ')') { // 本质上是把表达式转成一个 token
                start++; // 去掉右括号
                if (cur.status == ExprStatus.LET2) {
                    sb = new StringBuffer(Integer.toString(cur.value));
                    for (String var : vars.peek()) { // 清除作用域
                        scope.get(var).pop();
                    }
                    vars.pop();
                } else if (cur.status == ExprStatus.ADD2) {
                    sb = new StringBuffer(Integer.toString(cur.e1 + cur.e2));
                } else {
                    sb = new StringBuffer(Integer.toString(cur.e1 * cur.e2));
                }
                cur = stack.pop(); // 获取上层状态
            } else {
                while (start < n && expression.charAt(start) != ' ' && expression.charAt(start) != ')') {
                    sb.append(expression.charAt(start));
                    start++;
                }
            }
            String token = sb.toString();
            switch (cur.status.toString()) {
            case "VALUE":
                cur.value = Integer.parseInt(token);
                cur.status = ExprStatus.DONE;
                break;
            case "NONE":
                if ("let".equals(token)) {
                    cur.status = ExprStatus.LET;
                    vars.push(new ArrayDeque<String>()); // 记录该层作用域的所有变量, 方便后续的清除
                } else if ("add".equals(token)) {
                    cur.status = ExprStatus.ADD;
                } else if ("mult".equals(token)) {
                    cur.status = ExprStatus.MULT;
                }
                break;
            case "LET":
                if (expression.charAt(start) == ')') { // let 表达式的最后一个 expr 表达式
                    cur.value = calculateToken(token);
                    cur.status = ExprStatus.LET2;
                } else {
                    cur.var = token;
                    vars.peek().push(token); // 记录该层作用域的所有变量, 方便后续的清除
                    cur.status = ExprStatus.LET1;
                }
                break;
            case "LET1":
                scope.putIfAbsent(cur.var, new ArrayDeque<Integer>());
                scope.get(cur.var).push(calculateToken(token));
                cur.status = ExprStatus.LET;
                break;
            case "ADD":
                cur.e1 = calculateToken(token);
                cur.status = ExprStatus.ADD1;
                break;
            case "ADD1":
                cur.e2 = calculateToken(token);
                cur.status = ExprStatus.ADD2;
                break;
            case "MULT":
                cur.e1 = calculateToken(token);
                cur.status = ExprStatus.MULT1;
                break;
            case "MULT1":
                cur.e2 = calculateToken(token);
                cur.status = ExprStatus.MULT2;
                break;
            }
        }
        return cur.value;
    }

    public int calculateToken(String token) {
        if (Character.isLowerCase(token.charAt(0))) {
            return scope.get(token).peek();
        } else {
            return Integer.parseInt(token);
        }
    }
}

enum ExprStatus {
    VALUE,     // 初始状态
    NONE,      // 表达式类型未知
    LET,       // let 表达式
    LET1,      // let 表达式已经解析了 vi 变量
    LET2,      // let 表达式已经解析了最后一个表达式 expr
    ADD,       // add 表达式
    ADD1,      // add 表达式已经解析了 e1 表达式
    ADD2,      // add 表达式已经解析了 e2 表达式
    MULT,      // mult 表达式
    MULT1,     // mult 表达式已经解析了 e1 表达式
    MULT2,     // mult 表达式已经解析了 e2 表达式
    DONE       // 解析完成
}

class Expr {
    ExprStatus status;
    String var; // let 的变量 vi
    int value; // VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
    int e1, e2; // add 或 mult 表达式的两个表达式 e1 和 e2 的数值

    public Expr(ExprStatus s) {
        status = s;
    }
}
[sol2-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
public class Solution {
    Dictionary<string, Stack<int>> scope = new Dictionary<string, Stack<int>>();

    public int Evaluate(string expression) {
        Stack<Stack<string>> vars = new Stack<Stack<string>>();
        int start = 0, n = expression.Length;
        Stack<Expr> stack = new Stack<Expr>();
        Expr cur = new Expr(ExprStatus.VALUE);
        while (start < n) {
            if (expression[start] == ' ') {
                start++; // 去掉空格
                continue;
            }
            if (expression[start] == '(') {
                start++; // 去掉左括号
                stack.Push(cur);
                cur = new Expr(ExprStatus.NONE);
                continue;
            }
            StringBuilder sb = new StringBuilder();
            if (expression[start] == ')') { // 本质上是把表达式转成一个 token
                start++; // 去掉右括号
                if (cur.status == ExprStatus.LET2) {
                    sb = new StringBuilder(cur.value.ToString());
                    foreach (string var in vars.Peek()) { // 清除作用域
                        scope[var].Pop();
                    }
                    vars.Pop();
                } else if (cur.status == ExprStatus.ADD2) {
                    sb = new StringBuilder((cur.e1 + cur.e2).ToString());
                } else {
                    sb = new StringBuilder((cur.e1 * cur.e2).ToString());
                }
                cur = stack.Pop(); // 获取上层状态
            } else {
                while (start < n && expression[start] != ' ' && expression[start] != ')') {
                    sb.Append(expression[start]);
                    start++;
                }
            }
            string token = sb.ToString();
            switch (cur.status.ToString()) {
            case "VALUE":
                cur.value = int.Parse(token);
                cur.status = ExprStatus.DONE;
                break;
            case "NONE":
                if ("let".Equals(token)) {
                    cur.status = ExprStatus.LET;
                    vars.Push(new Stack<string>()); // 记录该层作用域的所有变量, 方便后续的清除
                } else if ("add".Equals(token)) {
                    cur.status = ExprStatus.ADD;
                } else if ("mult".Equals(token)) {
                    cur.status = ExprStatus.MULT;
                }
                break;
            case "LET":
                if (expression[start] == ')') { // let 表达式的最后一个 expr 表达式
                    cur.value = CalculateToken(token);
                    cur.status = ExprStatus.LET2;
                } else {
                    cur.var = token;
                    vars.Peek().Push(token); // 记录该层作用域的所有变量, 方便后续的清除
                    cur.status = ExprStatus.LET1;
                }
                break;
            case "LET1":
                if (!scope.ContainsKey(cur.var)) {
                    scope.Add(cur.var, new Stack<int>());
                }
                scope[cur.var].Push(CalculateToken(token));
                cur.status = ExprStatus.LET;
                break;
            case "ADD":
                cur.e1 = CalculateToken(token);
                cur.status = ExprStatus.ADD1;
                break;
            case "ADD1":
                cur.e2 = CalculateToken(token);
                cur.status = ExprStatus.ADD2;
                break;
            case "MULT":
                cur.e1 = CalculateToken(token);
                cur.status = ExprStatus.MULT1;
                break;
            case "MULT1":
                cur.e2 = CalculateToken(token);
                cur.status = ExprStatus.MULT2;
                break;
            }
        }
        return cur.value;
    }

    public int CalculateToken(string token) {
        if (char.IsLower(token[0])) {
            return scope[token].Peek();
        } else {
            return int.Parse(token);
        }
    }
}

public enum ExprStatus {
    VALUE,     // 初始状态
    NONE,      // 表达式类型未知
    LET,       // let 表达式
    LET1,      // let 表达式已经解析了 vi 变量
    LET2,      // let 表达式已经解析了最后一个表达式 expr
    ADD,       // add 表达式
    ADD1,      // add 表达式已经解析了 e1 表达式
    ADD2,      // add 表达式已经解析了 e2 表达式
    MULT,      // mult 表达式
    MULT1,     // mult 表达式已经解析了 e1 表达式
    MULT2,     // mult 表达式已经解析了 e2 表达式
    DONE       // 解析完成
}

public class Expr {
    public ExprStatus status;
    public string var; // let 的变量 vi
    public int value; // VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
    public int e1, e2; // add 或 mult 表达式的两个表达式 e1 和 e2 的数值

    public Expr(ExprStatus s) {
        status = s;
    }
}
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
#define MAX_VAR_LEN 64
#define MAX_VAR_SIZE 1024

typedef struct {
    char key[MAX_VAR_LEN];
    struct ListNode *lst;
    UT_hash_handle hh;
} HashItem;

typedef struct VarNode {
    char *var[MAX_VAR_SIZE];
    int varSize;
    struct VarNode *next;
} VarNode;

HashItem *scope = NULL;

typedef enum ExprStatus {
    VALUE = 0, // 初始状态
    NONE,      // 表达式类型未知
    LET,       // let 表达式
    LET1,      // let 表达式已经解析了 vi 变量
    LET2,      // let 表达式已经解析了最后一个表达式 expr
    ADD,       // add 表达式
    ADD1,      // add 表达式已经解析了 e1 表达式
    ADD2,      // add 表达式已经解析了 e2 表达式
    MULT,      // mult 表达式
    MULT1,     // mult 表达式已经解析了 e1 表达式
    MULT2,     // mult 表达式已经解析了 e2 表达式
    DONE       // 解析完成
} ExprStatus;

typedef struct Expr {
    ExprStatus status;
    char var[MAX_VAR_LEN]; // let 的变量 vi
    int value; // VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
    int e1, e2; // add 或 mult 表达式的两个表达式 e1 和 e2 的数值
} Expr;

Expr *creatExpr(ExprStatus s) {
    Expr *e = (Expr *)malloc(sizeof(Expr));
    e->status = s;
    e->value = 0;
    return e;
}

VarNode *creatVarNode() {
    VarNode *node = (VarNode *)malloc(sizeof(VarNode));
    node->varSize = 0;
    node->next = NULL;
    return node;
}

int calculateToken(const char *token) {
    if (islower(token[0])) {
        HashItem *pEntry = NULL;
        HASH_FIND_STR(scope, token, pEntry);
        return pEntry->lst->val;
    } else {
        return atoi(token);
    }
}

void freeScope() {
    HashItem *curr, *tmp;
    HASH_ITER(hh, scope, curr, tmp) {
      HASH_DEL(scope, curr);
      for (struct ListNode *node = curr->lst; node; ) {
          struct ListNode *pNode = node;
          node = node->next;
          free(pNode);
      }
      free(curr);
    }
}

int evaluate(char * expression){
    VarNode *vars = NULL;
    int start = 0, n = strlen(expression);
    Expr **st = (Expr **)malloc(sizeof(Expr *) * n);
    int top = 0;
    Expr *cur = creatExpr(VALUE);
    HashItem *pEntry = NULL;
    while (start < n) {
        if (expression[start] == ' ') {
            start++; // 去掉空格
            continue;
        }
        if (expression[start] == '(') {
            start++; // 去掉左括号
            st[top++] = cur;
            cur = creatExpr(NONE);
            continue;
        }
        char token[MAX_VAR_LEN];
        int pos = 0;
        if (expression[start] == ')') { // 本质上是把表达式转成一个 token
            start++; // 去掉右括号
            if (cur->status == LET2) {
                pos = sprintf(token, "%d", cur->value);
                for (int i = 0; i < vars->varSize; i++) {
                    pEntry = NULL;
                    HASH_FIND_STR(scope, vars->var[i], pEntry);
                    if (pEntry) {
                        struct ListNode *pNode = pEntry->lst; // 清除当前作用域的变量
                        if (pEntry->lst) {
                            pEntry->lst = pEntry->lst->next;
                            free(pNode);
                        }
                    }
                    free(vars->var[i]);
                }
                VarNode *prev = vars;
                vars = vars->next;    
                free(prev);        
            } else if (cur->status == ADD2) {
                pos = sprintf(token, "%d", cur->e1 + cur->e2);
            } else {
                pos = sprintf(token, "%d", cur->e1 * cur->e2);
            }
            free(cur);
            cur = st[top - 1]; // 获取上层状态
            top--;
        } else {
            while (start < n && expression[start] != ' ' && expression[start] != ')') {
                token[pos++] = expression[start];
                token[pos] = '\0';
                start++;
            }
        }
        switch (cur->status) {
            case VALUE:
                cur->value = atoi(token);
                cur->status = DONE;
                break;
            case NONE:
                if (!strcmp(token, "let")) {
                    cur->status = LET;
                    VarNode *pNode = creatVarNode();
                    pNode->next = vars;
                    vars = pNode; // 记录该层作用域的所有变量, 方便后续的清除
                } else if (!strcmp(token, "add")) {
                    cur->status = ADD;
                } else if (!strcmp(token, "mult")) {
                    cur->status = MULT;
                }
                break;
            case LET:
                if (expression[start] == ')') { // let 表达式的最后一个 expr 表达式
                    cur->value = calculateToken(token);
                    cur->status = LET2;
                } else {
                    strcpy(cur->var, token);
                    vars->var[vars->varSize] = (char *)malloc(sizeof(char) * (strlen(token) + 1));
                    strcpy(vars->var[vars->varSize++], token); // 记录该层作用域的所有变量, 方便后续的清除      
                    cur->status = LET1;         
                }
                break;
            case LET1:
                pEntry = NULL;
                HASH_FIND_STR(scope, cur->var, pEntry);
                if (NULL == pEntry) {
                    pEntry = (HashItem *)malloc(sizeof(HashItem));
                    strcpy(pEntry->key, cur->var);
                    pEntry->lst = NULL;
                    HASH_ADD_STR(scope, key, pEntry);
                }
                struct ListNode *pNode = (struct ListNode *)malloc(sizeof(struct ListNode));
                pNode->val = calculateToken(token);
                pNode->next = pEntry->lst;
                pEntry->lst = pNode; 
                cur->status = LET;
                break;
            case ADD:
                cur->e1 = calculateToken(token);
                cur->status = ADD1;
                break;
            case ADD1:
                cur->e2 = calculateToken(token);
                cur->status = ADD2;
                break;
            case MULT:
                cur->e1 = calculateToken(token);
                cur->status = MULT1;
                break;
            case MULT1:
                cur->e2 = calculateToken(token);
                cur->status = MULT2;
                break;
        }
    }
    freeScope();
    return cur->value;
}
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
const (
    VALUE = iota // 初始状态
    NONE         // 表达式类型未知
    LET          // let 表达式
    LET1         // let 表达式已经解析了 vi 变量
    LET2         // let 表达式已经解析了最后一个表达式 expr
    ADD          // add 表达式
    ADD1         // add 表达式已经解析了 e1 表达式
    ADD2         // add 表达式已经解析了 e2 表达式
    MULT         // mult 表达式
    MULT1        // mult 表达式已经解析了 e1 表达式
    MULT2        // mult 表达式已经解析了 e2 表达式
    DONE         // 解析完成
)

type expr struct {
    status int
    vr     string // let 的变量 vi
    value  int    // VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
    e1, e2 int    // add 或 mult 表达式的两个表达式 e1 和 e2 的数值
}

func evaluate(expression string) int {
    scope := map[string][]int{}
    calculateToken := func(token string) int {
        if unicode.IsLower(rune(token[0])) {
            vals := scope[token]
            return vals[len(vals)-1]
        }
        val, _ := strconv.Atoi(token)
        return val
    }

    vars := [][]string{}
    s := []expr{}
    cur := expr{status: VALUE}
    for i, n := 0, len(expression); i < n; {
        if expression[i] == ' ' {
            i++ // 去掉空格
            continue
        }
        if expression[i] == '(' {
            i++ // 去掉左括号
            s = append(s, cur)
            cur.status = NONE
            continue
        }
        var token string
        if expression[i] == ')' { // 本质上是把表达式转成一个 token
            i++ // 去掉右括号
            if cur.status == LET2 {
                token = strconv.Itoa(cur.value)
                for _, vr := range vars[len(vars)-1] { // 清除作用域
                    scope[vr] = scope[vr][:len(scope[vr])-1]
                }
                vars = vars[:len(vars)-1]
            } else if cur.status == ADD2 {
                token = strconv.Itoa(cur.e1 + cur.e2)
            } else {
                token = strconv.Itoa(cur.e1 * cur.e2)
            }
            cur, s = s[len(s)-1], s[:len(s)-1] // 获取上层状态
        } else {
            i0 := i
            for i < n && expression[i] != ' ' && expression[i] != ')' {
                i++
            }
            token = expression[i0:i]
        }

        switch cur.status {
        case VALUE:
            cur.value, _ = strconv.Atoi(token)
            cur.status = DONE
        case NONE:
            if token == "let" {
                cur.status = LET
                vars = append(vars, nil) // 记录该层作用域的所有变量, 方便后续的清除
            } else if token == "add" {
                cur.status = ADD
            } else if token == "mult" {
                cur.status = MULT
            }
        case LET:
            if expression[i] == ')' { // let 表达式的最后一个 expr 表达式
                cur.value = calculateToken(token)
                cur.status = LET2
            } else {
                cur.vr = token
                vars[len(vars)-1] = append(vars[len(vars)-1], token) // 记录该层作用域的所有变量, 方便后续的清除
                cur.status = LET1
            }
        case LET1:
            scope[cur.vr] = append(scope[cur.vr], calculateToken(token))
            cur.status = LET
        case ADD:
            cur.e1 = calculateToken(token)
            cur.status = ADD1
        case ADD1:
            cur.e2 = calculateToken(token)
            cur.status = ADD2
        case MULT:
            cur.e1 = calculateToken(token)
            cur.status = MULT1
        case MULT1:
            cur.e2 = calculateToken(token)
            cur.status = MULT2
        }
    }
    return cur.value
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
var evaluate = function(expression) {
    const scope = new Map();
    let vars = [];
    let start = 0, n = expression.length;
    const stack = [];
    let cur = new Expr(ExprStatus.VALUE);

    while (start < n) {
        if (expression[start] === ' ') {
            start++; // 去掉空格
            continue;
        }
        if (expression[start] === '(') {
            start++; // 去掉左括号
            stack.push(cur);
            cur = new Expr(ExprStatus.NONE);
            continue;
        }
        let sb = '';
        if (expression[start] === ')') { // 本质上是把表达式转成一个 token
            start++; // 去掉右括号
            if (cur.status == ExprStatus.LET2) {
                sb = cur.value;
                for (const v of vars[vars.length - 1]) { // 清除作用域
                    scope.get(v).pop();
                }
                vars.pop();
            } else if (cur.status === ExprStatus.ADD2) {
                sb = cur.e1 + cur.e2;
            } else {
                sb = cur.e1 * cur.e2;
            }
            cur = stack.pop(); // 获取上层状态
        } else {
            while (start < n && expression[start] !== ' ' && expression[start] !== ')') {
                sb += expression[start];
                start++;
            }
        }
        let token = sb;
        switch (cur.status) {
        case "VALUE":
            cur.value = parseInt(token);
            cur.status = ExprStatus.DONE;
            break;
        case "NONE":
            if ("let" === token) {
                cur.status = ExprStatus.LET;
                vars.push([]); // 记录该层作用域的所有变量, 方便后续的清除
            } else if ("add" === token) {
                cur.status = ExprStatus.ADD;
            } else if ("mult" === token) {
                cur.status = ExprStatus.MULT;
            }
            break;
        case "LET":
            if (expression[start] === ')') { // let 表达式的最后一个 expr 表达式
                cur.value = calculateToken(scope, token);
                cur.status = ExprStatus.LET2;
            } else {
                cur.v = token;
                vars[vars.length - 1].push(token); // 记录该层作用域的所有变量, 方便后续的清除
                cur.status = ExprStatus.LET1;
            }
            break;
        case "LET1":
            if (!scope.has(cur.v)) {
                scope.set(cur.v, []);
            }
            scope.get(cur.v).push(calculateToken(scope, token));
            cur.status = ExprStatus.LET;
            break;
        case "ADD":
            cur.e1 = calculateToken(scope, token);
            cur.status = ExprStatus.ADD1;
            break;
        case "ADD1":
            cur.e2 = calculateToken(scope, token);
            cur.status = ExprStatus.ADD2;
            break;
        case "MULT":
            cur.e1 = calculateToken(scope, token);
            cur.status = ExprStatus.MULT1;
            break;
        case "MULT1":
            cur.e2 = calculateToken(scope, token);
            cur.status = ExprStatus.MULT2;
            break;
        }
    }
    return cur.value;
}

const calculateToken = (scope, token) => {
    if (token[0] >= 'a' && token[0] <= 'z') {
        const n = scope.get(token).length;
        return scope.get(token)[n - 1];
    } else {
        return parseInt(token);
    }
};

var ExprStatus = {
    VALUE: 'VALUE',     // 初始状态
    NONE: 'NONE',      // 表达式类型未知
    LET: 'LET',       // let 表达式
    LET1: 'LET1',      // let 表达式已经解析了 vi 变量
    LET2: 'LET2',      // let 表达式已经解析了最后一个表达式 expr
    ADD: 'ADD',       // add 表达式
    ADD1: 'ADD1',      // add 表达式已经解析了 e1 表达式
    ADD2: 'ADD2',      // add 表达式已经解析了 e2 表达式
    MULT: 'MULT',      // mult 表达式
    MULT1: 'MULT1',     // mult 表达式已经解析了 e1 表达式
    MULT2: 'MULT2',     // mult 表达式已经解析了 e2 表达式
    DONE: 'DONE'       // 解析完成
}

class Expr {
    constructor(s) {
        this.status = s;
        this.v = ''; // let 的变量 vi
        this.value = 0; // VALUE 状态的数值，或者 LET2 状态最后一个表达式的数值
        this.e1 = 0; // add 或 mult 表达式的两个表达式 e1 和 e2 的数值
        this.e2 = 0;
    }
}

复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 expression 的长度。状态机解析会遍历整个字符串，因此需要 O(n) 的时间。

  • 空间复杂度：O(n)。保存状态的栈以及作用域变量都需要 O(n) 的空间。

 Comments
On this page
0736-Lisp 语法解析