0764-最大加号标志

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

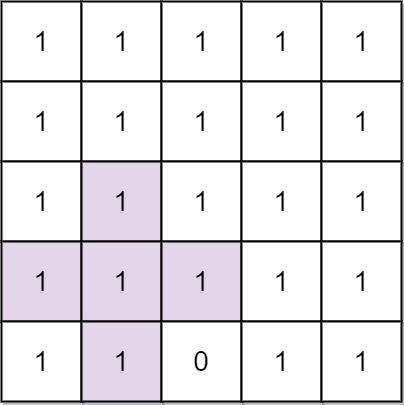
在一个 n x n 的矩阵 grid 中，除了在数组 mines 中给出的元素为 0，其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0

返回 _ _grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志，则返回 0 。

一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1
，以及4个从中心向上、向下、向左、向右延伸，长度为 k-1，由 1 组成的臂。注意，只有加号标志的所有网格要求为 1 ，别的网格可能为 0
也可能为 1 。

示例 1：

**输入:** n = 5, mines = [[4, 2]]
**输出:** 2
**解释:** 在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

示例 2：

**输入:** n = 1, mines = [[0, 0]]
**输出:** 0
**解释:** 没有加号标志，返回 0 。

提示：

  • 1 <= n <= 500
  • 1 <= mines.length <= 5000
  • 0 <= xi, yi < n
  • 每一对 (xi, yi) 都 不重复 ​​​​​​​

方法一：动态规划

思路与算法

对于每个中心点坐标 (i, j)，分别从上下左右四个方向计算从 (i, j) 开始最长连续 1 的个数。设 dp}[i][j][k] 表示以 (i, j) 为起点在方向 k 上的连续 1 的最大数目：

  • 如果 grid}[i][j] 为 0，那么此时该方向的连续 1 的最大数目为 0；
  • 如果 grid}[i][j] 为 1, 那么此时该方向的连续 1 的最大数目为该方向上前一个单元为起点的最大数目加 1；

假设当前 k = 0,1,2,3 时，分别表示方向为左、右、上、下，则我们可以得到递推公式如下：

\textit{dp}[i][j][0] =
\begin{cases}
0, & \textit{grid}[i][j] = 0 \
\textit{dp}[i][j-1][0] + 1 , & \textit{grid}[i][j] = 1 \
\end{cases}
\
\textit{dp}[i][j][1] =
\begin{cases}
0, & \textit{grid}[i][j] = 0 \
\textit{dp}[i][j+1][1] + 1 , & \textit{grid}[i][j] = 1 \
\end{cases}
\
\textit{dp}[i][j][2] =
\begin{cases}
0, & \textit{grid}[i][j] = 0 \
\textit{dp}[i-1][j][2] + 1 , & \textit{grid}[i][j] = 1 \
\end{cases}
\
\textit{dp}[i][j][3] =
\begin{cases}
0, & \textit{grid}[i][j] = 0 \
\textit{dp}[i+1][j][3] + 1 , & \textit{grid}[i][j] = 1 \
\end{cases}
\

假设网格中有一行为 01110110，当前方向为向左，那么对应的连续 1 的个数就是 012301201。以每个点为 (i,j) 为中心的四个方向中最小连续 1 的个数即为以其为中心构成的加号标志的最大阶数，我们用公式表示 L = \min\limits_{k=0}^{3}\textit{dp}[i][j][k]。在实际计算时，我们为了方便计算只用 dp}[i][j] 保存四个方向中最小的连续 1 的个数即可。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def orderOfLargestPlusSign(self, n: int, mines: List[List[int]]) -> int:
        dp = [[n] * n for _ in range(n)]
        banned = set(map(tuple, mines))
        for i in range(n):
            # left
            count = 0
            for j in range(n):
                count = 0 if (i, j) in banned else count + 1
                dp[i][j] = min(dp[i][j], count)
            # right
            count = 0
            for j in range(n - 1, -1, -1):
                count = 0 if (i, j) in banned else count + 1
                dp[i][j] = min(dp[i][j], count)
        for j in range(n):
            # up
            count = 0
            for i in range(n):
                count = 0 if (i, j) in banned else count + 1
                dp[i][j] = min(dp[i][j], count)
            # down
            count = 0
            for i in range(n - 1, -1, -1):
                count = 0 if (i, j) in banned else count + 1
                dp[i][j] = min(dp[i][j], count)
        return max(map(max, dp))
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class Solution {
public:
    int orderOfLargestPlusSign(int n, vector<vector<int>>& mines) {
        vector<vector<int>> dp(n, vector<int>(n, n));
        unordered_set<int> banned;
        for (auto &&vec : mines) {
            banned.emplace(vec[0] * n + vec[1]);
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int count = 0;
            /* left */
            for (int j = 0; j < n; j++) {
                if (banned.count(i * n + j)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[i][j] = min(dp[i][j], count);
            }
            count = 0;
            /* right */ 
            for (int j = n - 1; j >= 0; j--) {
                if (banned.count(i * n + j)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[i][j] = min(dp[i][j], count);
            }
        }
        for (int i = 0; i < n; i++) {
            int count = 0;
            /* up */
            for (int j = 0; j < n; j++) {
                if (banned.count(j * n + i)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[j][i] = min(dp[j][i], count);
            }
            count = 0;
            /* down */
            for (int j = n - 1; j >= 0; j--) {
                if (banned.count(j * n + i)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[j][i] = min(dp[j][i], count);
                ans = max(ans, dp[j][i]);
            }
        }
        return ans;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
    public int orderOfLargestPlusSign(int n, int[][] mines) {
        int[][] dp = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(dp[i], n);
        }
        Set<Integer> banned = new HashSet<Integer>();
        for (int[] vec : mines) {
            banned.add(vec[0] * n + vec[1]);
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int count = 0;
            /* left */
            for (int j = 0; j < n; j++) {
                if (banned.contains(i * n + j)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[i][j] = Math.min(dp[i][j], count);
            }
            count = 0;
            /* right */ 
            for (int j = n - 1; j >= 0; j--) {
                if (banned.contains(i * n + j)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[i][j] = Math.min(dp[i][j], count);
            }
        }
        for (int i = 0; i < n; i++) {
            int count = 0;
            /* up */
            for (int j = 0; j < n; j++) {
                if (banned.contains(j * n + i)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[j][i] = Math.min(dp[j][i], count);
            }
            count = 0;
            /* down */
            for (int j = n - 1; j >= 0; j--) {
                if (banned.contains(j * n + i)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[j][i] = Math.min(dp[j][i], count);
                ans = Math.max(ans, dp[j][i]);
            }
        }
        return ans;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class Solution {
    public int OrderOfLargestPlusSign(int n, int[][] mines) {
        int[][] dp = new int[n][];
        for (int i = 0; i < n; i++) {
            dp[i] = new int[n];
            Array.Fill(dp[i], n);
        }
        ISet<int> banned = new HashSet<int>();
        foreach (int[] vec in mines) {
            banned.Add(vec[0] * n + vec[1]);
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int count = 0;
            /* left */
            for (int j = 0; j < n; j++) {
                if (banned.Contains(i * n + j)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[i][j] = Math.Min(dp[i][j], count);
            }
            count = 0;
            /* right */ 
            for (int j = n - 1; j >= 0; j--) {
                if (banned.Contains(i * n + j)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[i][j] = Math.Min(dp[i][j], count);
            }
        }
        for (int i = 0; i < n; i++) {
            int count = 0;
            /* up */
            for (int j = 0; j < n; j++) {
                if (banned.Contains(j * n + i)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[j][i] = Math.Min(dp[j][i], count);
            }
            count = 0;
            /* down */
            for (int j = n - 1; j >= 0; j--) {
                if (banned.Contains(j * n + i)) {
                    count = 0;
                } else {
                    count++;
                }
                dp[j][i] = Math.Min(dp[j][i], count);
                ans = Math.Max(ans, dp[j][i]);
            }
        }
        return ans;
    }
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#define MAX(a, b) ((a) > (b) ? (a) : (b))
#define MIN(a, b) ((a) < (b) ? (a) : (b))

typedef struct {
    int key;
    UT_hash_handle hh;
} HashItem; 

HashItem *hashFindItem(HashItem **obj, int key) {
    HashItem *pEntry = NULL;
    HASH_FIND_INT(*obj, &key, pEntry);
    return pEntry;
}

bool hashAddItem(HashItem **obj, int key) {
    if (hashFindItem(obj, key)) {
        return false;
    }
    HashItem *pEntry = (HashItem *)malloc(sizeof(HashItem));
    pEntry->key = key;
    HASH_ADD_INT(*obj, key, pEntry);
    return true;
}

void hashFree(HashItem **obj) {
    HashItem *curr = NULL, *tmp = NULL;
    HASH_ITER(hh, *obj, curr, tmp) {
        HASH_DEL(*obj, curr);  
        free(curr);             
    }
}

int orderOfLargestPlusSign(int n, int** mines, int minesSize, int* minesColSize) {
    int dp[n][n];
    HashItem *banned = NULL;
    for (int i = 0; i < minesSize; i++) {
        hashAddItem(&banned, mines[i][0] * n + mines[i][1]);
    }
    int ans = 0;
    for (int i = 0; i < n; i++) {
        int count = 0;
        /* left */
        for (int j = 0; j < n; j++) {
            dp[i][j] = n;
            if (hashFindItem(&banned, i * n + j)) {
                count = 0;
            } else {
                count++;
            }
            dp[i][j] = MIN(dp[i][j], count);
        }
        count = 0;
        /* right */
        for (int j = n - 1; j >= 0; j--) {
            if (hashFindItem(&banned, i * n + j)) {
                count = 0;
            } else {
                count++;
            }
            dp[i][j] = MIN(dp[i][j], count);
        }
    }
    for (int i = 0; i < n; i++) {
        int count = 0;
        /* up */
        for (int j = 0; j < n; j++) {
            if (hashFindItem(&banned, j * n + i)) {
                count = 0;
            } else {
                count++;
            }
            dp[j][i] = MIN(dp[j][i], count);
        }
        count = 0;
        /* down */
        for (int j = n - 1; j >= 0; j--) {
            if (hashFindItem(&banned, j * n + i)) {
                count = 0;
            } else {
                count++;
            }
            dp[j][i] = MIN(dp[j][i], count);
            ans = MAX(ans, dp[j][i]);
        }
    }
    hashFree(&banned);
    return ans;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
func orderOfLargestPlusSign(n int, mines [][]int) (ans int) {
    dp := make([][]int, n)
    for i := range dp {
        dp[i] = make([]int, n)
        for j := range dp[i] {
            dp[i][j] = n
        }
    }
    banned := map[int]bool{}
    for _, p := range mines {
        banned[p[0]*n+p[1]] = true
    }
    for i := 0; i < n; i++ {
        count := 0
        /* left */
        for j := 0; j < n; j++ {
            if banned[i*n+j] {
                count = 0
            } else {
                count++
            }
            dp[i][j] = min(dp[i][j], count)
        }
        count = 0
        /* right */
        for j := n - 1; j >= 0; j-- {
            if banned[i*n+j] {
                count = 0
            } else {
                count++
            }
            dp[i][j] = min(dp[i][j], count)
        }
    }
    for i := 0; i < n; i++ {
        count := 0
        /* up */
        for j := 0; j < n; j++ {
            if banned[j*n+i] {
                count = 0
            } else {
                count++
            }
            dp[j][i] = min(dp[j][i], count)
        }
        count = 0
        /* down */
        for j := n - 1; j >= 0; j-- {
            if banned[j*n+i] {
                count = 0
            } else {
                count++
            }
            dp[j][i] = min(dp[j][i], count)
            ans = max(ans, dp[j][i])
        }
    }
    return ans
}

func min(a, b int) int {
    if a > b {
        return b
    }
    return a
}

func max(a, b int) int {
    if b > a {
        return b
    }
    return a
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
/**
 * @param {number} n
 * @param {number[][]} mines
 * @return {number}
 */
var orderOfLargestPlusSign = function(n, mines) {
    const dp = new Array(n).fill(0).map(() => new Array(n).fill(n));
    const banned = new Set();
    for (const vec of mines) {
        banned.add(vec[0] * n + vec[1]);
    }
    let ans = 0;
    for (let i = 0; i < n; i++) {
        let count = 0;
        /* left */
        for (let j = 0; j < n; j++) {
            if (banned.has(i * n + j)) {
                count = 0;
            } else {
                count++;
            }
            dp[i][j] = Math.min(dp[i][j], count);
        }
        count = 0;
        /* right */ 
        for (let j = n - 1; j >= 0; j--) {
            if (banned.has(i * n + j)) {
                count = 0;
            } else {
                count++;
            }
            dp[i][j] = Math.min(dp[i][j], count);
        }
    }
    for (let i = 0; i < n; i++) {
        let count = 0;
        /* up */
        for (let j = 0; j < n; j++) {
            if (banned.has(j * n + i)) {
                count = 0;
            } else {
                count++;
            }
            dp[j][i] = Math.min(dp[j][i], count);
        }
        count = 0;
        /* down */
        for (let j = n - 1; j >= 0; j--) {
            if (banned.has(j * n + i)) {
                count = 0;
            } else {
                count++;
            }
            dp[j][i] = Math.min(dp[j][i], count);
            ans = Math.max(ans, dp[j][i]);
        }
    }
    return ans;
};

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 表示矩阵的行数。我们最多需要遍历 4 次即可计算出每个点上的 4 方向上连续 1 的最大数目，因此需要的时间为 O(n^2)。

  • 空间复杂度：O(n^2)。我们需要保存每个点上的 4 方向上连续 1 的最小数目即可，需要的空间为 O(n^2)。

 Comments
On this page
0764-最大加号标志