给定一个字符串 s ,检查是否能重新排布其中的字母,使得两相邻的字符不同。
返回 s 的任意可能的重新排列。若不可行,返回空字符串 ""
示例 1:
**输入:** s = "aab"
**输出:** "aba"
示例 2:
**输入:** s = "aaab"
**输出:** ""
提示:
1 <= s.length <= 500s 只包含小写字母
前言 这道题是典型的使用贪心思想的题。重构字符串时,需要根据每个字母在字符串中出现的次数处理每个字母放置的位置。如果出现次数最多的字母可以在重新排布之后不相邻,则可以重新排布字母使得相邻的字母都不相同。如果出现次数最多的字母过多,则无法重新排布字母使得相邻的字母都不相同。
假设字符串的长度为 n,如果可以重新排布成相邻的字母都不相同的字符串,每个字母最多出现多少次?
当 n 是偶数时,有 \dfrac{n}{2 个偶数下标和 \dfrac{n}{2 个奇数下标,因此每个字母的出现次数都不能超过 \dfrac{n}{2 次,否则出现次数最多的字母一定会出现相邻。
当 n 是奇数时,由于共有 \dfrac{n+1/2 个偶数下标,因此每个字母的出现次数都不能超过 \dfrac{n+1/2 次,否则出现次数最多的字母一定会出现相邻。
由于当 n 是偶数时,\dfrac{n}{2} = \Big\lfloor \dfrac{n+1/2} \Big\rfloor,因此可以合并 n 是偶数与 n 是奇数的情况:如果可以重新排布成相邻的字母都不相同的字符串,每个字母最多出现 \Big\lfloor \dfrac{n+1/2} \Big\rfloor 次。
因此首先遍历字符串并统计每个字母的出现次数,如果存在一个字母的出现次数大于 \Big\lfloor \dfrac{n+1/2} \Big\rfloor,则无法重新排布字母使得相邻的字母都不相同,返回空字符串。如果所有字母的出现次数都不超过 \Big\lfloor \dfrac{n+1/2} \Big\rfloor,则考虑如何重新排布字母。
以下提供两种使用贪心的方法,分别基于最大堆和计数。
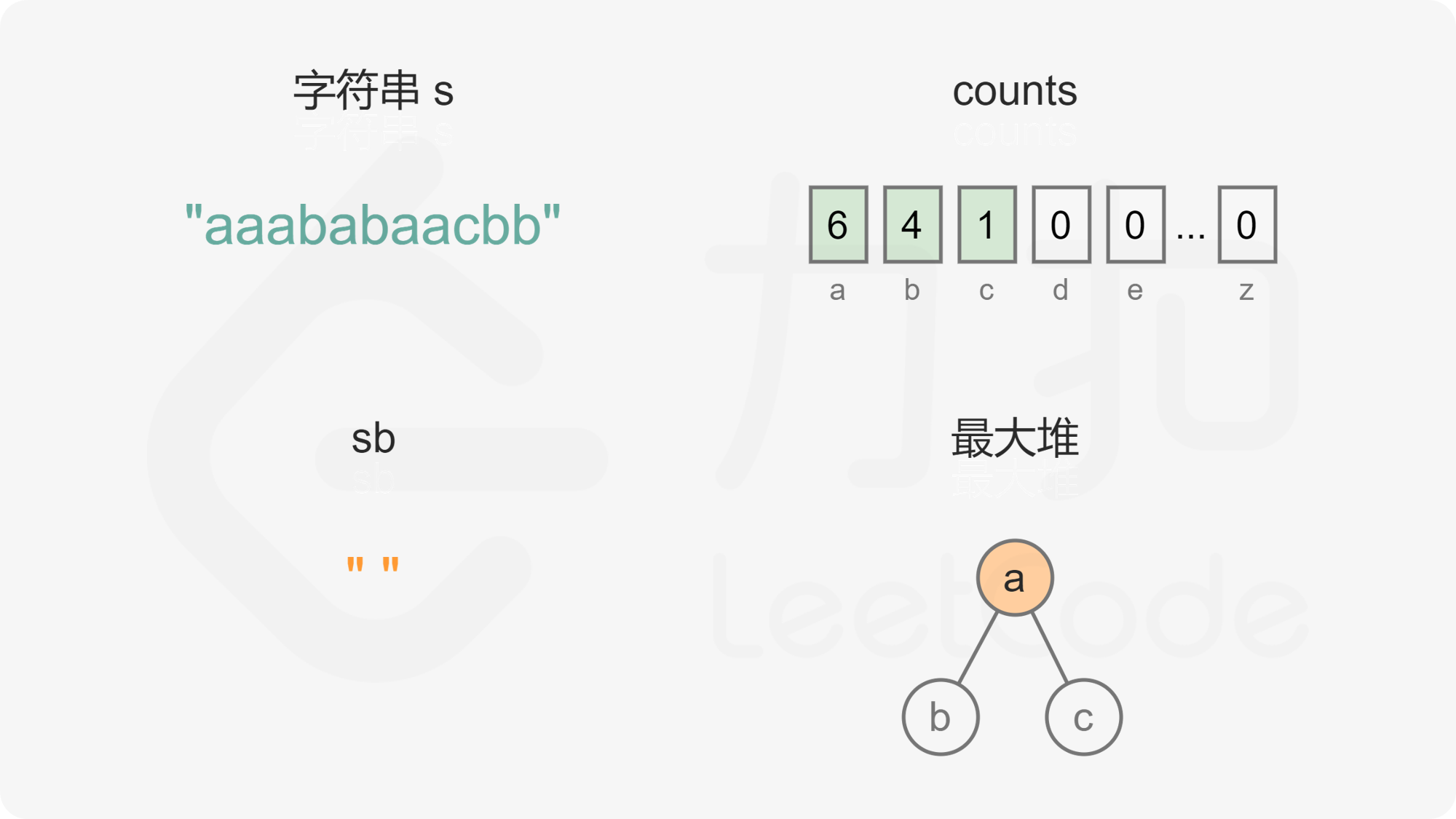
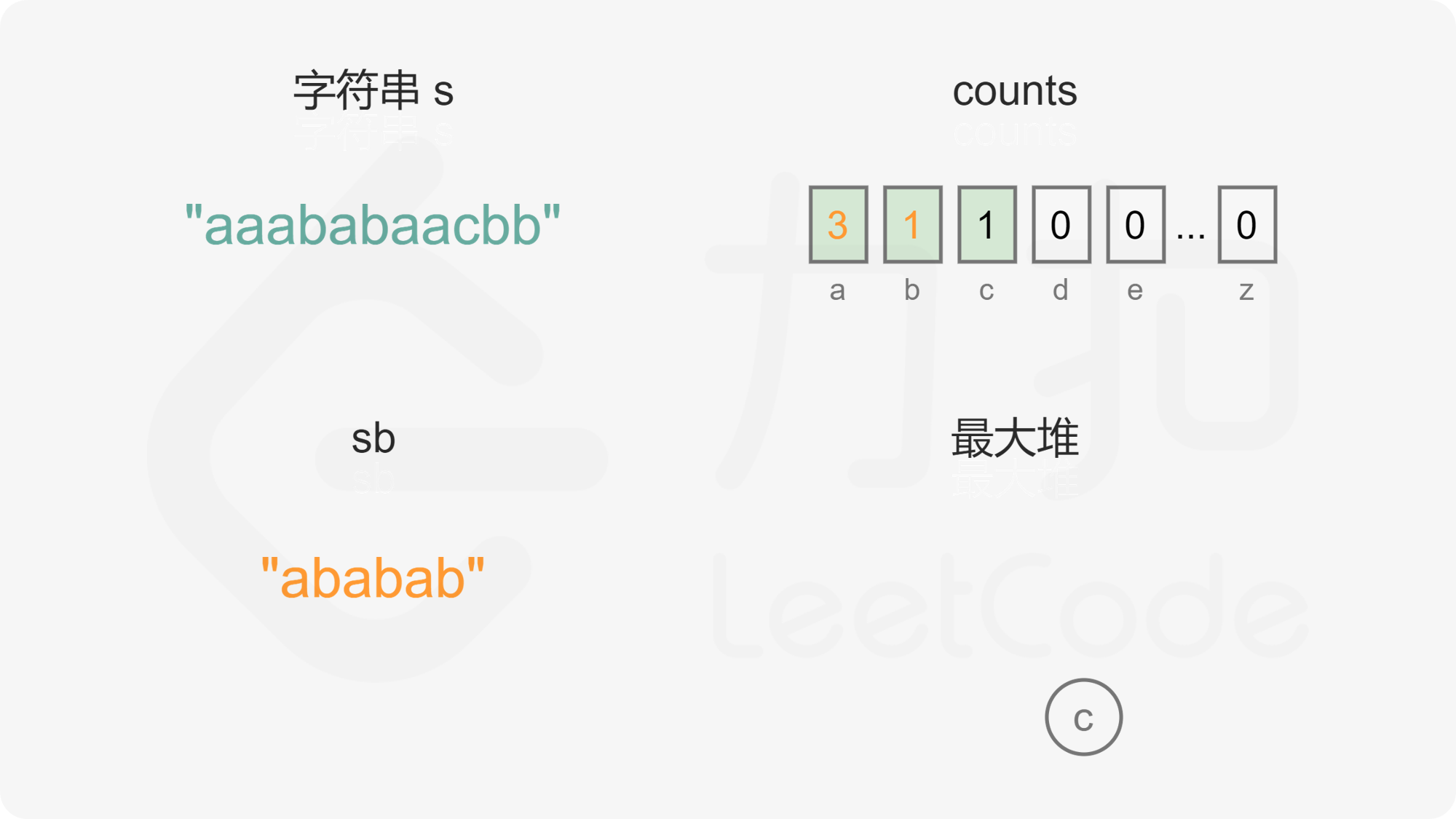
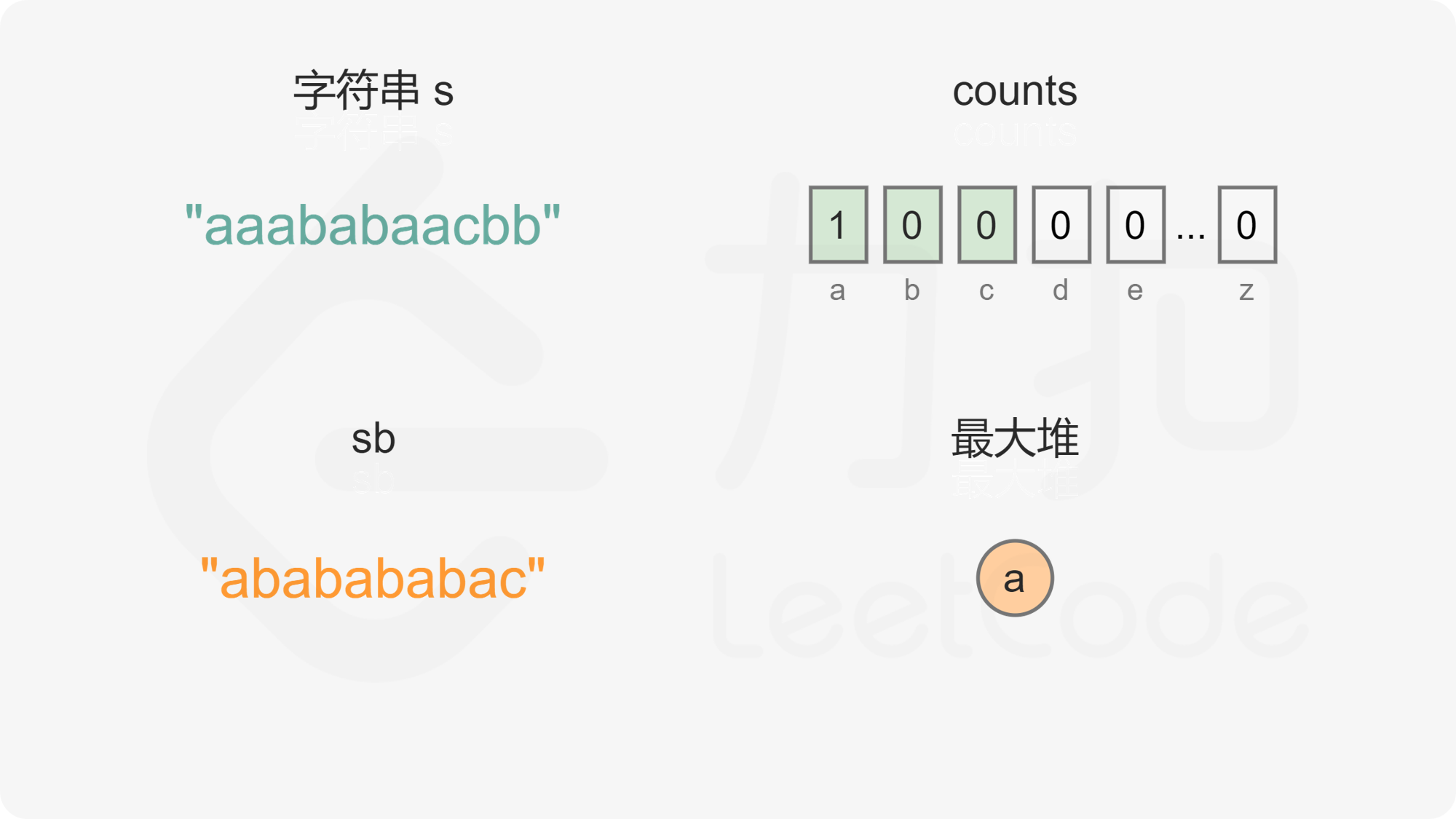
方法一:基于最大堆的贪心 维护最大堆存储字母,堆顶元素为出现次数最多的字母。首先统计每个字母的出现次数,然后将出现次数大于 0 的字母加入最大堆。
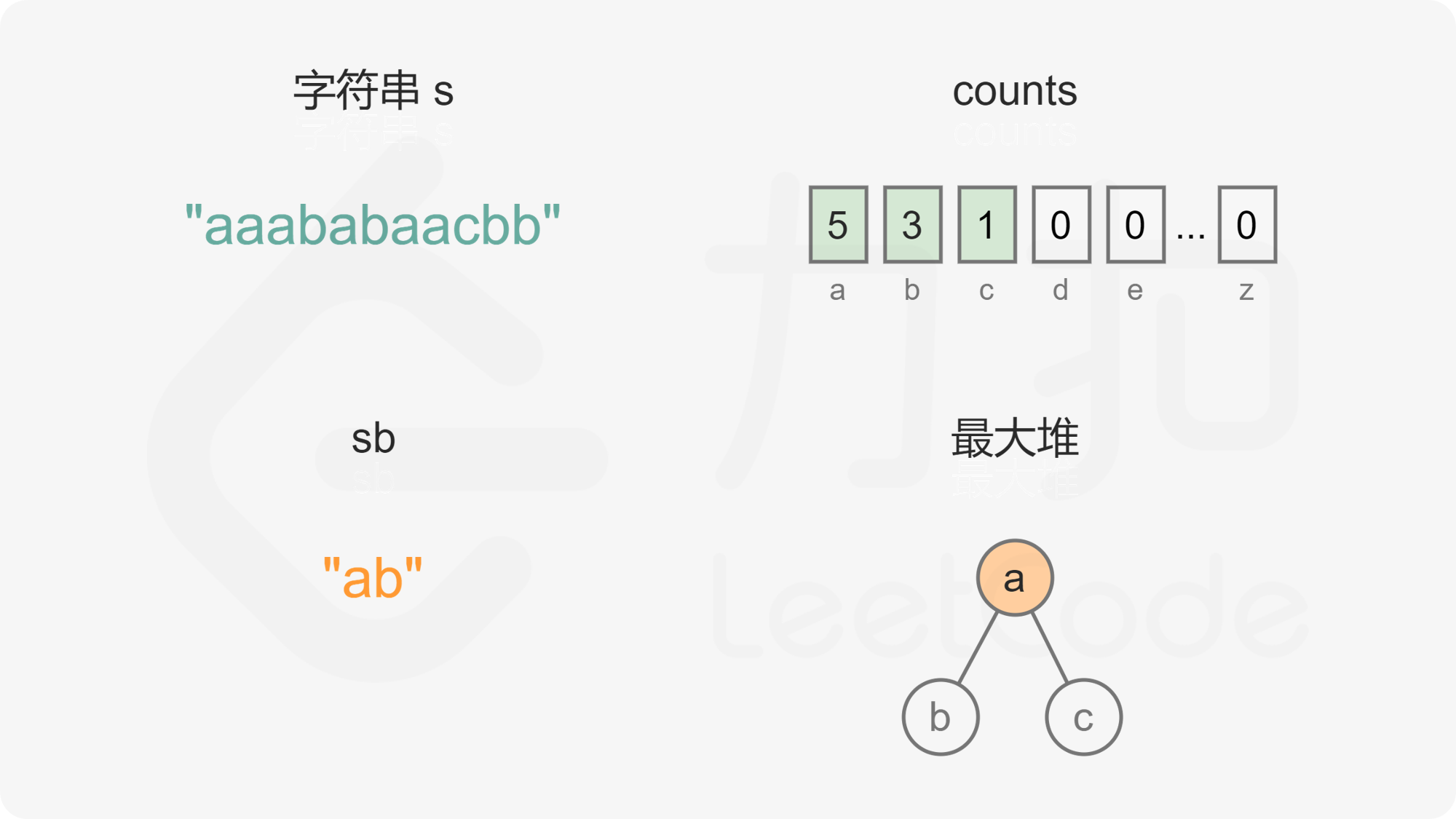
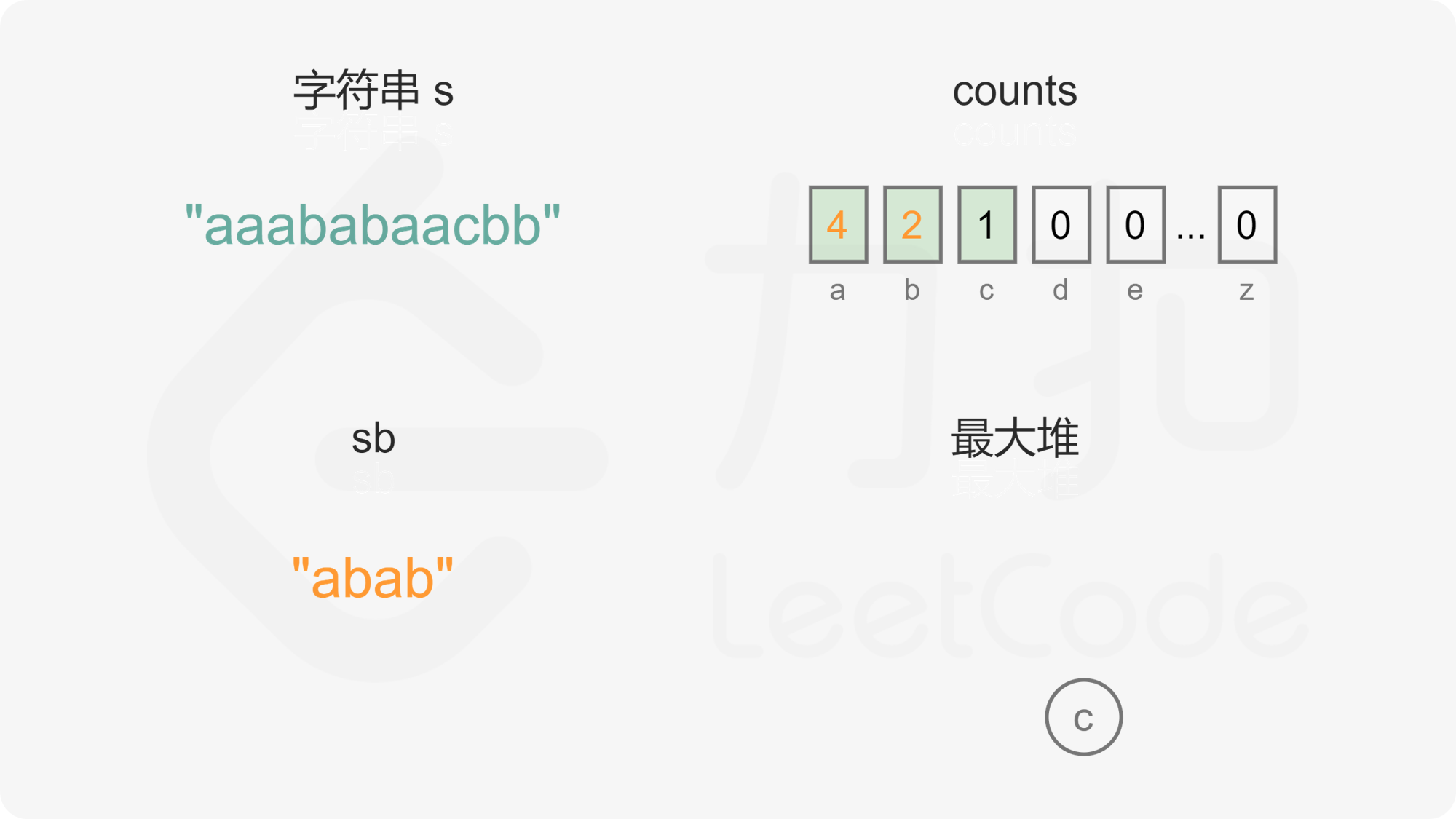
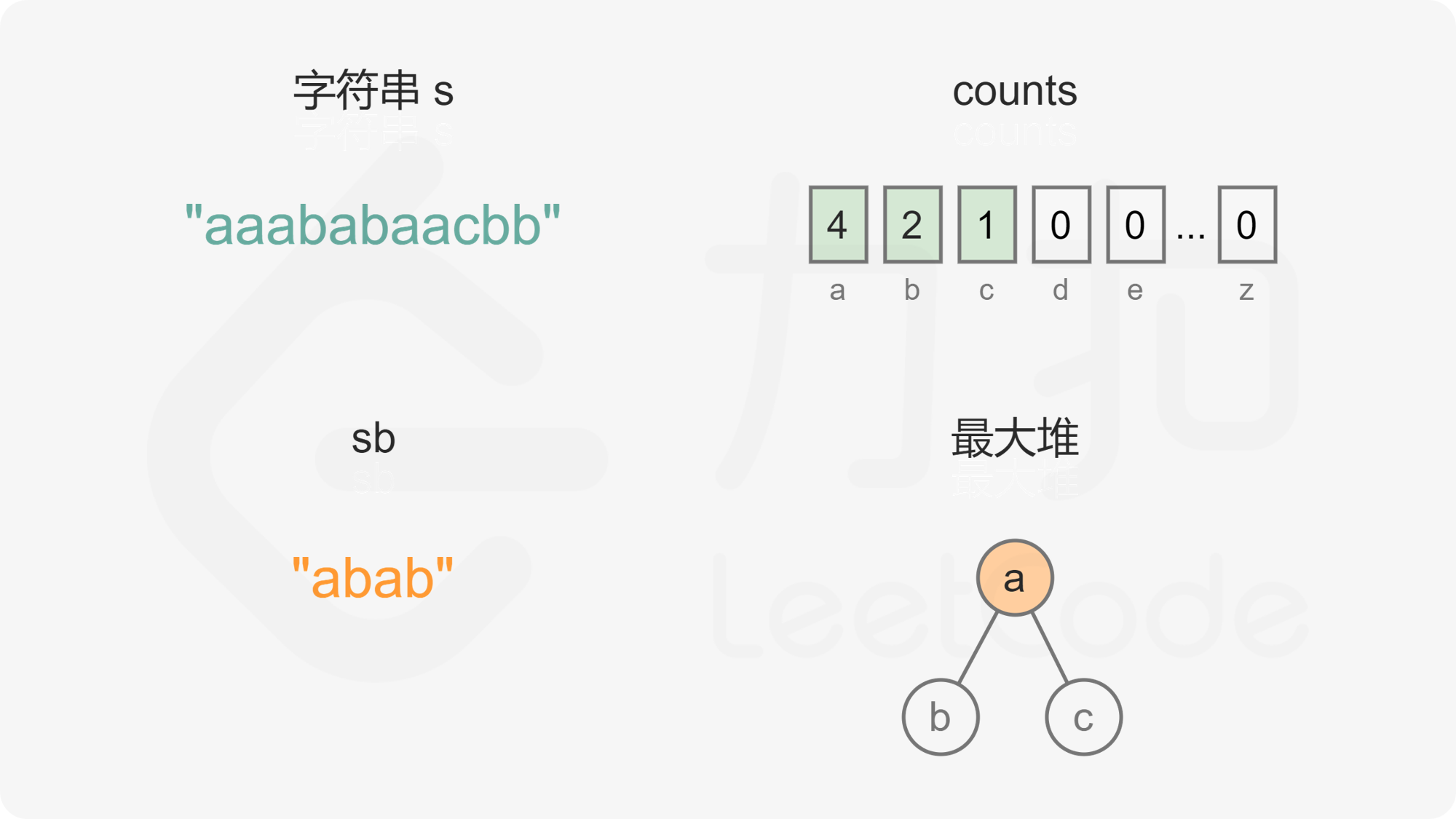
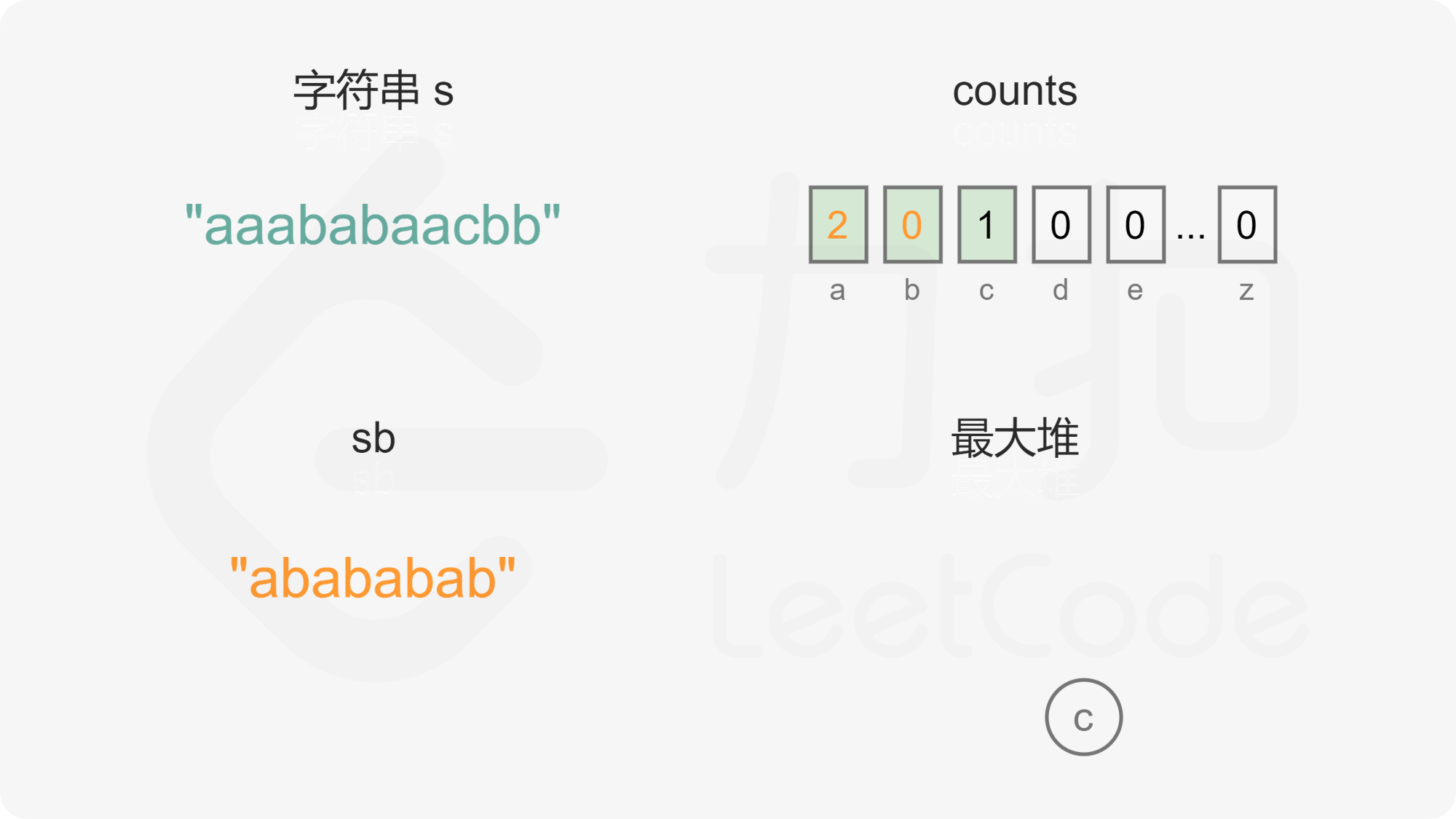
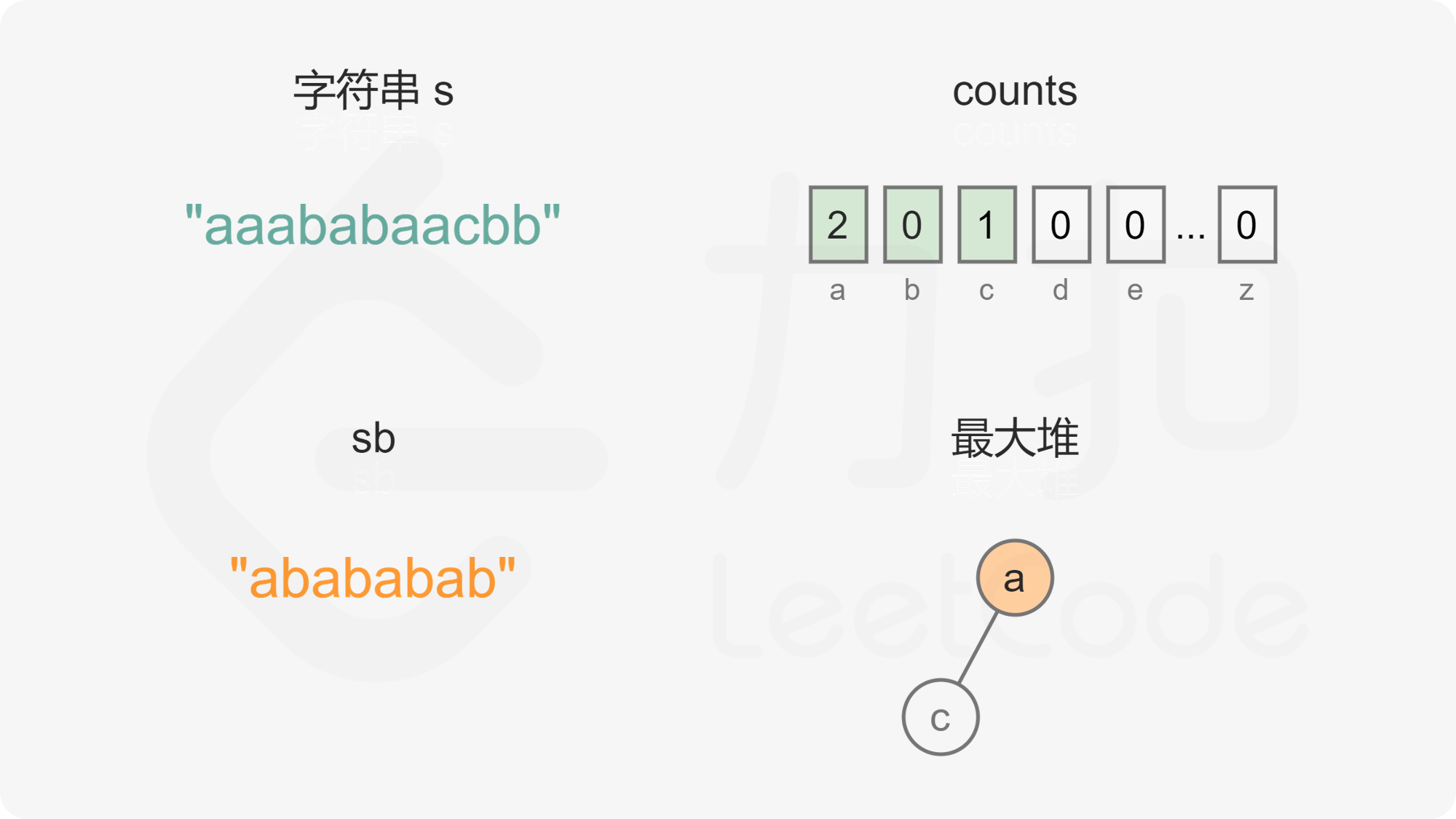
当最大堆的元素个数大于 1 时,每次从最大堆取出两个字母,拼接到重构的字符串,然后将两个字母的出现次数分别减 1,并将剩余出现次数大于 0 的字母重新加入最大堆。由于最大堆中的元素都是不同的,因此取出的两个字母一定也是不同的,将两个不同的字母拼接到重构的字符串,可以确保相邻的字母都不相同。
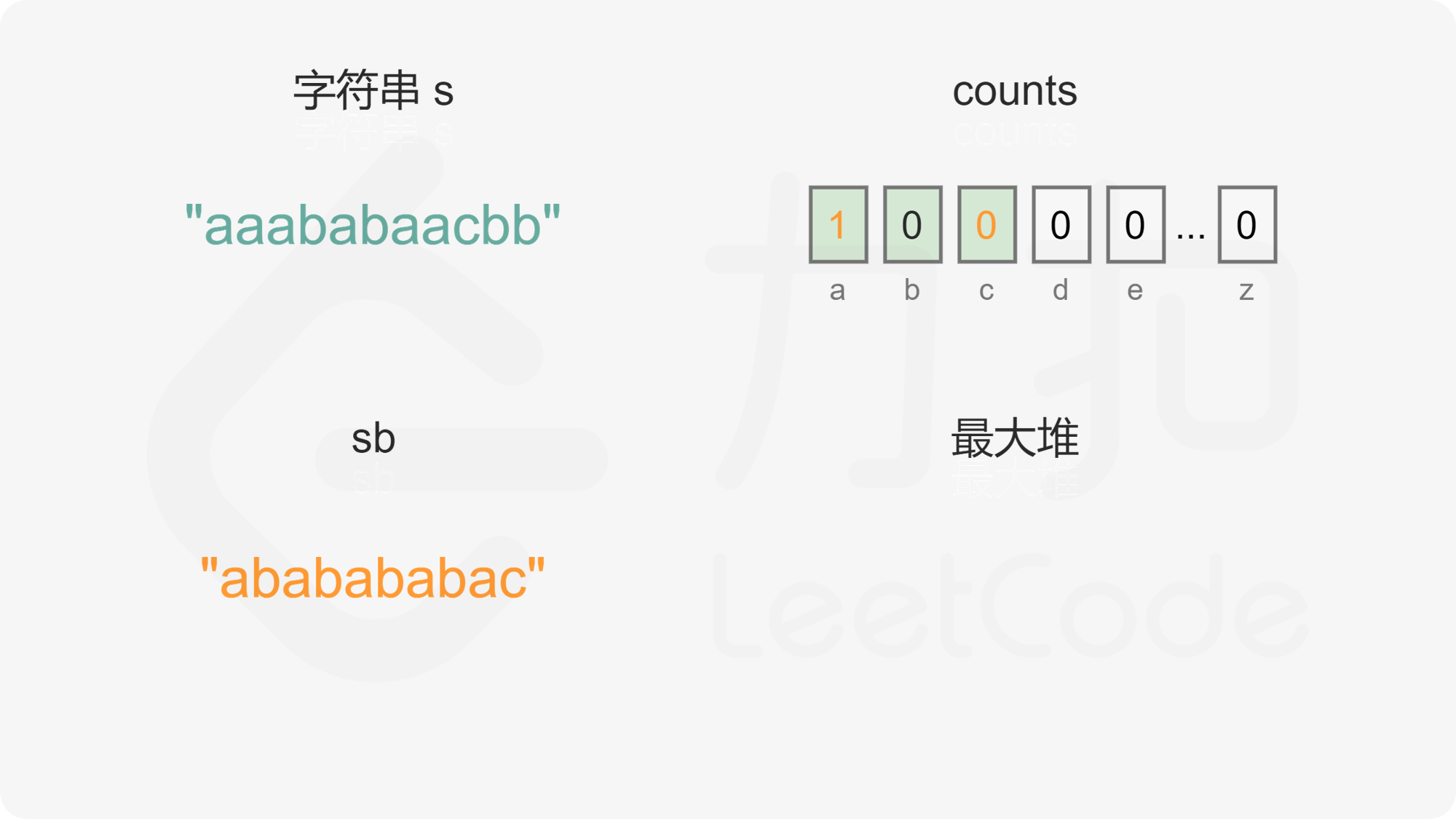
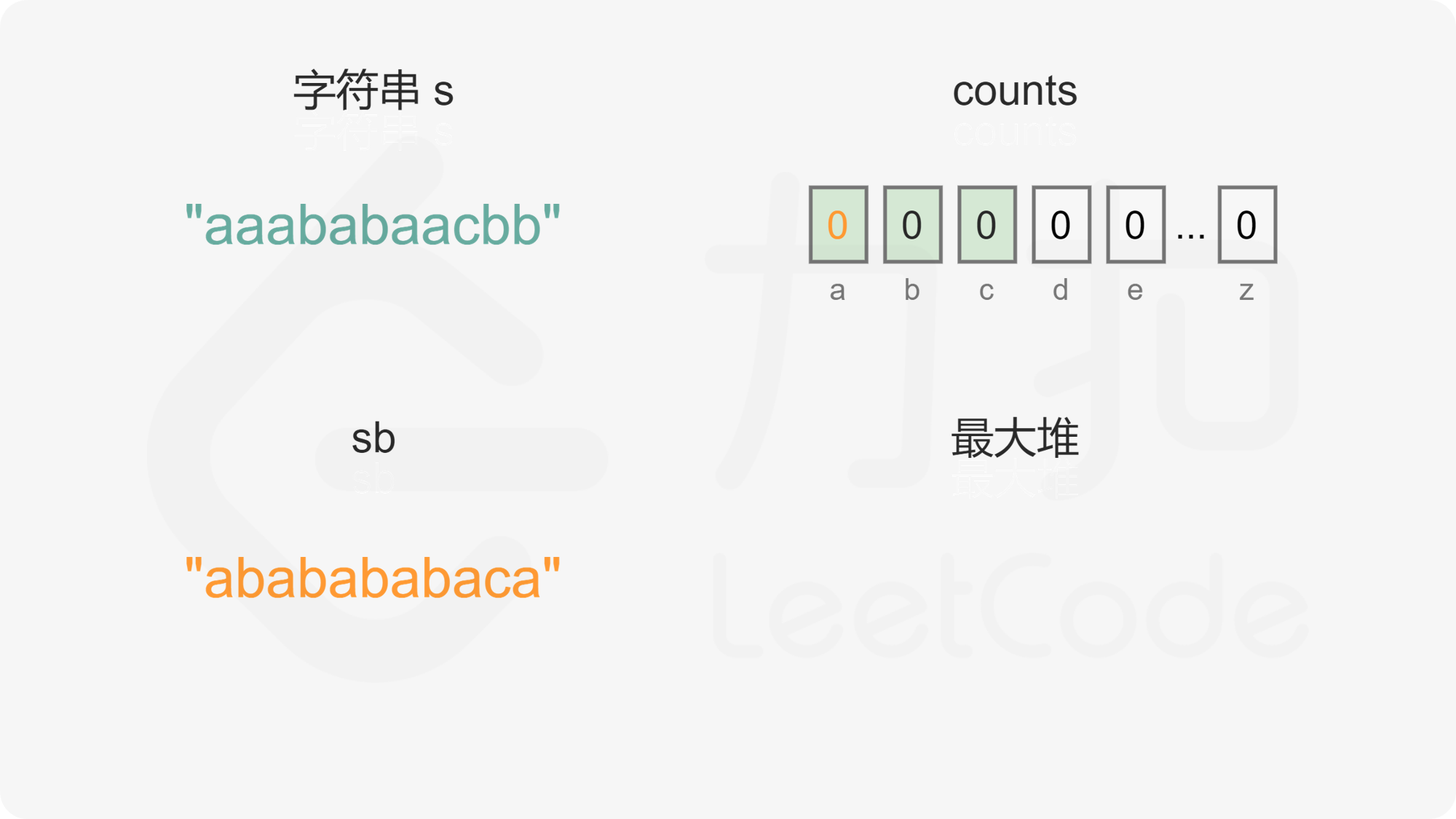
如果最大堆变成空,则已经完成字符串的重构。如果最大堆剩下 1 个元素,则取出最后一个字母,拼接到重构的字符串。
对于长度为 n 的字符串,共有 \Big\lfloor \dfrac{n}{2} \Big\rfloor 次每次从最大堆取出两个字母的操作,当 n 是奇数时,还有一次从最大堆取出一个字母的操作,因此重构的字符串的长度一定是 n。
当 n 是奇数时,是否可能出现重构的字符串的最后两个字母相同的情况?如果最后一个字母在整个字符串中至少出现了 2 次,则在最后一次从最大堆取出两个字母时,该字母会先被选出,因此不会成为重构的字符串的倒数第二个字母,也不可能出现重构的字符串最后两个字母相同的情况。
因此,在重构字符串可行的情况下,基于最大堆的贪心可以确保得到正确答案。
<
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class Solution { public String reorganizeString (String s) { if (s.length() < 2 ) { return s; } int [] counts = new int [26 ]; int maxCount = 0 ; int length = s.length(); for (int i = 0 ; i < length; i++) { char c = s.charAt(i); counts[c - 'a' ]++; maxCount = Math.max(maxCount, counts[c - 'a' ]); } if (maxCount > (length + 1 ) / 2 ) { return "" ; } PriorityQueue<Character> queue = new PriorityQueue <Character>(new Comparator <Character>() { public int compare (Character letter1, Character letter2) { return counts[letter2 - 'a' ] - counts[letter1 - 'a' ]; } }); for (char c = 'a' ; c <= 'z' ; c++) { if (counts[c - 'a' ] > 0 ) { queue.offer(c); } } StringBuffer sb = new StringBuffer (); while (queue.size() > 1 ) { char letter1 = queue.poll(); char letter2 = queue.poll(); sb.append(letter1); sb.append(letter2); int index1 = letter1 - 'a' , index2 = letter2 - 'a' ; counts[index1]--; counts[index2]--; if (counts[index1] > 0 ) { queue.offer(letter1); } if (counts[index2] > 0 ) { queue.offer(letter2); } } if (queue.size() > 0 ) { sb.append(queue.poll()); } return sb.toString(); } }
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 class Solution {public : string reorganizeString (string s) { if (s.length () < 2 ) { return s; } vector<int > counts (26 , 0 ) ; int maxCount = 0 ; int length = s.length (); for (int i = 0 ; i < length; i++) { char c = s[i]; counts[c - 'a' ]++; maxCount = max (maxCount, counts[c - 'a' ]); } if (maxCount > (length + 1 ) / 2 ) { return "" ; } auto cmp = [&](const char & letter1, const char & letter2) { return counts[letter1 - 'a' ] < counts[letter2 - 'a' ]; }; priority_queue<char , vector<char >, decltype (cmp)> queue{cmp}; for (char c = 'a' ; c <= 'z' ; c++) { if (counts[c - 'a' ] > 0 ) { queue.push (c); } } string sb = "" ; while (queue.size () > 1 ) { char letter1 = queue.top (); queue.pop (); char letter2 = queue.top (); queue.pop (); sb += letter1; sb += letter2; int index1 = letter1 - 'a' , index2 = letter2 - 'a' ; counts[index1]--; counts[index2]--; if (counts[index1] > 0 ) { queue.push (letter1); } if (counts[index2] > 0 ) { queue.push (letter2); } } if (queue.size () > 0 ) { sb += queue.top (); } return sb; } };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 var cnt [26 ]int type hp struct { sort.IntSlice }func (h hp) int ) bool { return cnt[h.IntSlice[i]] > cnt[h.IntSlice[j]] }func (h *hp) interface {}) { h.IntSlice = append (h.IntSlice, v.(int )) }func (h *hp) interface {} { a := h.IntSlice; v := a[len (a)-1 ]; h.IntSlice = a[:len (a)-1 ]; return v }func (h *hp) int ) { heap.Push(h, v) }func (h *hp) int { return heap.Pop(h).(int ) }func reorganizeString (s string ) string { n := len (s) if n <= 1 { return s } cnt = [26 ]int {} maxCnt := 0 for _, ch := range s { ch -= 'a' cnt[ch]++ if cnt[ch] > maxCnt { maxCnt = cnt[ch] } } if maxCnt > (n+1 )/2 { return "" } h := &hp{} for i, c := range cnt[:] { if c > 0 { h.IntSlice = append (h.IntSlice, i) } } heap.Init(h) ans := make ([]byte , 0 , n) for len (h.IntSlice) > 1 { i, j := h.pop(), h.pop() ans = append (ans, byte ('a' +i), byte ('a' +j)) if cnt[i]--; cnt[i] > 0 { h.push(i) } if cnt[j]--; cnt[j] > 0 { h.push(j) } } if len (h.IntSlice) > 0 { ans = append (ans, byte ('a' +h.IntSlice[0 ])) } return string (ans) }
[sol1-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 class Solution : def reorganizeString (self, s: str ) -> str : if len (s) < 2 : return s length = len (s) counts = collections.Counter(s) maxCount = max (counts.items(), key=lambda x: x[1 ])[1 ] if maxCount > (length + 1 ) // 2 : return "" queue = [(-x[1 ], x[0 ]) for x in counts.items()] heapq.heapify(queue) ans = list () while len (queue) > 1 : _, letter1 = heapq.heappop(queue) _, letter2 = heapq.heappop(queue) ans.extend([letter1, letter2]) counts[letter1] -= 1 counts[letter2] -= 1 if counts[letter1] > 0 : heapq.heappush(queue, (-counts[letter1], letter1)) if counts[letter2] > 0 : heapq.heappush(queue, (-counts[letter2], letter2)) if queue: ans.append(queue[0 ][1 ]) return "" .join(ans)
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 var reorganizeString = function (s ) { if (s.length < 2 ) { return s; } const length = s.length ; const counts = _.countBy (s); const maxCount = Math .max (...Object .values (counts)); if (maxCount > Math .floor ((length + 1 ) / 2 )) { return '' ; } const queue = new MaxPriorityQueue (); Object .keys (counts).forEach (x =>enqueue (x, counts[x])); let ans = new Array (); while (queue.size () > 1 ) { const letter1 = queue.dequeue ()['element' ]; const letter2 = queue.dequeue ()['element' ]; ans = ans.concat (letter1, letter2) counts[letter1]--; counts[letter2]--; if (counts[letter1] > 0 ) { queue.enqueue (letter1, counts[letter1]); } if (counts[letter2] > 0 ) { queue.enqueue (letter2, counts[letter2]); } } if (queue.size ()) { ans.push (queue.dequeue ()['element' ]) } return ans.join ('' ); };
复杂度分析
时间复杂度:O(n\log|\Sigma| + |\Sigma|),其中 n 是字符串的长度,\Sigma 是字符集,在本题中字符集为所有小写字母,|\Sigma|=26。
空间复杂度:O(|\Sigma|),其中 \Sigma 是字符集,在本题中字符集为所有小写字母,|\Sigma|=26。这里不计算存储最终答案字符串需要的空间(以及由于语言特性,在构造字符串时需要的额外缓存空间),空间复杂度主要取决于统计每个字母出现次数的空间和最大堆空间。
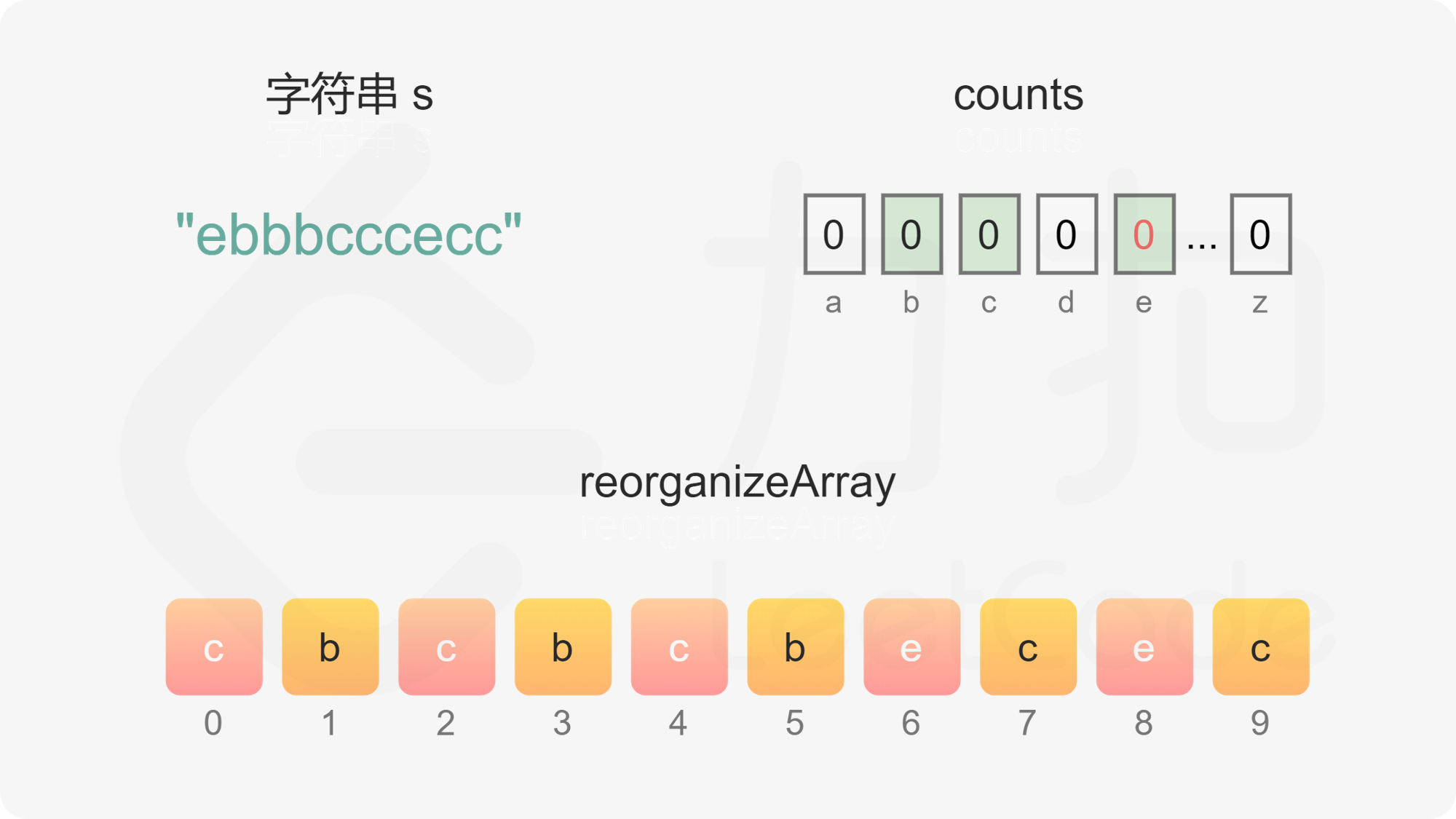
方法二:基于计数的贪心 首先统计每个字母的出现次数,然后根据每个字母的出现次数重构字符串。
当 n 是奇数且出现最多的字母的出现次数是 \dfrac{n+1/2 时,出现次数最多的字母必须全部放置在偶数下标,否则一定会出现相邻的字母相同的情况。其余情况下,每个字母放置在偶数下标或者奇数下标都是可行的。
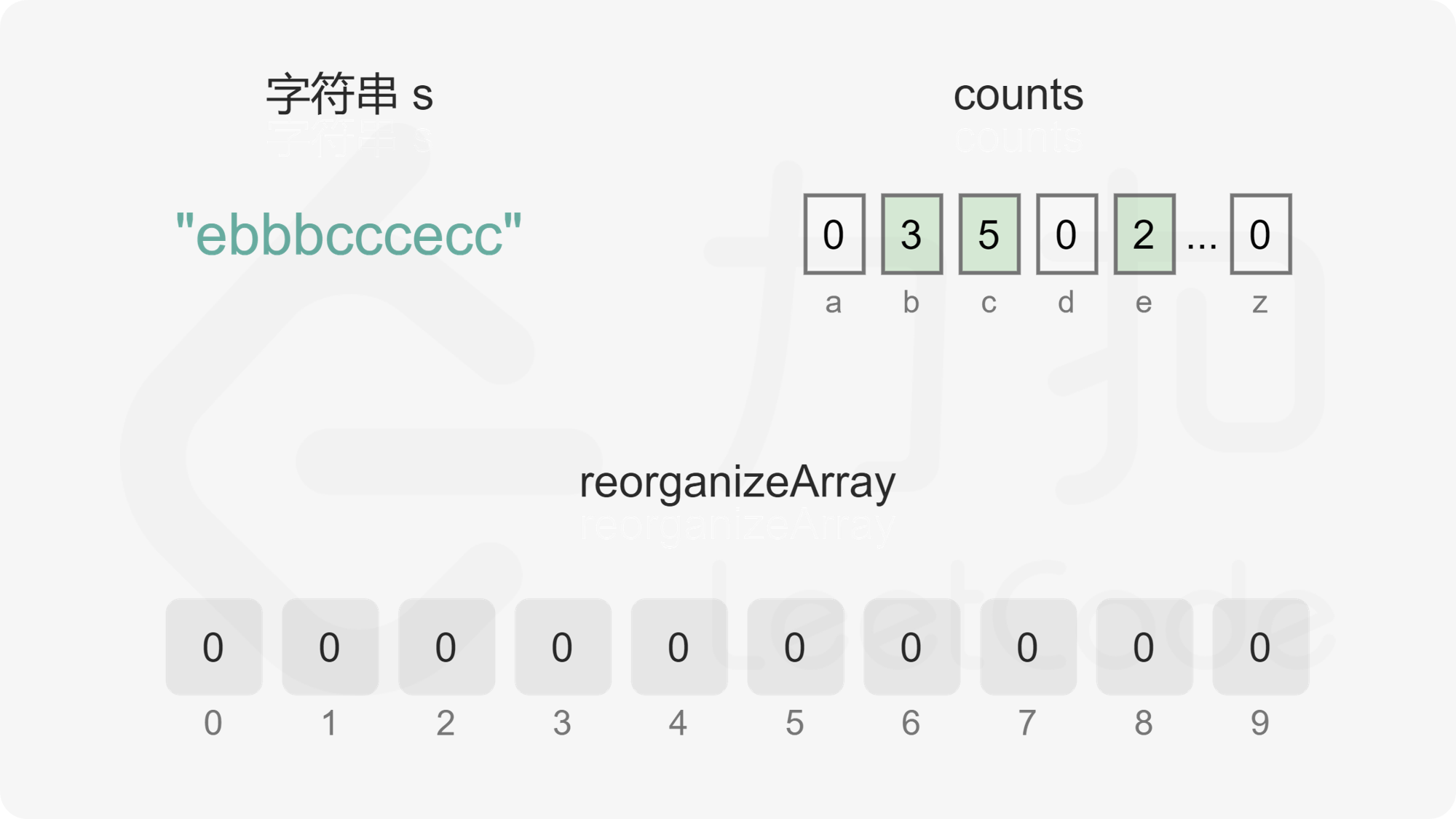
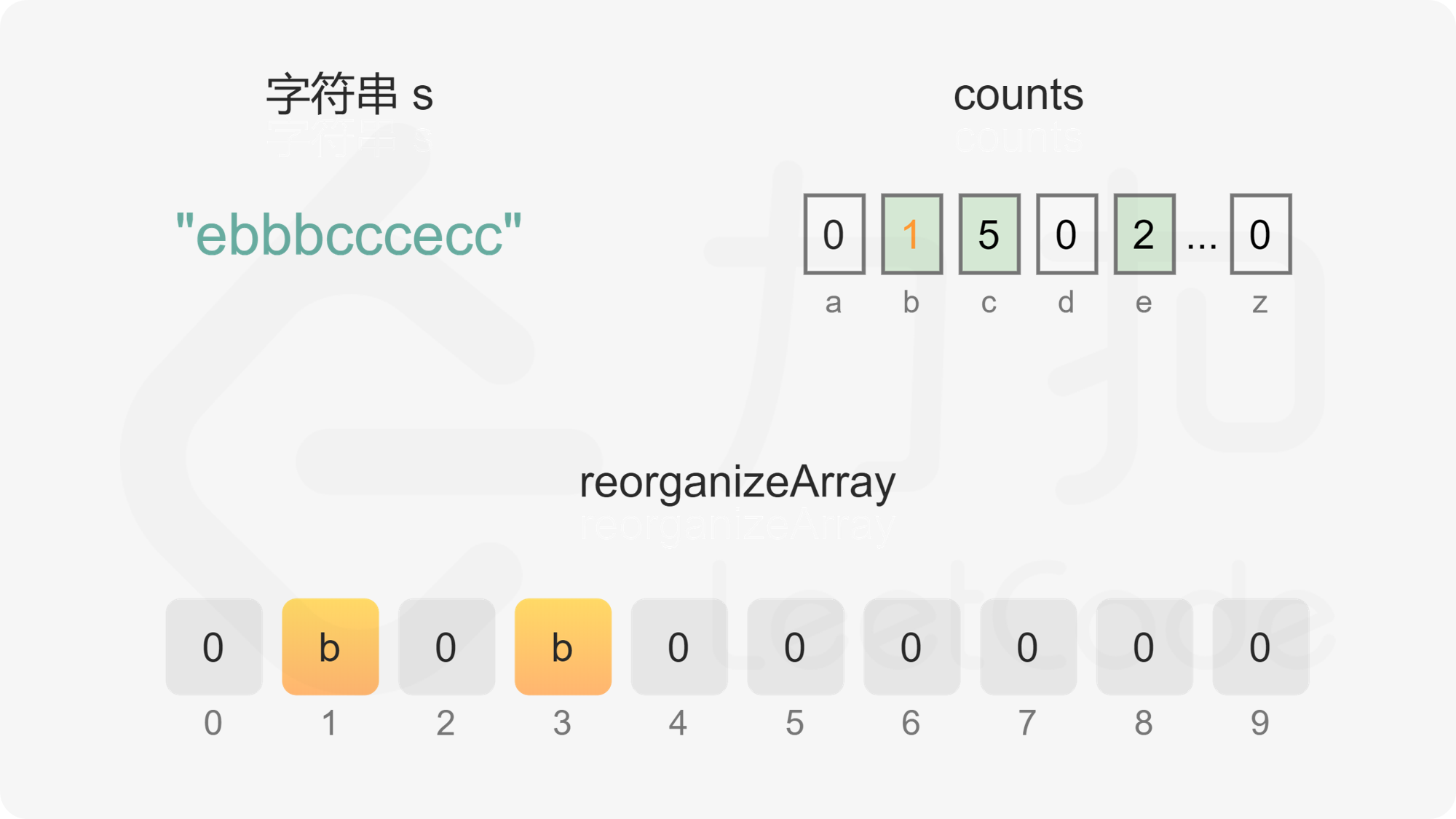
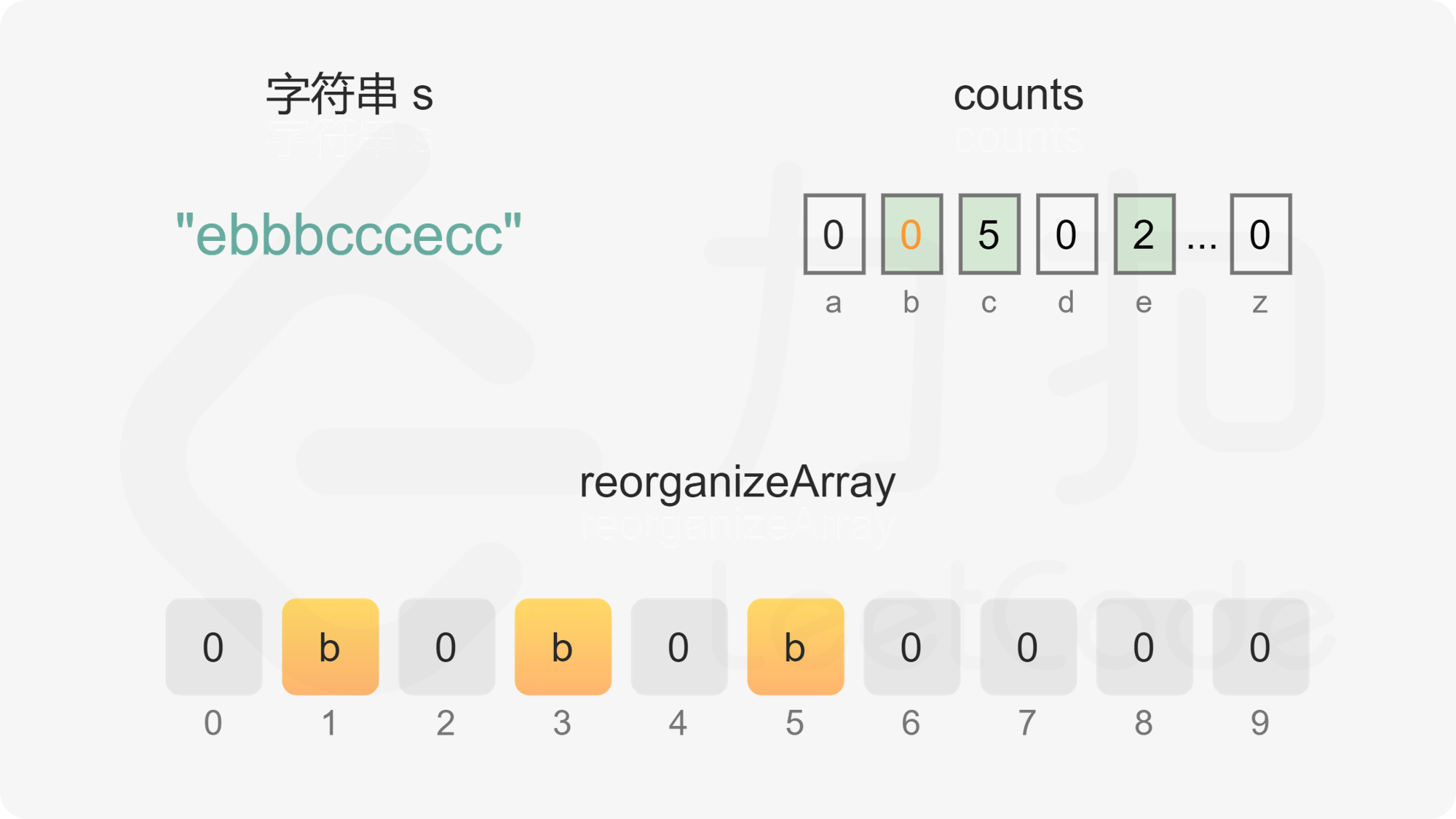
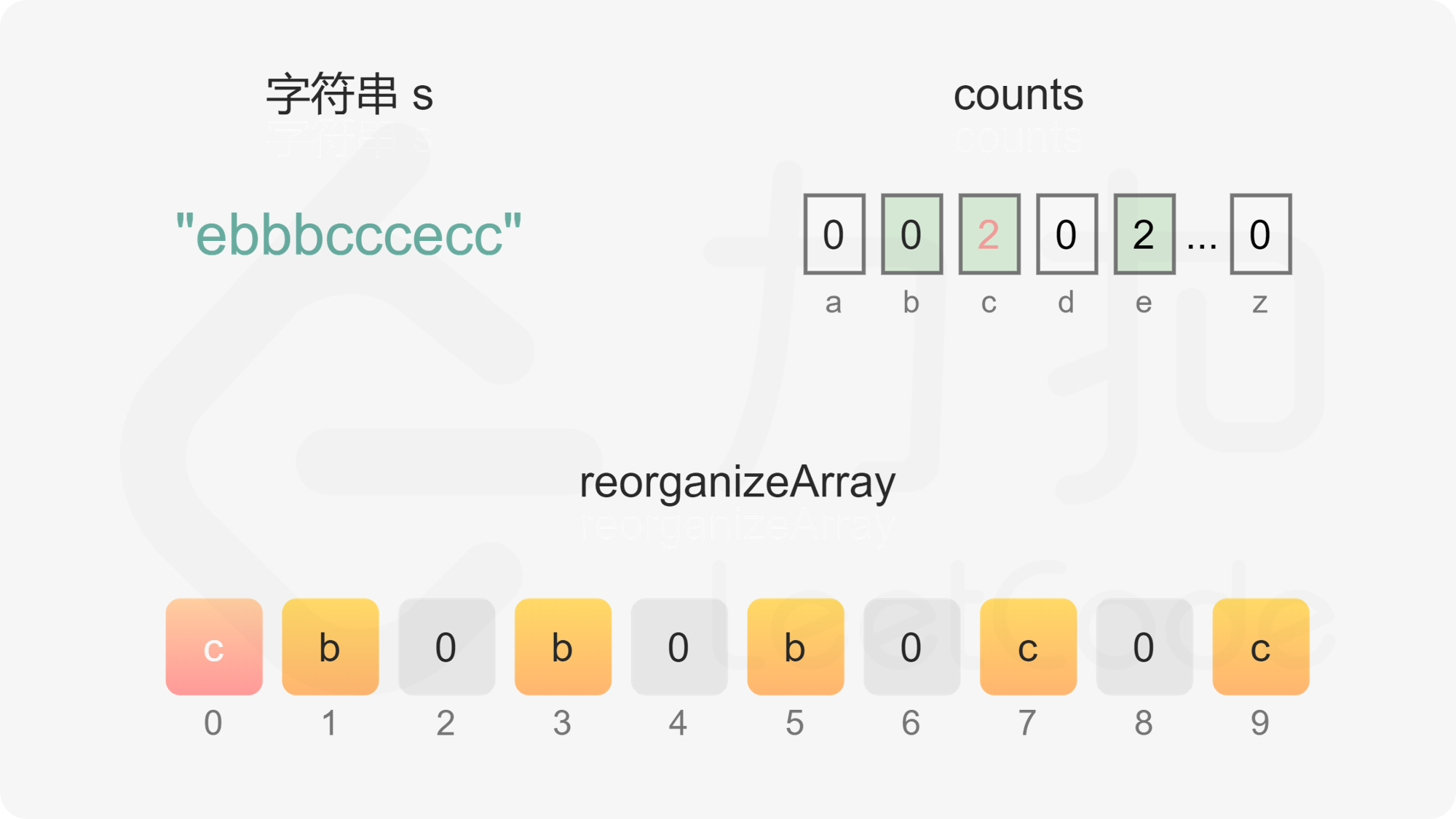
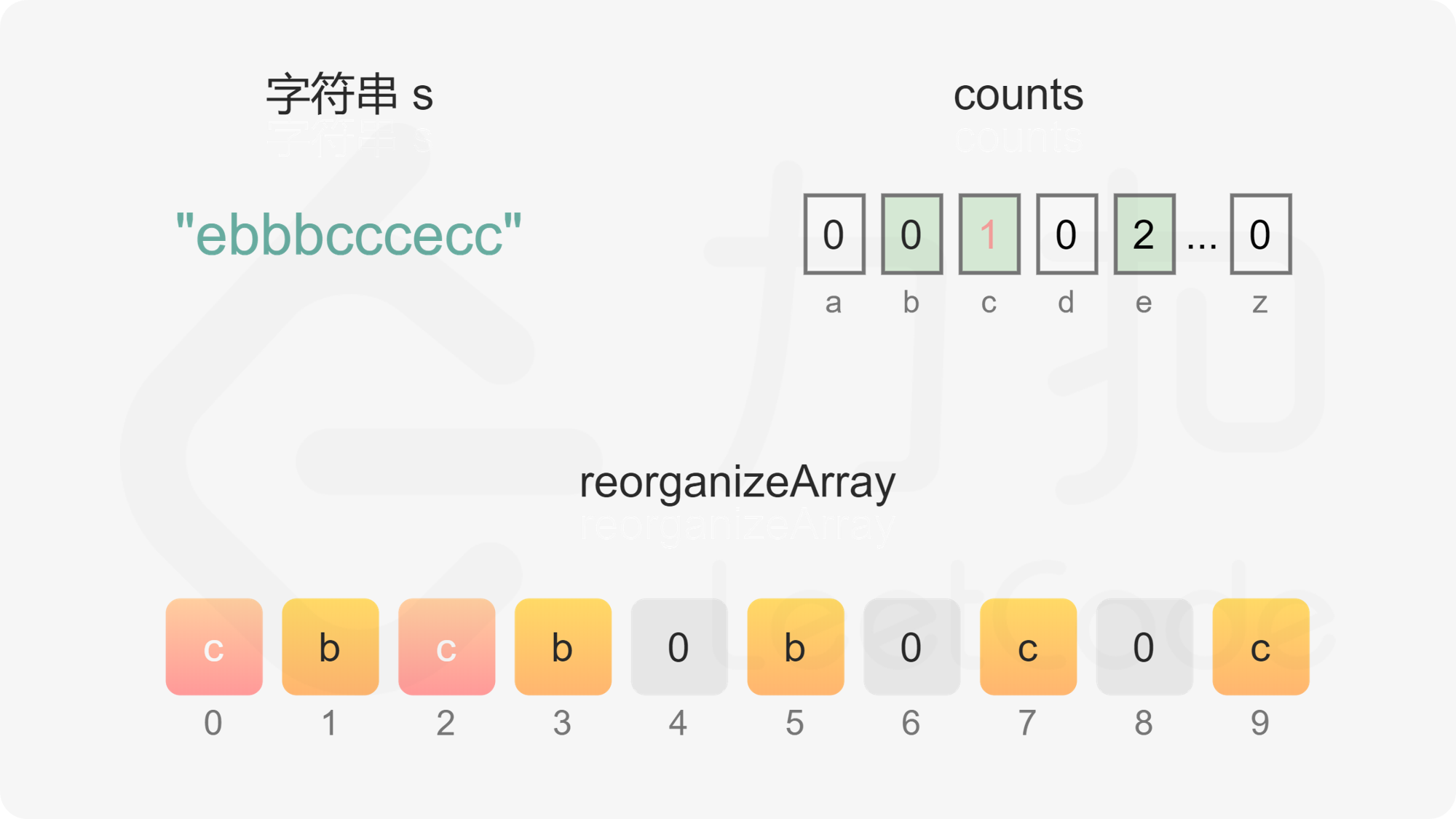
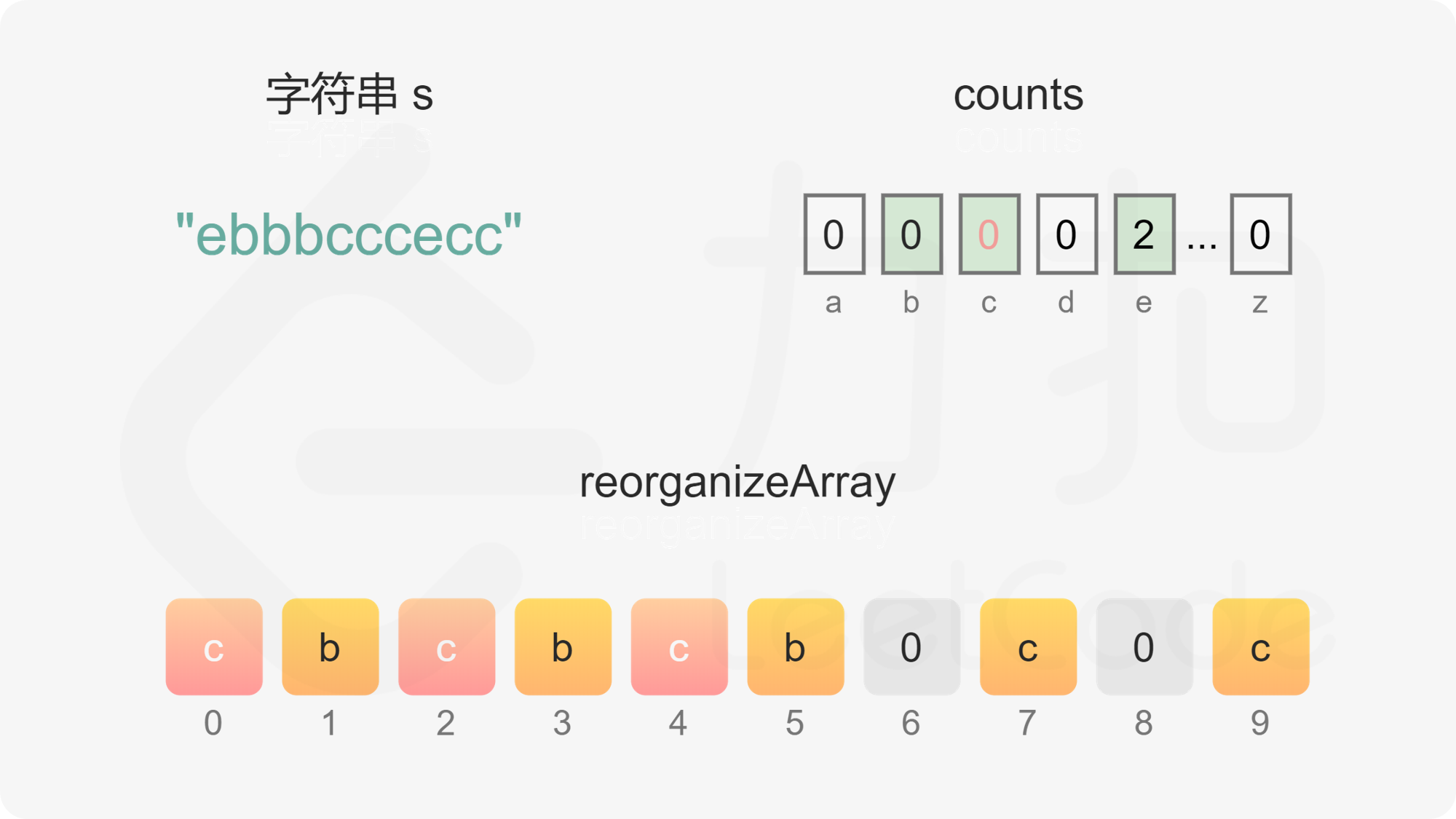
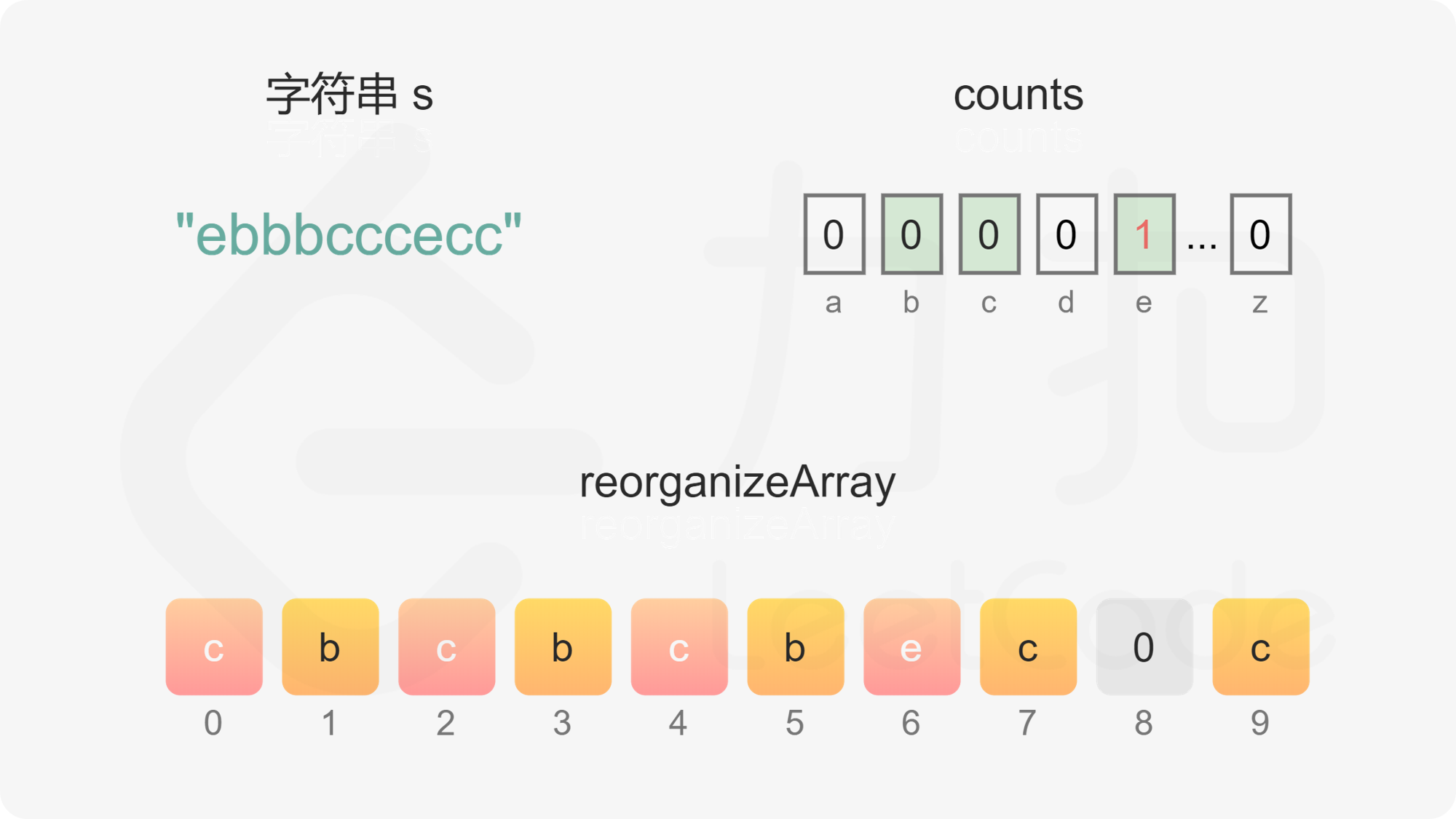
维护偶数下标 evenIndex 和奇数下标 oddIndex,初始值分别为 0 和 1。遍历每个字母,根据每个字母的出现次数判断字母应该放置在偶数下标还是奇数下标。
首先考虑是否可以放置在奇数下标。根据上述分析可知,只要字母的出现次数不超过字符串的长度的一半(即出现次数小于或等于 \Big\lfloor \dfrac{n}{2} \Big\rfloor),就可以放置在奇数下标,只有当字母的出现次数超过字符串的长度的一半时,才必须放置在偶数下标。字母的出现次数超过字符串的长度的一半只可能发生在 n 是奇数的情况下,且最多只有一个字母的出现次数会超过字符串的长度的一半。
因此通过如下操作在重构的字符串中放置字母。
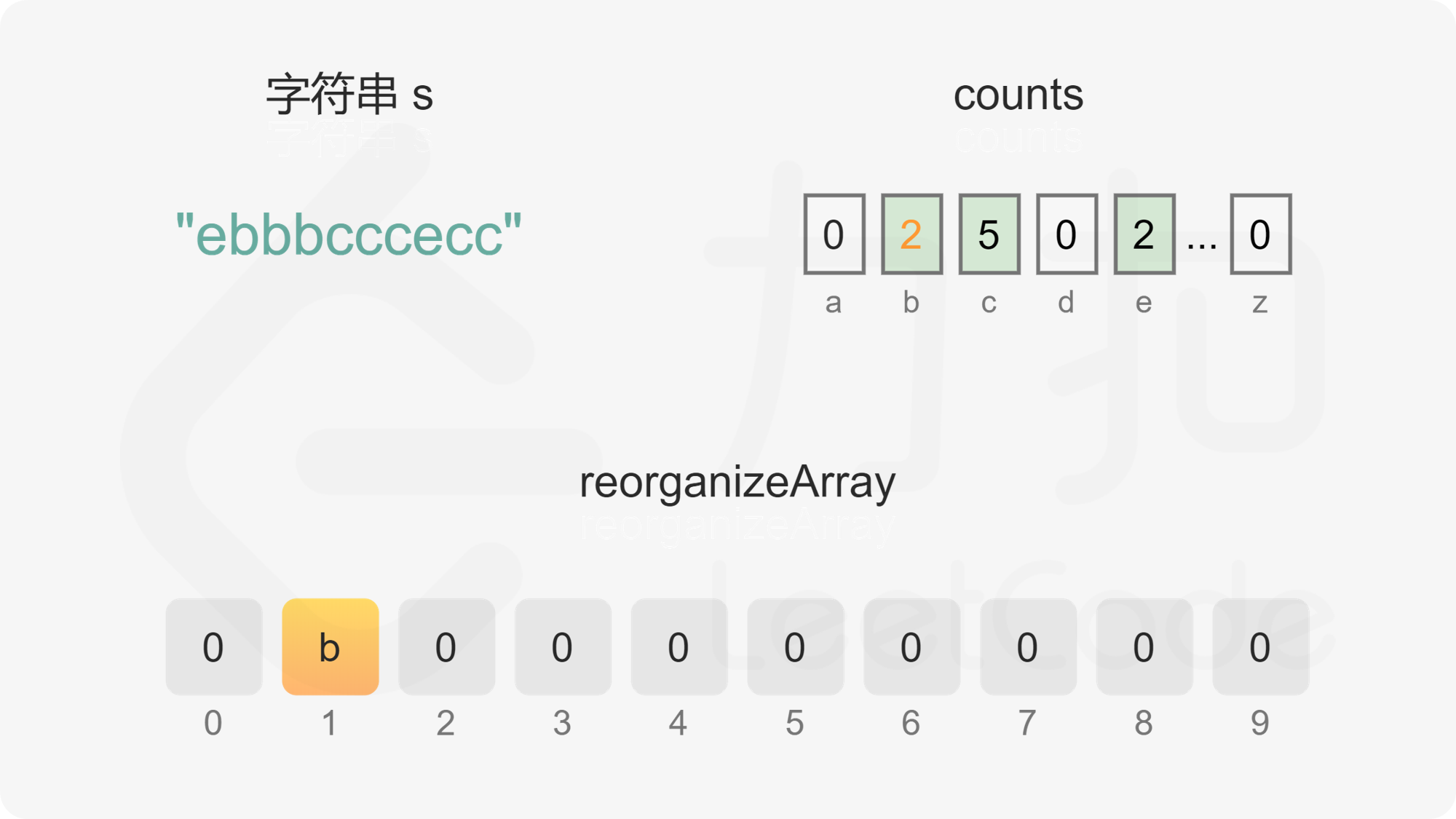
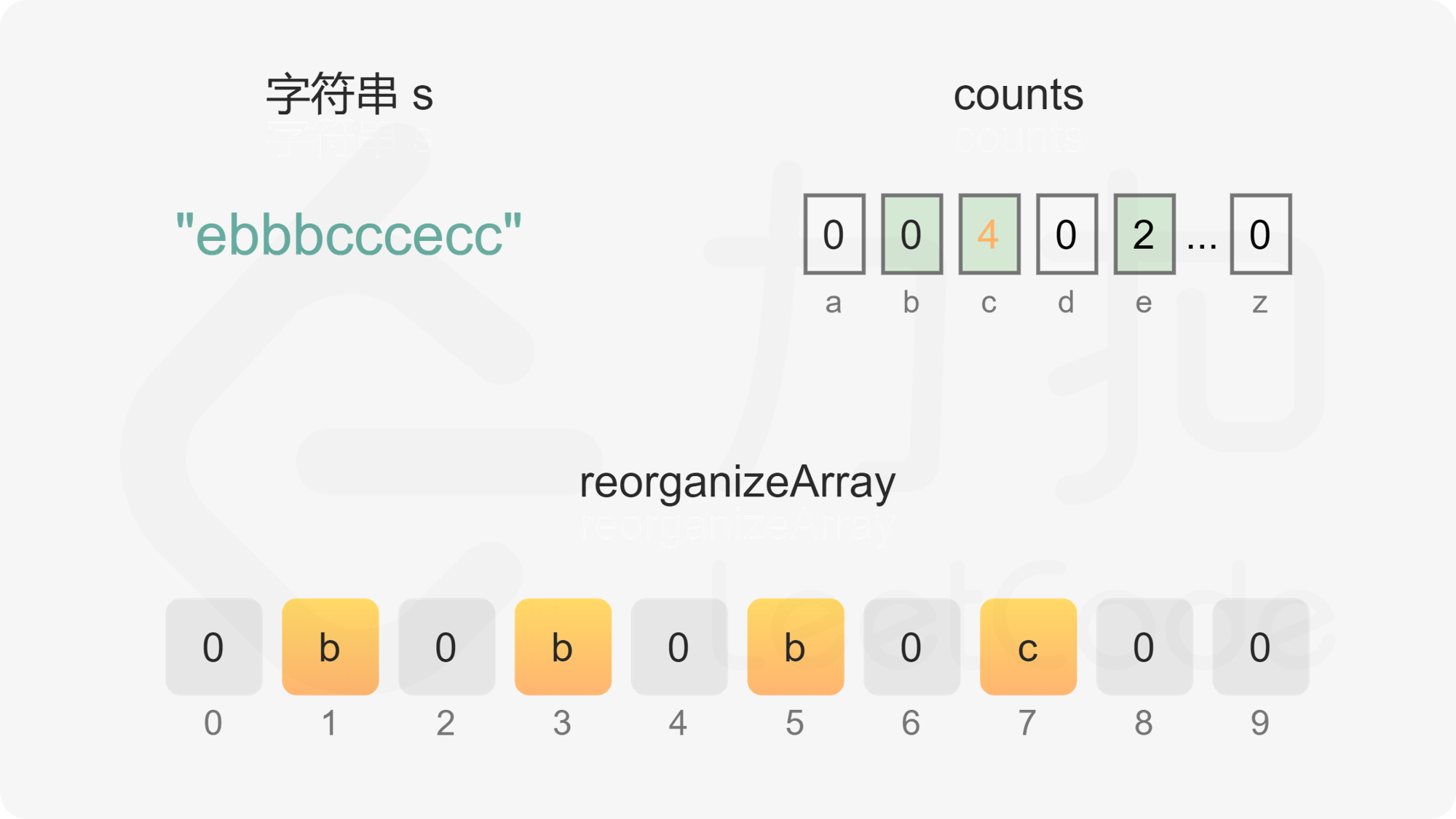
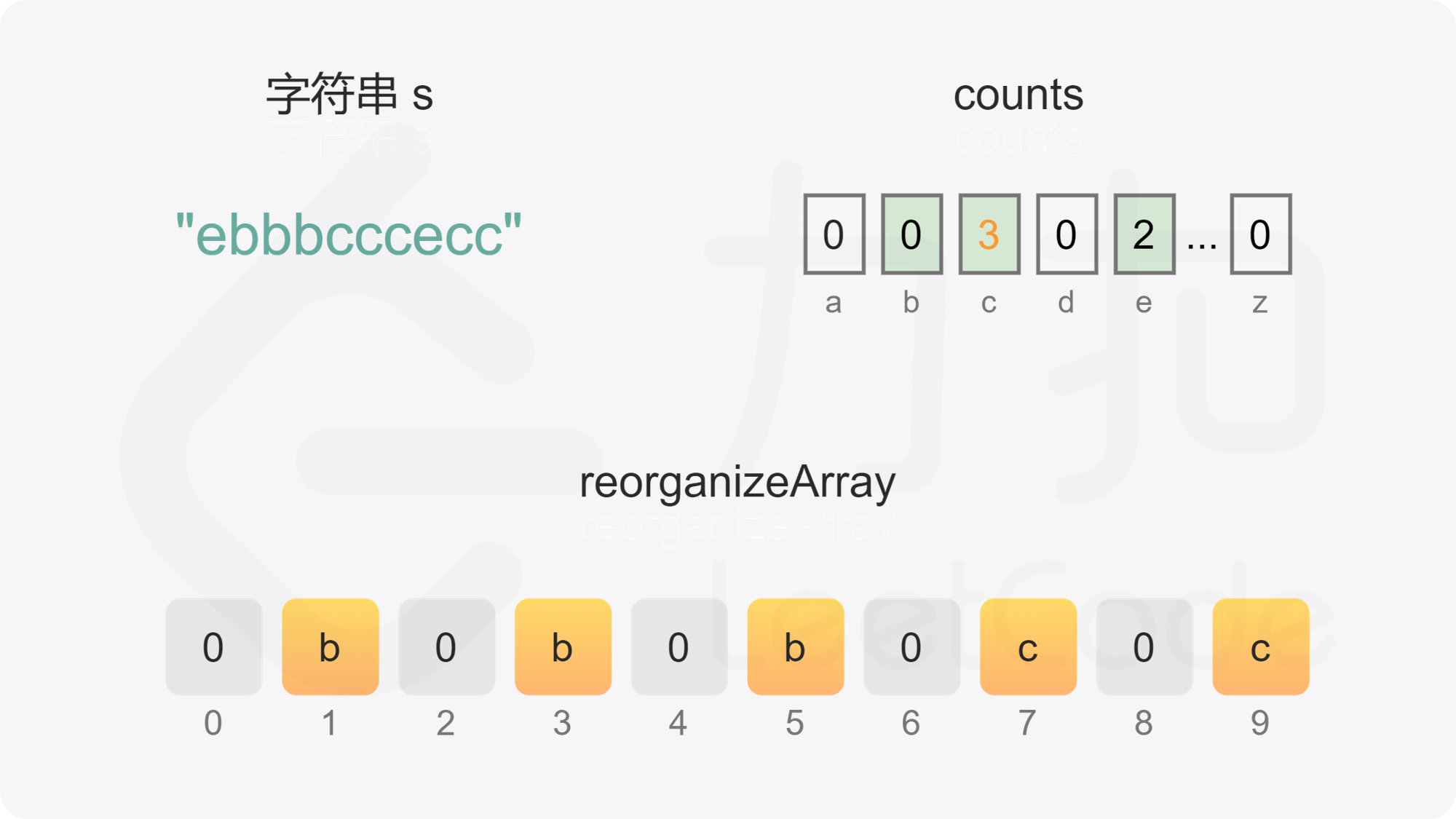
如果字母的出现次数大于 0 且小于或等于 \Big\lfloor \dfrac{n}{2} \Big\rfloor,且 oddIndex 没有超出数组下标范围,则将字母放置在 oddIndex,然后将 oddIndex 的值加 2。
如果字母的出现次数大于 \Big\lfloor \dfrac{n}{2} \Big\rfloor,或 oddIndex 超出数组下标范围,则将字母放置在 evenIndex,然后将 evenIndex 的值加 2。
如果一个字母出现了多次,则重复上述操作,直到该字母全部放置完毕。
那么上述做法是否可以确保相邻的字母都不相同?考虑以下三种情况。
如果 n 是奇数且存在一个字母的出现次数为 \dfrac{n+1/2,则该字母全部被放置在偶数下标,其余的 \dfrac{n-1/2 个字母都被放置在奇数下标,因此相邻的字母一定不相同。
如果同一个字母全部被放置在奇数下标或全部被放置在偶数下标,则该字母不可能在相邻的下标出现。
如果同一个字母先被放置在奇数下标直到奇数下标超出数组下标范围,然后被放置在偶数下标,由于该字母的出现次数不会超过 \Big\lfloor \dfrac{n}{2} \Big\rfloor,因此该字母的最小奇数下标与最大偶数下标之差不小于 3,不可能在相邻的下标出现。证明如下:
当 n 是偶数时,如果该字母的出现次数为 \dfrac{n}{2,包括 p 个奇数下标和 q 个偶数下标,满足 p+q=\dfrac{n}{2,最小奇数下标是 n-2p+1,最大偶数下标是 2(q-1),最小奇数下标与最大偶数下标之差为:
\begin{aligned}
当 n 是奇数时,如果该字母的出现次数为 \dfrac{n-1/2,包括 p 个奇数下标和 q 个偶数下标,满足 p+q=\dfrac{n-1/2,最小奇数下标是 n-2p,最大偶数下标是 2(q-1),最小奇数下标与最大偶数下标之差为:
\begin{aligned}
因此,在重构字符串可行的情况下,基于计数的贪心可以确保相邻的字母都不相同,得到正确答案。
<
[sol2-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 class Solution { public String reorganizeString (String s) { if (s.length() < 2 ) { return s; } int [] counts = new int [26 ]; int maxCount = 0 ; int length = s.length(); for (int i = 0 ; i < length; i++) { char c = s.charAt(i); counts[c - 'a' ]++; maxCount = Math.max(maxCount, counts[c - 'a' ]); } if (maxCount > (length + 1 ) / 2 ) { return "" ; } char [] reorganizeArray = new char [length]; int evenIndex = 0 , oddIndex = 1 ; int halfLength = length / 2 ; for (int i = 0 ; i < 26 ; i++) { char c = (char ) ('a' + i); while (counts[i] > 0 && counts[i] <= halfLength && oddIndex < length) { reorganizeArray[oddIndex] = c; counts[i]--; oddIndex += 2 ; } while (counts[i] > 0 ) { reorganizeArray[evenIndex] = c; counts[i]--; evenIndex += 2 ; } } return new String (reorganizeArray); } }
[sol2-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 public class Solution { public string ReorganizeString (string s if (s.Length < 2 ) { return s; } int [] counts = new int [26 ]; int maxCount = 0 ; int length = s.Length; for (int i = 0 ; i < length; i++) { char c = s[i]; counts[c - 'a' ]++; maxCount = Math.Max(maxCount, counts[c - 'a' ]); } if (maxCount > (length + 1 ) / 2 ) { return "" ; } char [] reorganizeArray = new char [length]; int evenIndex = 0 , oddIndex = 1 ; int halfLength = length / 2 ; for (int i = 0 ; i < 26 ; i++) { char c = (char ) ('a' + i); while (counts[i] > 0 && counts[i] <= halfLength && oddIndex < length) { reorganizeArray[oddIndex] = c; counts[i]--; oddIndex += 2 ; } while (counts[i] > 0 ) { reorganizeArray[evenIndex] = c; counts[i]--; evenIndex += 2 ; } } return new string (reorganizeArray); } }
[sol2-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Solution {public : string reorganizeString (string s) { if (s.length () < 2 ) { return s; } vector<int > counts (26 , 0 ) ; int maxCount = 0 ; int length = s.length (); for (int i = 0 ; i < length; i++) { char c = s[i]; counts[c - 'a' ]++; maxCount = max (maxCount, counts[c - 'a' ]); } if (maxCount > (length + 1 ) / 2 ) { return "" ; } string reorganizeArray (length, ' ' ) ; int evenIndex = 0 , oddIndex = 1 ; int halfLength = length / 2 ; for (int i = 0 ; i < 26 ; i++) { char c = 'a' + i; while (counts[i] > 0 && counts[i] <= halfLength && oddIndex < length) { reorganizeArray[oddIndex] = c; counts[i]--; oddIndex += 2 ; } while (counts[i] > 0 ) { reorganizeArray[evenIndex] = c; counts[i]--; evenIndex += 2 ; } } return reorganizeArray; } };
[sol2-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 func reorganizeString (s string ) string { n := len (s) if n <= 1 { return s } cnt := [26 ]int {} maxCnt := 0 for _, ch := range s { ch -= 'a' cnt[ch]++ if cnt[ch] > maxCnt { maxCnt = cnt[ch] } } if maxCnt > (n+1 )/2 { return "" } ans := make ([]byte , n) evenIdx, oddIdx, halfLen := 0 , 1 , n/2 for i, c := range cnt[:] { ch := byte ('a' + i) for c > 0 && c <= halfLen && oddIdx < n { ans[oddIdx] = ch c-- oddIdx += 2 } for c > 0 { ans[evenIdx] = ch c-- evenIdx += 2 } } return string (ans) }
[sol2-Python3] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 class Solution : def reorganizeString (self, s: str ) -> str : if len (s) < 2 : return s length = len (s) counts = collections.Counter(s) maxCount = max (counts.items(), key=lambda x: x[1 ])[1 ] if maxCount > (length + 1 ) // 2 : return "" reorganizeArray = ["" ] * length evenIndex, oddIndex = 0 , 1 halfLength = length // 2 for c, count in counts.items(): while count > 0 and count <= halfLength and oddIndex < length: reorganizeArray[oddIndex] = c count -= 1 oddIndex += 2 while count > 0 : reorganizeArray[evenIndex] = c count -= 1 evenIndex += 2 return "" .join(reorganizeArray)
[sol2-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 const getIdx = (c ) => c.charCodeAt () - 'a' .charCodeAt ();const getAlpha = (c ) => String .fromCharCode (c);var reorganizeString = function (s ) { if (s.length < 2 ) { return s; } const counts = new Array (26 ).fill (0 ); let maxCount = 0 ; const length = s.length ; for (let i = 0 ; i < length; i++) { const c = s.charAt (i); counts[getIdx (c)]++; maxCount = Math .max (maxCount, counts[getIdx (c)]); } if (maxCount > Math .floor ((length + 1 ) / 2 )) { return "" ; } const reorganizeArray = new Array (length); let evenIndex = 0 , oddIndex = 1 ; const halfLength = Math .floor (length / 2 ); for (let i = 0 ; i < 26 ; i++) { const c = getAlpha ('a' .charCodeAt () + i); while (counts[i] > 0 && counts[i] <= halfLength && oddIndex < length) { reorganizeArray[oddIndex] = c; counts[i]--; oddIndex += 2 ; } while (counts[i] > 0 ) { reorganizeArray[evenIndex] = c; counts[i]--; evenIndex += 2 ; } } return reorganizeArray.join ('' ); };
[sol2-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 char * reorganizeString (char * s) { int n = strlen (s); if (n < 2 ) { return s; } int counts[26 ]; memset (counts, 0 , sizeof (counts)); int maxCount = 0 ; for (int i = 0 ; i < n; i++) { char c = s[i]; counts[c - 'a' ]++; maxCount = fmax(maxCount, counts[c - 'a' ]); } if (maxCount > (n + 1 ) / 2 ) { return "" ; } char * reorganizeArray = malloc (sizeof (char ) * (n + 1 )); for (int i = 0 ; i < n; i++) { reorganizeArray[i] = ' ' ; } reorganizeArray[n] = '\0' ; int evenIndex = 0 , oddIndex = 1 ; int halfLength = n / 2 ; for (int i = 0 ; i < 26 ; i++) { char c = 'a' + i; while (counts[i] > 0 && counts[i] <= halfLength && oddIndex < n) { reorganizeArray[oddIndex] = c; counts[i]--; oddIndex += 2 ; } while (counts[i] > 0 ) { reorganizeArray[evenIndex] = c; counts[i]--; evenIndex += 2 ; } } return reorganizeArray; }
复杂度分析
时间复杂度:O(n+|\Sigma|),其中 n 是字符串的长度,\Sigma 是字符集,在本题中字符集为所有小写字母,|\Sigma|=26。
空间复杂度:O(|\Sigma|),其中 n 是字符串的长度,\Sigma 是字符集,在本题中字符集为所有小写字母,|\Sigma|=26。空间复杂度主要取决于统计每个字母出现次数的空间。这里不计算存储最终答案字符串需要的空间(以及由于语言特性,在构造字符串时需要的额外缓存空间)。
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
> ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>