0773-滑动谜题

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

在一个 2 x 3 的板上（board）有 5 块砖瓦，用数字 1~5 来表示, 以及一块空缺用 0 来表示。一次 移动 定义为选择
0 与一个相邻的数字（上下左右）进行交换.

最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。

给出一个谜板的初始状态 board ，返回最少可以通过多少次移动解开谜板，如果不能解开谜板，则返回 -1 。

示例 1：

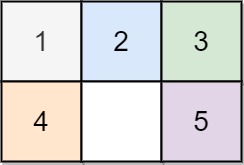
**输入：** board = [[1,2,3],[4,0,5]]
**输出：** 1
**解释：** 交换 0 和 5 ，1 步完成

示例 2:

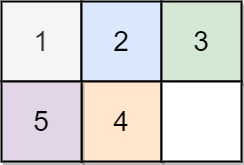
**输入：** board = [[1,2,3],[5,4,0]]
**输出：** -1
**解释：** 没有办法完成谜板

示例 3:

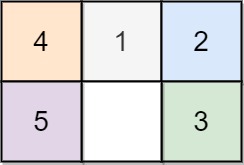
**输入：** board = [[4,1,2],[5,0,3]]
**输出：** 5
**解释：**
最少完成谜板的最少移动次数是 5 ，
一种移动路径:
尚未移动: [[4,1,2],[5,0,3]]
移动 1 次: [[4,1,2],[0,5,3]]
移动 2 次: [[0,1,2],[4,5,3]]
移动 3 次: [[1,0,2],[4,5,3]]
移动 4 次: [[1,2,0],[4,5,3]]
移动 5 次: [[1,2,3],[4,5,0]]

提示：

  • board.length == 2
  • board[i].length == 3
  • 0 <= board[i][j] <= 5
  • board[i][j] 中每个值都 不同

方法一：广度优先搜索

思路与算法

我们可以使用广度优先搜索，找出从初始状态 board 到目标状态 [[1,2,3],[4,5,0]] 的最小交换次数。

具体地，我们在一开始将 (\textit{board}, 0) 加入队列，并使用该队列进行广度优先搜索。在搜索的过程中，设当前搜索到的状态为 status，操作的次数为 step，我们可以枚举 status 通过一次操作得到的状态。设其中的某个状态为 next_status，如果其没有被搜索过，我们就将 (\textit{next_status}, \textit{step} + 1) 加入队列。如果搜索到了 target，我们就返回其对应的操作次数。

在搜索的过程中，我们需要一个哈希表存储所有搜索到的状态，避免重复搜索。

如果搜索完成后，我们仍没有搜索到 [[1,2,3],[4,5,0]]，说明我们无法解开谜板，返回 -1。

细节

本题中，搜索的状态 status 是一个 2\times 3 的二维数组，在很多语言中，我们无法将数组直接放入哈希表中，可行的解决方案有两种：

  • 自行实现数组的哈希函数；

  • 将数组转换成语言中可以直接进行哈希的类型。

在问题中，我们使用第二种解决方案，将 status 按照行优先的顺序拼接成一个长度为 2\times 3=6 的字符串。例如目标状态 [[1,2,3],[4,5,0]] 可以表示为 123450。

在确定了解决方案后，我们还需要考虑如何有效地找出 status 通过一次操作得到的所有状态。根据题目中的规定，每一次操作可以将 status 中的 0 与相邻位置的数字进行交换，因此我们同样可以按照行优先的顺序给 2\times 3 的谜板进行编号：

fig1{:width=”50%”}

这样一来，我们可以预处理出每一个位置的所有相邻位置，即：

  • 0 的相邻位置是 1, 3；
  • 1 的相邻位置是 0, 2, 4；
  • 2 的相邻位置是 1, 5；
  • 3 的相邻位置是 0, 4；
  • 4 的相邻位置是 1, 3, 5；
  • 5 的相邻位置是 2, 4。

因此，我们在 status 中找出 0 所在的位置 x，对于每一个与 x 相邻的位置 y，我们将 status}[x] 与 status}[y] 进行交换，即等同于进行了一次操作。注意：这里的 status 是已经拼接完成的字符串。

最后我们还需要注意一个细节：如果 board 就是目标状态 [[1,2,3],[4,5,0]]，那么直接返回答案 0。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Solution {
private:
    vector<vector<int>> neighbors = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};

public:
    int slidingPuzzle(vector<vector<int>>& board) {
        // 枚举 status 通过一次交换操作得到的状态
        auto get = [&](string& status) -> vector<string> {
            vector<string> ret;
            int x = status.find('0');
            for (int y: neighbors[x]) {
                swap(status[x], status[y]);
                ret.push_back(status);
                swap(status[x], status[y]);
            }
            return ret;
        };

        string initial;
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 3; ++j) {
                initial += char(board[i][j] + '0');
            }
        }
        if (initial == "123450") {
            return 0;
        }

        queue<pair<string, int>> q;
        q.emplace(initial, 0);
        unordered_set<string> seen = {initial};

        while (!q.empty()) {
            auto [status, step] = q.front();
            q.pop();
            for (auto&& next_status: get(status)) {
                if (!seen.count(next_status)) {
                    if (next_status == "123450") {
                        return step + 1;
                    }
                    q.emplace(next_status, step + 1);
                    seen.insert(move(next_status));
                }
            }
        }

        return -1;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
class Solution {
    int[][] neighbors = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};

    public int slidingPuzzle(int[][] board) {
        StringBuffer sb = new StringBuffer();
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 3; ++j) {
                sb.append(board[i][j]);
            }
        }
        String initial = sb.toString();
        if ("123450".equals(initial)) {
            return 0;
        }

        int step = 0;
        Queue<String> queue = new LinkedList<String>();
        queue.offer(initial);
        Set<String> seen = new HashSet<String>();
        seen.add(initial);

        while (!queue.isEmpty()) {
            ++step;
            int size = queue.size();
            for (int i = 0; i < size; ++i) {
                String status = queue.poll();
                for (String nextStatus : get(status)) {
                    if (!seen.contains(nextStatus)) {
                        if ("123450".equals(nextStatus)) {
                            return step;
                        }
                        queue.offer(nextStatus);
                        seen.add(nextStatus);
                    }
                }
            }
        }

        return -1;
    }

    // 枚举 status 通过一次交换操作得到的状态
    public List<String> get(String status) {
        List<String> ret = new ArrayList<String>();
        char[] array = status.toCharArray();
        int x = status.indexOf('0');
        for (int y : neighbors[x]) {
            swap(array, x, y);
            ret.add(new String(array));
            swap(array, x, y);
        }
        return ret;
    }

    public void swap(char[] array, int x, int y) {
        char temp = array[x];
        array[x] = array[y];
        array[y] = temp;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
public class Solution {
    int[][] neighbors = new int[6][]{new[]{1, 3}, new[]{0, 2, 4}, new[]{1, 5}, new[]{0, 4}, new[]{1, 3, 5}, new[]{2, 4}};

    public int SlidingPuzzle(int[][] board) {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 3; ++j) {
                sb.Append(board[i][j]);
            }
        }
        string initial = sb.ToString();
        if ("123450".Equals(initial)) {
            return 0;
        }

        int step = 0;
        Queue<string> queue = new Queue<string>();
        queue.Enqueue(initial);
        ISet<string> seen = new HashSet<string>();
        seen.Add(initial);

        while (queue.Count > 0) {
            ++step;
            int size = queue.Count;
            for (int i = 0; i < size; ++i) {
                string status = queue.Dequeue();
                foreach (string nextStatus in Get(status)) {
                    if (!seen.Contains(nextStatus)) {
                        if ("123450".Equals(nextStatus)) {
                            return step;
                        }
                        queue.Enqueue(nextStatus);
                        seen.Add(nextStatus);
                    }
                }
            }
        }

        return -1;
    }

    // 枚举 status 通过一次交换操作得到的状态
    public IList<string> Get(string status) {
        IList<string> ret = new List<string>();
        char[] array = status.ToCharArray();
        int x = status.IndexOf('0');
        foreach (int y in neighbors[x]) {
            Swap(array, x, y);
            ret.Add(new string(array));
            Swap(array, x, y);
        }
        return ret;
    }

    public void Swap(char[] array, int x, int y) {
        char temp = array[x];
        array[x] = array[y];
        array[y] = temp;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution:
    NEIGHBORS = [[1, 3], [0, 2, 4], [1, 5], [0, 4], [1, 3, 5], [2, 4]]

    def slidingPuzzle(self, board: List[List[int]]) -> int:
        # 枚举 status 通过一次交换操作得到的状态
        def get(status: str) -> Generator[str, None, None]:
            s = list(status)
            x = s.index("0")
            for y in Solution.NEIGHBORS[x]:
                s[x], s[y] = s[y], s[x]
                yield "".join(s)
                s[x], s[y] = s[y], s[x]

        initial = "".join(str(num) for num in sum(board, []))
        if initial == "123450":
            return 0

        q = deque([(initial, 0)])
        seen = {initial}
        while q:
            status, step = q.popleft()
            for next_status in get(status):
                if next_status not in seen:
                    if next_status == "123450":
                        return step + 1
                    q.append((next_status, step + 1))
                    seen.add(next_status)
        
        return -1
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
var slidingPuzzle = function(board) {
    const neighbors = [[1, 3], [0, 2, 4], [1, 5], [0, 4], [1, 3, 5], [2, 4]];

    const sb = [];
    for (let i = 0; i < 2; ++i) {
        for (let j = 0; j < 3; ++j) {
            sb.push(board[i][j]);
        }
    }
    const initial = sb.join('');
    if ("123450" === initial) {
        return 0;
    }

    let step = 0;
    const queue = [];
    queue.push(initial);
    const seen = new Set();
    seen.add(initial);

    // 枚举 status 通过一次交换操作得到的状态
    const get = (status) => {
        const ret = [];
        const array = Array.from(status);
        const x = status.indexOf('0');
        for (const y of neighbors[x]) {
            [array[x], array[y]] = [array[y], array[x]];
            ret.push(array.join(''));
            [array[x], array[y]] = [array[y], array[x]];
        }
        return ret;
    }

    while (queue.length) {
        ++step;
        const size = queue.length;
        for (let i = 0; i < size; ++i) {
            const status = queue.shift();
            for (const nextStatus of get(status)) {
                if (!seen.has(nextStatus)) {
                    if ("123450" === nextStatus) {
                        return step;
                    }
                    queue.push(nextStatus);
                    seen.add(nextStatus);
                }
            }
        }
    }

    return -1;
};
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
var neighbors = [6][]int{{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}}

func slidingPuzzle(board [][]int) int {
    const target = "123450"

    s := make([]byte, 0, 6)
    for _, r := range board {
        for _, v := range r {
            s = append(s, '0'+byte(v))
        }
    }
    start := string(s)
    if start == target {
        return 0
    }

    // 枚举 status 通过一次交换操作得到的状态
    get := func(status string) (ret []string) {
        s := []byte(status)
        x := strings.Index(status, "0")
        for _, y := range neighbors[x] {
            s[x], s[y] = s[y], s[x]
            ret = append(ret, string(s))
            s[x], s[y] = s[y], s[x]
        }
        return
    }

    type pair struct {
        status string
        step   int
    }
    q := []pair{{start, 0}}
    seen := map[string]bool{start: true}
    for len(q) > 0 {
        p := q[0]
        q = q[1:]
        for _, nxt := range get(p.status) {
            if !seen[nxt] {
                if nxt == target {
                    return p.step + 1
                }
                seen[nxt] = true
                q = append(q, pair{nxt, p.step + 1})
            }
        }
    }
    return -1
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
struct HashTable {
    char str[7];
    UT_hash_handle hh;
};

struct Node {
    char str[7];
    int val;
};

const int neighbors[6][3] = {{1, 3, -1}, {0, 2, 4}, {1, 5, -1}, {0, 4, -1}, {1, 3, 5}, {2, 4, -1}};

void swap(char* x, char* y) {
    char t = *x;
    *x = *y, *y = t;
}

// 枚举 status 通过一次旋转得到的数字
char** getNextStatus(char* status, int* retSize) {
    char** ret = malloc(sizeof(char*) * 3);
    *retSize = 0;
    int x = 0;
    while (status[x] != '0') {
        x++;
    }
    for (int i = 0; i < 3 && neighbors[x][i] != -1; i++) {
        int y = neighbors[x][i];
        swap(&status[x], &status[y]);
        ret[(*retSize)] = malloc(sizeof(char) * 7);
        strcpy(ret[(*retSize)++], status);
        swap(&status[x], &status[y]);
    }
    return ret;
}

int slidingPuzzle(int** board, int boardSize, int* boardColSize) {
    char str_0[] = "123450";
    char initial[7];
    for (int i = 0; i < 2; ++i) {
        for (int j = 0; j < 3; ++j) {
            initial[i * 3 + j] = (char)(board[i][j] + '0');
        }
    }
    initial[6] = '\0';
    if (strcmp(initial, str_0) == 0) {
        return 0;
    }

    struct Node q[10001];
    int left = 0, right = 0;
    strcpy(q[right].str, initial);
    q[right++].val = 0;

    struct HashTable* seen = NULL;
    struct HashTable* tmp = malloc(sizeof(struct HashTable));
    strcpy(tmp->str, initial);
    HASH_ADD(hh, seen, str, sizeof(char) * 7, tmp);

    while (left < right) {
        char* status = q[left].str;
        int step = q[left++].val;
        int nextStatusSize;
        char** nextStatus = getNextStatus(status, &nextStatusSize);
        for (int i = 0; i < nextStatusSize; i++) {
            HASH_FIND(hh, seen, nextStatus[i], sizeof(char) * 5, tmp);
            if (tmp == NULL) {
                if (strcmp(nextStatus[i], str_0) == 0) {
                    return step + 1;
                }
                strcpy(q[right].str, nextStatus[i]);
                q[right++].val = step + 1;
                tmp = malloc(sizeof(struct HashTable));
                strcpy(tmp->str, nextStatus[i]);
                HASH_ADD(hh, seen, str, sizeof(char) * 5, tmp);
            }
        }
    }

    return -1;
}

复杂度分析

  • 时间复杂度：O((mn)! \cdot mn)，其中 m 和 n 分别是谜板的行数和列数，在本题中 m=2，n=3。谜板的状态的可能性一共有 (mn)! 种，这也是我们可以搜索到的状态数上限。对于每一个状态，我们需要 O(mn) 的时间找出 0 的位置，其最多可以和四个方向上相邻的数字进行交换，共需要 O(4mn) = O(mn) 的时间生成操作后的新状态，因此广度优先搜索的总时间复杂度为 O((mn)! \cdot mn)。

  • 空间复杂度：O((mn)! \cdot mn)。我们最多需要在队列中存储 O((mn)!) 个长度为 mn 的字符串。

方法二：启发式搜索

概念

我们可以使用启发式搜索更快地找到最小旋转次数。这里我们可以使用 A* 算法。

读者可以自行查阅资料学习关于 A* 算法的基础知识，例如 Wikipedia - A* search algorithm 或 oi-wiki - A* 。它不是本题解的重点，因此这里不再赘述。读者可以阅读下面的段落检验自己的学习成果：

在 A* 算法中，我们需要使用四个距离函数 F(x), G(x), H(x), H^*(x)，其中 F(x), G(x), H(x) 是可以求出的，而 H^*(x) 是无法求出的，我们需要用 H(x) 近似 H^*(x)。设起点为 s，终点为 t，这些距离函数的意义如下：

  • G(x) 表示从起点 s 到节点 x 的「实际」路径长度，注意 G(x) 并不一定是最短的；

  • H(x) 表示从节点 x 到终点 t 的「估计」最短路径长度，称为启发函数；

  • H^*(x) 表示从节点 x 到终点 t 的「实际」最短路径长度，这是我们在广度优先搜索的过程中无法求出的，我们需要用 H(x) 近似 H^*(x)；

  • F(x) 满足 F(x) = G(x) + H(x)，即为从起点 s 到终点 t 的「估计」路径长度。我们总是挑选出最小的 F(x) 对应的 x 进行搜索，因此 A* 算法需要借助优先队列来实现。

如果读者熟悉求解最短路的 Dijkstra 算法，就可以发现 Dijkstra 算法是 A* 算法在 H(x) \equiv 0 时的特殊情况。

A* 算法具有两个性质：

  • 如果对于任意的节点 x，H(x) \leq H^*(x) 恒成立，即我们「估计」出的从节点 x 到终点 t 的最短路径长度总是不超过「实际」的最短路径长度，那么称启发函数 H(x) 是可接纳的（admissible heuristic）。在这种情况下，A* 算法一定能找到最短路，但同一节点可能需要加入优先队列并搜索多次，即当我们从优先队列中取出节点 x 时，G(x) 并不一定等于从起点到节点 x 的「实际」最短路径的长度；

  • 如果对于任意的两个节点 x 和 y，并且 x 到 y 有一条长度为 D(x, y) 的有向边，H(x) - H(y) \leq D(x, y) 恒成立，并且 H(t)=0，那么称启发函数 H(x) 是一致的（consistent heuristic）。可以证明，一致的启发函数一定也是可接纳的。在这种情况下，同一节点只会被加入优先队列一次，并搜索不超过一次，即当我们从优先队列中取出节点 x 时，G(x) 一定等于从起点到节点 x 的「实际」最短路径的长度。

思路与算法

我们可以设计如下的启发函数：

H(\textit{status}) = \sum_{i=1}^5
\big(\textit{status}~ 中数字 i 的位置与目标状态中数字 i 的位置之间的曼哈顿距离\big)

在一次操作中，我们交换数字 0 和数字 i，非 0 的数字中只有数字 i 的位置发生了变化。那么要想将数字 i 从初始状态中的位置移动到目标状态中的位置，我们至少需要进行「这两个位置之间的曼哈顿距离」次操作，因此我们解开谜板的需要的最少操作次数的下界为 H(\textit{status})。

根据定义，对于状态 status 和其通过一次操作得到的状态 next_status，H(\textit{status}) - H(\textit{next_status}) 要么为 1（数字 i 与其在目标状态中位置的曼哈顿距离减少了 1），要么为 -1（数字 i 与其在目标状态中位置的曼哈顿距离增加了 1），而 D(\textit{status}, \textit{next_status}) = 1，因此我们设计的启发函数是一致的。

我们在 A* 算法中使用该启发函数，即可得到最小的移动次数。

细节

我们可以预处理出任意两个位置的曼哈顿距离，位置的编号与方法一中的一致。距离矩阵如下：

\begin{bmatrix}
0 & 1 & 2 & 1 & 2 & 3 \
1 & 0 & 1 & 2 & 1 & 2 \
2 & 1 & 0 & 3 & 2 & 1 \
1 & 2 & 3 & 0 & 1 & 2 \
2 & 1 & 2 & 1 & 0 & 1 \
3 & 2 & 1 & 2 & 1 & 0
\end{bmatrix}

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
struct AStar {
    // 曼哈顿距离
    static constexpr array<array<int, 6>, 6> dist = {{
        {0, 1, 2, 1, 2, 3},
        {1, 0, 1, 2, 1, 2},
        {2, 1, 0, 3, 2, 1},
        {1, 2, 3, 0, 1, 2},
        {2, 1, 2, 1, 0, 1},
        {3, 2, 1, 2, 1, 0}
    }};

    // 计算启发函数
    static int getH(const string& status) {
        int ret = 0;
        for (int i = 0; i < 6; ++i) {
            if (status[i] != '0') {
                ret += dist[i][status[i] - '1'];
            }
        }
        return ret;
    };

    AStar(const string& status, int g): status_{status}, g_{g}, h_{getH(status)} {
        f_ = g_ + h_;
    }

    bool operator< (const AStar& that) const {
        return f_ > that.f_;
    }

    string status_;
    int f_, g_, h_;
};

class Solution {
private:
    vector<vector<int>> neighbors = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};;

public:
    int slidingPuzzle(vector<vector<int>>& board) {
        // 枚举 status 通过一次交换操作得到的状态
        auto get = [&](string& status) -> vector<string> {
            vector<string> ret;
            int x = status.find('0');
            for (int y: neighbors[x]) {
                swap(status[x], status[y]);
                ret.push_back(status);
                swap(status[x], status[y]);
            }
            return ret;
        };

        string initial;
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 3; ++j) {
                initial += char(board[i][j] + '0');
            }
        }
        if (initial == "123450") {
            return 0;
        }

        priority_queue<AStar> q;
        q.emplace(initial, 0);
        unordered_set<string> seen = {initial};

        while (!q.empty()) {
            AStar node = q.top();
            q.pop();
            for (auto&& next_status: get(node.status_)) {
                if (!seen.count(next_status)) {
                    if (next_status == "123450") {
                        return node.g_ + 1;
                    }
                    q.emplace(next_status, node.g_ + 1);
                    seen.insert(move(next_status));
                }
            }
        }

        return -1;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
class Solution {
    int[][] neighbors = {{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}};

    public int slidingPuzzle(int[][] board) {
        StringBuffer sb = new StringBuffer();
        for (int i = 0; i < 2; ++i) {
            for (int j = 0; j < 3; ++j) {
                sb.append(board[i][j]);
            }
        }
        String initial = sb.toString();
        if ("123450".equals(initial)) {
            return 0;
        }

        PriorityQueue<AStar> pq = new PriorityQueue<AStar>((a, b) -> a.f - b.f);
        pq.offer(new AStar(initial, 0));
        Set<String> seen = new HashSet<String>();
        seen.add(initial);

        while (!pq.isEmpty()) {
            AStar node = pq.poll();
            for (String nextStatus : get(node.status)) {
                if (!seen.contains(nextStatus)) {
                    if ("123450".equals(nextStatus)) {
                        return node.g + 1;
                    }
                    pq.offer(new AStar(nextStatus, node.g + 1));
                    seen.add(nextStatus);
                }
            }
        }

        return -1;
    }

    // 枚举 status 通过一次交换操作得到的状态
    public List<String> get(String status) {
        List<String> ret = new ArrayList<String>();
        char[] array = status.toCharArray();
        int x = status.indexOf('0');
        for (int y : neighbors[x]) {
            swap(array, x, y);
            ret.add(new String(array));
            swap(array, x, y);
        }
        return ret;
    }

    public void swap(char[] array, int x, int y) {
        char temp = array[x];
        array[x] = array[y];
        array[y] = temp;
    }
}

class AStar {
    // 曼哈顿距离
    public static int[][] dist = {
        {0, 1, 2, 1, 2, 3},
        {1, 0, 1, 2, 1, 2},
        {2, 1, 0, 3, 2, 1},
        {1, 2, 3, 0, 1, 2},
        {2, 1, 2, 1, 0, 1},
        {3, 2, 1, 2, 1, 0}
    };

    public String status;
    public int f, g, h;

    public AStar(String status, int g) {
        this.status = status;
        this.g = g;
        this.h = getH(status);
        this.f = this.g + this.h;
    }

    // 计算启发函数
    public static int getH(String status) {
        int ret = 0;
        for (int i = 0; i < 6; ++i) {
            if (status.charAt(i) != '0') {
                ret += dist[i][status.charAt(i) - '1'];
            }
        }
        return ret;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
class AStar:
    DIST = [
        [0, 1, 2, 1, 2, 3],
        [1, 0, 1, 2, 1, 2],
        [2, 1, 0, 3, 2, 1],
        [1, 2, 3, 0, 1, 2],
        [2, 1, 2, 1, 0, 1],
        [3, 2, 1, 2, 1, 0],
    ]

    # 计算启发函数
    @staticmethod
    def getH(status: str) -> int:
        ret = 0
        for i in range(6):
            if status[i] != "0":
                ret += AStar.DIST[i][int(status[i]) - 1]
        return ret

    def __init__(self, status: str, g: str) -> None:
        self.status = status
        self.g = g
        self.h = AStar.getH(status)
        self.f = self.g + self.h
    
    def __lt__(self, other: "AStar") -> bool:
        return self.f < other.f

class Solution:
    NEIGHBORS = [[1, 3], [0, 2, 4], [1, 5], [0, 4], [1, 3, 5], [2, 4]]

    def slidingPuzzle(self, board: List[List[int]]) -> int:
        # 枚举 status 通过一次交换操作得到的状态
        def get(status: str) -> Generator[str, None, None]:
            s = list(status)
            x = s.index("0")
            for y in Solution.NEIGHBORS[x]:
                s[x], s[y] = s[y], s[x]
                yield "".join(s)
                s[x], s[y] = s[y], s[x]

        initial = "".join(str(num) for num in sum(board, []))
        if initial == "123450":
            return 0

        q = [AStar(initial, 0)]
        seen = {initial}
        while q:
            node = heapq.heappop(q)
            for next_status in get(node.status):
                if next_status not in seen:
                    if next_status == "123450":
                        return node.g + 1
                    heapq.heappush(q, AStar(next_status, node.g + 1))
                    seen.add(next_status)
        
        return -1
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
type astar struct {
    g, h   int
    status string
}
type hp []astar

func (h hp) Len() int            { return len(h) }
func (h hp) Less(i, j int) bool  { return h[i].g+h[i].h < h[j].g+h[j].h }
func (h hp) Swap(i, j int)       { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(astar)) }
func (h *hp) Pop() interface{}   { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

// 曼哈顿距离
var dist = [6][6]int{
    {0, 1, 2, 1, 2, 3},
    {1, 0, 1, 2, 1, 2},
    {2, 1, 0, 3, 2, 1},
    {1, 2, 3, 0, 1, 2},
    {2, 1, 2, 1, 0, 1},
    {3, 2, 1, 2, 1, 0},
}

// 计算启发函数
func getH(status string) (ret int) {
    for i, ch := range status {
        if ch != '0' {
            ret += dist[i][ch-'1']
        }
    }
    return
}

var neighbors = [6][]int{{1, 3}, {0, 2, 4}, {1, 5}, {0, 4}, {1, 3, 5}, {2, 4}}

func slidingPuzzle(board [][]int) int {
    const target = "123450"

    s := make([]byte, 0, 6)
    for _, r := range board {
        for _, v := range r {
            s = append(s, '0'+byte(v))
        }
    }
    start := string(s)
    if start == target {
        return 0
    }

    // 枚举 status 通过一次交换操作得到的状态
    get := func(status string) (ret []string) {
        s := []byte(status)
        x := strings.Index(status, "0")
        for _, y := range neighbors[x] {
            s[x], s[y] = s[y], s[x]
            ret = append(ret, string(s))
            s[x], s[y] = s[y], s[x]
        }
        return
    }

    type pair struct {
        status string
        step   int
    }
    h := hp{{0, getH(start), start}}
    seen := map[string]bool{start: true}
    for len(h) > 0 {
        node := heap.Pop(&h).(astar)
        for _, nxt := range get(node.status) {
            if !seen[nxt] {
                if nxt == target {
                    return node.g + 1
                }
                seen[nxt] = true
                heap.Push(&h, astar{node.g + 1, getH(nxt), nxt})
            }
        }
    }
    return -1
}

复杂度分析

启发式搜索不讨论时空复杂度。

 Comments
On this page
0773-滑动谜题