0803-打砖块

有一个 m x n 的二元网格 grid ，其中 1 表示砖块，0 表示空白。砖块 稳定 （不会掉落）的前提是：

• 一块砖直接连接到网格的顶部，或者
• 至少有一块相邻（4 个方向之一）砖块 稳定 不会掉落时

给你一个数组 hits ，这是需要依次消除砖块的位置。每当消除 hits[i] = (rowi, coli)
位置上的砖块时，对应位置的砖块（若存在）会消失，然后其他的砖块可能因为这一消除操作而 掉落 。一旦砖块掉落，它会 立即 从网格 grid
中消失（即，它不会落在其他稳定的砖块上）。

返回一个数组 result ，其中 result[i] 表示第 i 次消除操作对应掉落的砖块数目。

注意 ，消除可能指向是没有砖块的空白位置，如果发生这种情况，则没有砖块掉落。

示例 1：

**输入：** grid = [[1,0,0,0],[1,1,1,0]], hits = [[1,0]]
**输出：** [2]
**解释：** 网格开始为：
[[1,0,0,0]，
 [ **1** ,1,1,0]]
消除 (1,0) 处加粗的砖块，得到网格：
[[1,0,0,0]
 [0, **1** , **1** ,0]]
两个加粗的砖不再稳定，因为它们不再与顶部相连，也不再与另一个稳定的砖相邻，因此它们将掉落。得到网格：
[[1,0,0,0],
 [0,0,0,0]]
因此，结果为 [2] 。

示例 2：

**输入：** grid = [[1,0,0,0],[1,1,0,0]], hits = [[1,1],[1,0]]
**输出：** [0,0]
**解释：** 网格开始为：
[[1,0,0,0],
 [1, **1** ,0,0]]
消除 (1,1) 处加粗的砖块，得到网格：
[[1,0,0,0],
 [1,0,0,0]]
剩下的砖都很稳定，所以不会掉落。网格保持不变：
[[1,0,0,0], 
 [ **1** ,0,0,0]]
接下来消除 (1,0) 处加粗的砖块，得到网格：
[[1,0,0,0],
 [0,0,0,0]]
剩下的砖块仍然是稳定的，所以不会有砖块掉落。
因此，结果为 [0,0] 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• grid[i][j] 为 0 或 1
• 1 <= hits.length <= 4 * 104
• hits[i].length == 2
• 0 <= xi <= m - 1
• 0 <= yi <= n - 1
• 所有 (xi, yi) 互不相同

📺 视频讲解

力扣君温馨小贴士：觉得视频时间长的扣友，可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看。

📖 文字解析

阅读提示：我们在文字描述中给出的 4 个图，覆盖了这个问题的几种特殊情况，包括了一般情况和特殊情况，还有不可能出现的情况。

1. 解释题意

首先，题解题意很重要。不会掉落的「砖块」需要满足两个条件：

• 「砖块」位于下标为 0 的行；
• 与下标为 0 的行的砖块在上、下、左、右 4 个方向上相连。

题目问按照数组 hits 中击落砖块的顺序，每一次有多少个砖块因为这个被击碎的砖块而消失。解题的时候须要注意以下两个条件（原因最后说）：

• 一旦砖块掉落，它会立即从网格中消失（它不会落在其他稳定的砖块上）；
• 所有的 (x_i, y_i) 互不相同。

2. 如何计算每次击碎砖块而消失的砖块的数量（关注「与屋顶相连的砖块的总数变化」）

和顶部相连的砖块不会掉落，击碎了一个砖块以后，可能会使得其它与 被击碎砖块 连接的砖块不再与顶部相连，然后它们消失。

「击碎砖块之前」与「击碎砖块之后」与 屋顶 相连的砖块数的差值，再减 1 就是因为这一次操作而消失的砖块数。如下图所示：

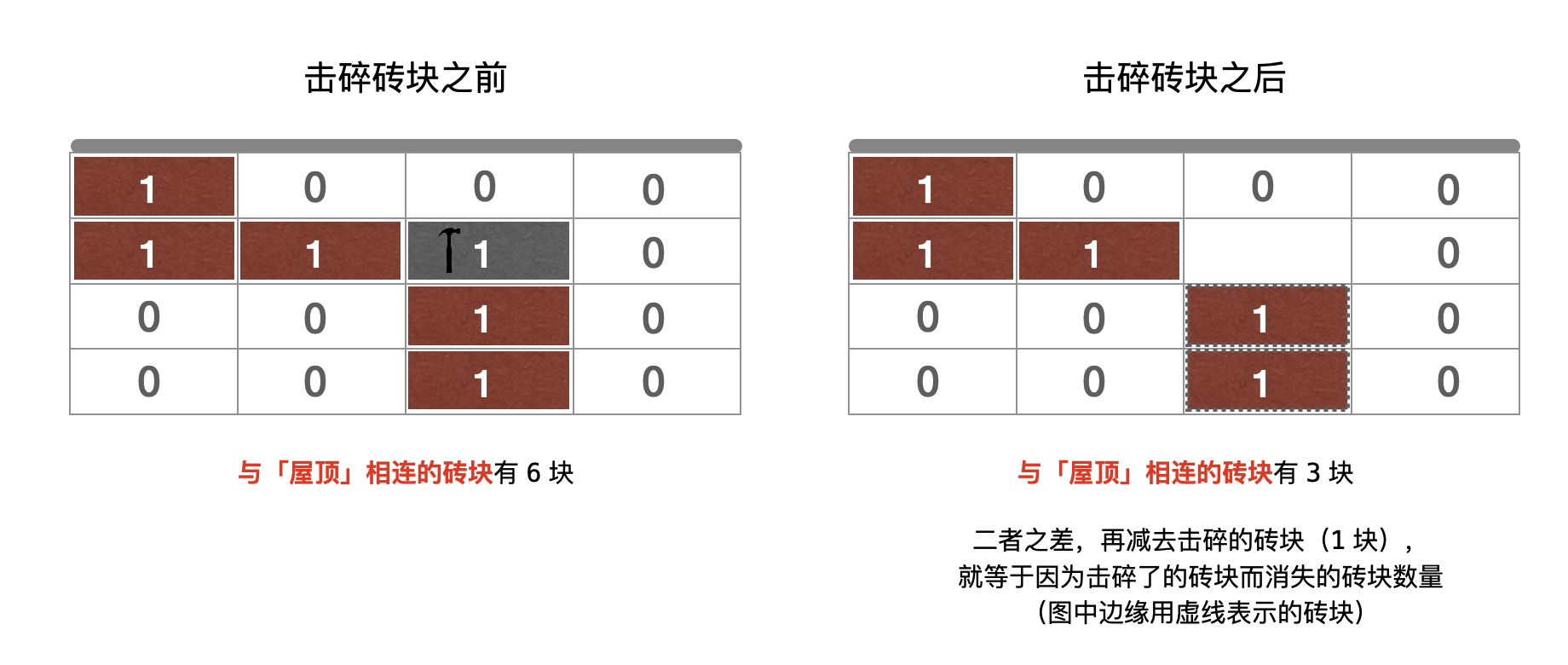
3. 如何想到并查集

• 当前问题是一个图的连通性问题，砖块和砖块如果在 4 个方向上相邻，表示这两个砖块上有一条边。砖块的相邻关系而产生的连接关系具有传递性；
• 第 0 行的砖块连接着「屋顶」；
• 击碎了一个砖块以后，可能会使得其它与「被击碎砖块」 连接 的砖块不再与顶部相连，然后它们消失；
• 题目只问结果，没有问具体连接的情况；
• 连通的砖块个数是我们所关心的，「并查集」内部可以维护「以当前结点为根结点的子树的结点总数」。

4. 如何使用并查集

• 消除一个砖块的效果是：一个连通分量被分成了两个连通分量；
• 并查集的作用是：把两个连通分量合并成一个连通分量。

提示我们这个问题需要 反向 思考。即考虑：补上被击碎的砖块以后，有多少个砖块因为这个补上的这个砖块而与屋顶的砖块相连。每一次击碎一个砖块，因击碎砖块而消失的砖块只会越来越少。因此可以按照数组 hits 的顺序 逆序地 把这些砖块依次补上。如图所示：

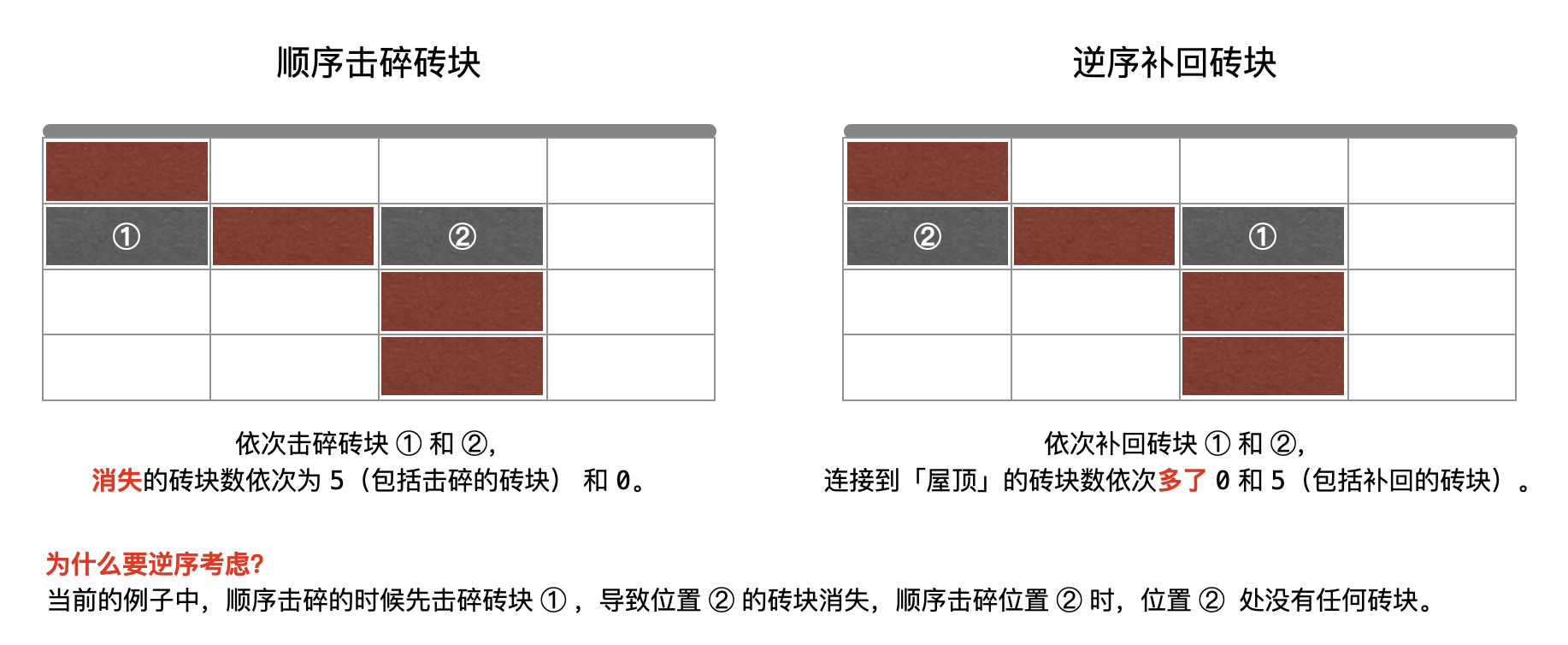
当最后一块砖块补上的时候，就恰好可以恢复成刚开始的时候整个二维表格的样子。

5. 解题步骤

• 根据数组 hits，将输入的表格 grid 里的对应位置全部设置为 0 ，这是因为我们要逆序补全出整个初始化的时候二维表格的砖块；
• 从最后一个击碎的砖块开始，计算补上这个被击碎的砖块的时候，有多少个砖块因为这个补上的砖块而与屋顶相连，这个数目就是按照题目中的描述，击碎砖块以后掉落的砖块的数量。

下面我们介绍实现细节。

6. 实现细节

• 在并查集中设置一个特殊的结点，表示「屋顶」；
• 逆序补回的时候，由于补回，增加的连接到「屋顶」的砖块数应该这样算：res[i] = Math.max(0, current - origin - 1); （current 和 origin 的含义请见代码）。因为有可能补回一个砖块前后，连接到「屋顶」的砖块总数没有变化，如下图所示：

{:width=500}

参考代码：

力扣君温馨小贴士：为了保证语义和层次清晰，我们加入了注释和空行，所以代码看起来有点长，但主要的逻辑就 3 步。我们建议大家先理解逻辑的先后顺序，尝试自己实现，然后再看代码的细节。

[]

public class Solution {

    private int rows;
    private int cols;

    public static final int[][] DIRECTIONS = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}};

    public int[] hitBricks(int[][] grid, int[][] hits) {
        this.rows = grid.length;
        this.cols = grid[0].length;

        // 第 1 步：把 grid 中的砖头全部击碎，通常算法问题不能修改输入数据，这一步非必需，可以认为是一种答题规范
        int[][] copy = new int[rows][cols];
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                copy[i][j] = grid[i][j];
            }
        }

        // 把 copy 中的砖头全部击碎
        for (int[] hit : hits) {
            copy[hit[0]][hit[1]] = 0;
        }

        // 第 2 步：建图，把砖块和砖块的连接关系输入并查集，size 表示二维网格的大小，也表示虚拟的「屋顶」在并查集中的编号
        int size = rows * cols;
        UnionFind unionFind = new UnionFind(size + 1);

        // 将下标为 0 的这一行的砖块与「屋顶」相连
        for (int j = 0; j < cols; j++) {
            if (copy[0][j] == 1) {
                unionFind.union(j, size);
            }
        }

        // 其余网格，如果是砖块向上、向左看一下，如果也是砖块，在并查集中进行合并
        for (int i = 1; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (copy[i][j] == 1) {
                    // 如果上方也是砖块
                    if (copy[i - 1][j] == 1) {
                        unionFind.union(getIndex(i - 1, j), getIndex(i, j));
                    }
                    // 如果左边也是砖块
                    if (j > 0 && copy[i][j - 1] == 1) {
                        unionFind.union(getIndex(i, j - 1), getIndex(i, j));
                    }
                }
            }
        }

        // 第 3 步：按照 hits 的逆序，在 copy 中补回砖块，把每一次因为补回砖块而与屋顶相连的砖块的增量记录到 res 数组中
        int hitsLen = hits.length;
        int[] res = new int[hitsLen];
        for (int i = hitsLen - 1; i >= 0; i--) {
            int x = hits[i][0];
            int y = hits[i][1];

            // 注意：这里不能用 copy，语义上表示，如果原来在 grid 中，这一块是空白，这一步不会产生任何砖块掉落
            // 逆向补回的时候，与屋顶相连的砖块数量也肯定不会增加
            if (grid[x][y] == 0) {
                continue;
            }

            // 补回之前与屋顶相连的砖块数
            int origin = unionFind.getSize(size);

            // 注意：如果补回的这个结点在第 1 行，要告诉并查集它与屋顶相连（逻辑同第 2 步）
            if (x == 0) {
                unionFind.union(y, size);
            }

            // 在 4 个方向上看一下，如果相邻的 4 个方向有砖块，合并它们
            for (int[] direction : DIRECTIONS) {
                int newX = x + direction[0];
                int newY = y + direction[1];

                if (inArea(newX, newY) && copy[newX][newY] == 1) {
                    unionFind.union(getIndex(x, y), getIndex(newX, newY));
                }
            }

            // 补回之后与屋顶相连的砖块数
            int current = unionFind.getSize(size);
            // 减去的 1 是逆向补回的砖块（正向移除的砖块），与 0 比较大小，是因为存在一种情况，添加当前砖块，不会使得与屋顶连接的砖块数更多
            res[i] = Math.max(0, current - origin - 1);

            // 真正补上这个砖块
            copy[x][y] = 1;
        }
        return res;
    }

    /**
     * 输入坐标在二维网格中是否越界
     *
     * @param x
     * @param y
     * @return
     */
    private boolean inArea(int x, int y) {
        return x >= 0 && x < rows && y >= 0 && y < cols;
    }

    /**
     * 二维坐标转换为一维坐标
     *
     * @param x
     * @param y
     * @return
     */
    private int getIndex(int x, int y) {
        return x * cols + y;
    }

    private class UnionFind {

        /**
         * 当前结点的父亲结点
         */
        private int[] parent;
        /**
         * 以当前结点为根结点的子树的结点总数
         */
        private int[] size;

        public UnionFind(int n) {
            parent = new int[n];
            size = new int[n];
            for (int i = 0; i < n; i++) {
                parent[i] = i;
                size[i] = 1;
            }
        }

        /**
         * 路径压缩，只要求每个不相交集合的「根结点」的子树包含的结点总数数值正确即可，因此在路径压缩的过程中不用维护数组 size
         *
         * @param x
         * @return
         */
        public int find(int x) {
            if (x != parent[x]) {
                parent[x] = find(parent[x]);
            }
            return parent[x];
        }

        public void union(int x, int y) {
            int rootX = find(x);
            int rootY = find(y);

            if (rootX == rootY) {
                return;
            }
            parent[rootX] = rootY;
            // 在合并的时候维护数组 size
            size[rootY] += size[rootX];
        }

        /**
         * @param x
         * @return x 在并查集的根结点的子树包含的结点总数
         */
        public int getSize(int x) {
            int root = find(x);
            return size[root];
        }
    }
}

复杂度分析

• 时间复杂度：O((N + rows \cdot cols) \cdot \log(rows \cdot cols))，其中 N 为数组 hits 的长度，rows 和 cols 分别为矩阵的行数和列数，只使用了路径压缩，并查集的单次操作的时间复杂度为 O(\log(rows \cdot cols))；

• 空间复杂度：O(rows \cdot cols)。

7. 解释开篇说的两个条件

• 条件 1：一旦砖块掉落，它会立即从网格中消失（它不会落在其他稳定的砖块上），意思是下面的这种情况不会出现。

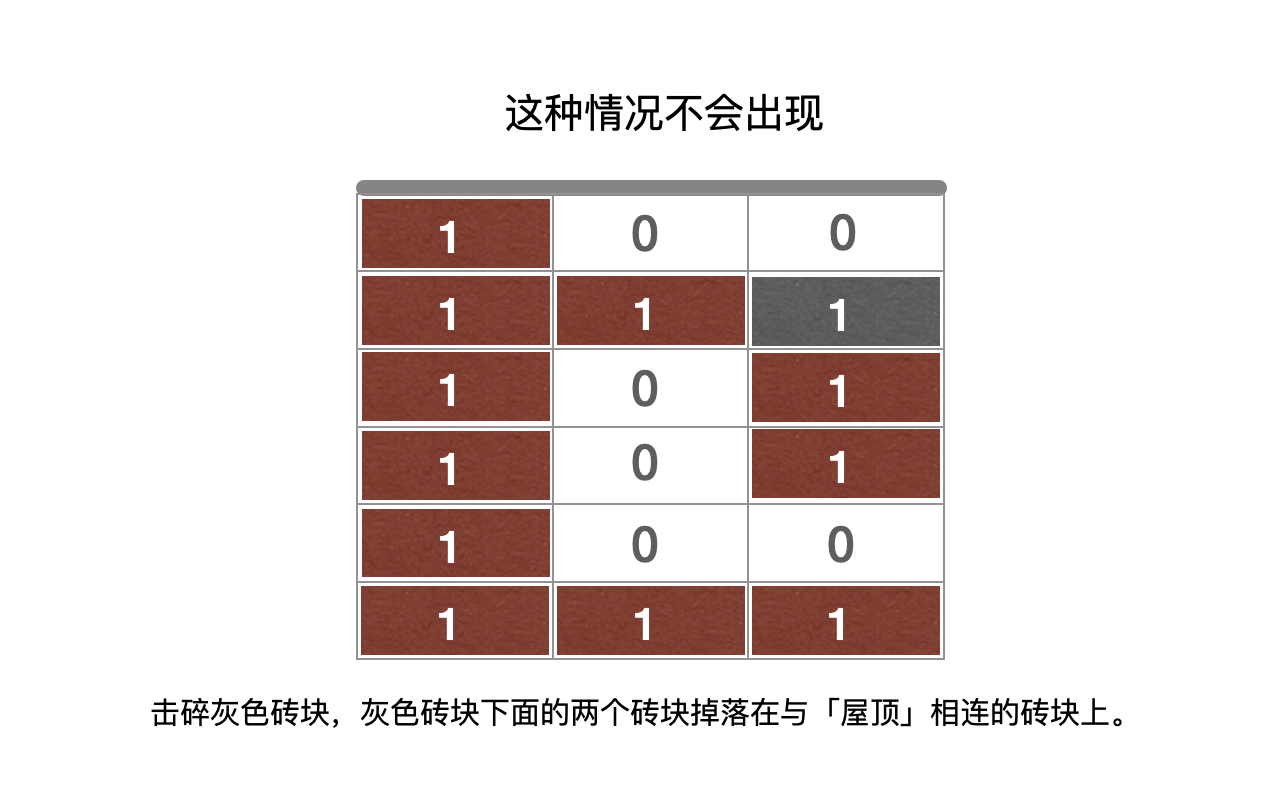{:width=500}

• 条件 2：所有的 (x_i, y_i) 互不相同。如果 hits 数组里有相同的结点，逆序把这些砖块补充回去以后，有可能出现以下情况：
  • 不能拼接出初始化的时候整个二维表格；
  • 同一个位置的砖块敲击两次，逆序求解的时候，第 1 次补回去的时候，把结果记录 res[i]，第 2 次由于敲了同一个位置，在之前的 res[i] 这一步操作其实是无效的，应该恢复成 0。

如果没有这两个条件，求解这个问题会变得复杂。大家在做题的时候一定要注意题目中的限制，以免漏看条件或者加强了题目的条件。

---

这种逆向去考虑一个问题的思路其实在「力扣」上并不少见，感兴趣的朋友可以复习一下我们在打卡题中曾经做过的：174. 地下城游戏 和 312. 戳气球 。