0812-最大三角形面积

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:45:43 2023-09-13 16:45:43 Updated    

给你一个由 X-Y 平面上的点组成的数组 points ，其中 points[i] = [xi, yi]
。从其中取任意三个不同的点组成三角形，返回能组成的最大三角形的面积。与真实值误差在 10-5 内的答案将会视为正确答案 。

示例 1：

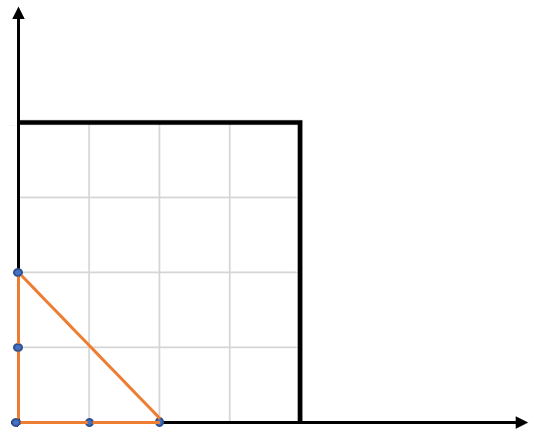
**输入：** points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
**输出：** 2.00000
**解释：** 输入中的 5 个点如上图所示，红色的三角形面积最大。

示例 2：

**输入：** points = [[1,0],[0,0],[0,1]]
**输出：** 0.50000

提示：

  • 3 <= points.length <= 50
  • -50 <= xi, yi <= 50
  • 给出的所有点 互不相同

方法一：枚举

思路与算法

关于求解三角形面积的公式可以参考百度百科「三角形面积公式 」。

我们可以枚举所有的三角形，然后计算三角形的面积并找出最大的三角形面积。设三角形三个顶点的坐标为 (x_1, y_1)、(x_2, y_2) 和 (x_3, y_3)，则三角形面积 S 可以用行列式的绝对值表示：

S = 1/2} \left| \begin{vmatrix} x_1 & y_1 & 1 \ x_2 & y_2 & 1 \ x_3 & y_3 &1 \end{vmatrix} \right| = 1/2} \lvert x_1 y_2 + x_2 y_3 + x_3 y_1 - x_1 y_3 - x_2 y_1 - x_3 y_2 \rvert

代码

[sol1-Python3]
1
2
3
4
5
class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        def triangleArea(x1: int, y1: int, x2: int, y2: int, x3: int, y3: int) -> float:
            return abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2) / 2
        return max(triangleArea(x1, y1, x2, y2, x3, y3) for (x1, y1), (x2, y2), (x3, y3) in combinations(points, 3))
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    double triangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
        return 0.5 * abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
    }

    double largestTriangleArea(vector<vector<int>> & points) {
        int n = points.size();
        double ret = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    ret = max(ret, triangleArea(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]));
                }
            }
        }
        return ret;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public double largestTriangleArea(int[][] points) {
        int n = points.length;
        double ret = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    ret = Math.max(ret, triangleArea(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]));
                }
            }
        }
        return ret;
    }

    public double triangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
        return 0.5 * Math.abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public class Solution {
    public double LargestTriangleArea(int[][] points) {
        int n = points.Length;
        double ret = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {
                for (int k = j + 1; k < n; k++) {
                    ret = Math.Max(ret, TriangleArea(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]));
                }
            }
        }
        return ret;
    }

    public double TriangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
        return 0.5 * Math.Abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
    }
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
static inline double max(double a, double b) {
    return a > b ? a : b;
}

double triangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
    return 0.5 * abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
}

double largestTriangleArea(int** points, int pointsSize, int* pointsColSize){
    double ret = 0.0;
    for (int i = 0; i < pointsSize; i++) {
        for (int j = i + 1; j < pointsSize; j++) {
            for (int k = j + 1; k < pointsSize; k++) {
                double area = triangleArea(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]);
                ret = max(ret, area);
            }
        }
    }
    return ret;
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
var largestTriangleArea = function(points) {
    const n = points.length;
    let ret = 0.0;
    for (let i = 0; i < n; i++) {
        for (let j = i + 1; j < n; j++) {
            for (let k = j + 1; k < n; k++) {
                ret = Math.max(ret, triangleArea(points[i][0], points[i][1], points[j][0], points[j][1], points[k][0], points[k][1]));
            }
        }
    }
    return ret;
};

const triangleArea = (x1, y1, x2, y2, x3, y3) => {
    return 0.5 * Math.abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
func triangleArea(x1, y1, x2, y2, x3, y3 int) float64 {
    return math.Abs(float64(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2)) / 2
}

func largestTriangleArea(points [][]int) (ans float64) {
    for i, p := range points {
        for j, q := range points[:i] {
            for _, r := range points[:j] {
                ans = math.Max(ans, triangleArea(p[0], p[1], q[0], q[1], r[0], r[1]))
            }
        }
    }
    return
}

复杂度分析

  • 时间复杂度：O(n^3)，其中 n 是数组 points 的长度。三重循环需要 O(n^3)。

  • 空间复杂度：O(1)。

方法二：凸包

思路与算法

我们先使用 Andrew 算法求出所有点对应的凸包 convexHull，参考官方题解「587. 安装栅栏 」的凸包算法。

如果三角形的某一点不在凸包上，我们以其余两点的边为底，那么我们总可以在凸包上找到一个点，使得该点到此边的高大于原来的点到此边的高，因此面积最大的三角形的三个点都在凸包上。

在凸包 convexHull 上枚举三角形，先枚举点 i，然后枚举点 j，最后枚举点 k，其中 i \lt j \lt k。

在固定点 i 和 j 后，三角形的面积与 k 的关系是一个凸曲线，因此三角形只在 k 为极点时面积最大。在固定点 i 时，该极点在随点 j 增大而增大，因此在搜索极点只需要从上次的极点位置开始搜索。

所以我们不需要枚举点 k，只需要搜索点 i 和 j 对应的极点，然后求解三角形面积。返回最大的三角形面积。

代码

[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution:
    def getConvexHull(self, points: List[List[int]]) -> List[List[int]]:
        def cross(p: List[int], q: List[int], r: List[int]) -> int:
            return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0])

        n = len(points)
        if n < 4:
            return points

        # 按照 x 从小到大排序，如果 x 相同，则按照 y 从小到大排序
        points.sort()

        hull = []
        # 求凸包的下半部分
        for i, p in enumerate(points):
            while len(hull) > 1 and cross(hull[-2], hull[-1], p) <= 0:
                hull.pop()
            hull.append(p)
        # 求凸包的上半部分
        m = len(hull)
        for i in range(n - 2, -1, -1):
            while len(hull) > m and cross(hull[-2], hull[-1], points[i]) <= 0:
                hull.pop()
            hull.append(points[i])
        hull.pop()  # hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0]
        return hull

    def largestTriangleArea(self, points: List[List[int]]) -> float:
        def triangleArea(x1: int, y1: int, x2: int, y2: int, x3: int, y3: int) -> float:
            return abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2) / 2

        convexHull = self.getConvexHull(points)
        ans, n = 0, len(convexHull)
        for i, p in enumerate(convexHull):
            k = i + 2
            for j in range(i + 1, n - 1):
                q = convexHull[j]
                while k + 1 < n:
                    curArea = triangleArea(p[0], p[1], q[0], q[1], convexHull[k][0], convexHull[k][1])
                    nextArea = triangleArea(p[0], p[1], q[0], q[1], convexHull[k + 1][0], convexHull[k + 1][1])
                    if curArea >= nextArea:
                        break
                    k += 1
                ans = max(ans, triangleArea(p[0], p[1], q[0], q[1], convexHull[k][0], convexHull[k][1]))
        return ans
[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
class Solution {
private:
    int cross(const vector<int> & p, const vector<int> & q, const vector<int> & r) {
        return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
    }

    vector<vector<int>> getConvexHull(vector<vector<int>>& points) {
        int n = points.size();
        if (n < 4) {
            return points;
        }
        /* 按照 x 大小进行排序，如果 x 相同，则按照 y 的大小进行排序 */
        sort(points.begin(), points.end(), [](const vector<int> & a, const vector<int> & b) {
            if (a[0] == b[0]) {
                return a[1] < b[1];
            }
            return a[0] < b[0];
        });
        vector<vector<int>> hull;
        /* 求出凸包的下半部分 */
        for (int i = 0; i < n; i++) {
            while (hull.size() > 1 && cross(hull[hull.size() - 2], hull.back(), points[i]) <= 0) {
                hull.pop_back();
            }
            hull.emplace_back(points[i]);
        }
        int m = hull.size();
        /* 求出凸包的上半部分 */
        for (int i = n - 2; i >= 0; i--) {
            while (hull.size() > m && cross(hull[hull.size() - 2], hull.back(), points[i]) <= 0) {
                hull.pop_back();
            }
            hull.emplace_back(points[i]);
        }
        /* hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0] */
        hull.pop_back();
        return hull;
    }

    double triangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
        return 0.5 * abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
    }

public:
    double largestTriangleArea(vector<vector<int>> & points) {
        auto convexHull = getConvexHull(points);
        int n = convexHull.size();
        double ret = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1, k = i + 2; j + 1 < n; j++) {
                while (k + 1 < n) {
                    double curArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                    double nextArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k + 1][0], convexHull[k + 1][1]);
                    if (curArea >= nextArea) {
                        break;
                    }
                    k++;
                }
                double area = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                ret = max(ret, area);
            }
        }
        return ret;
    }
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
class Solution {
    public double largestTriangleArea(int[][] points) {
        int[][] convexHull = getConvexHull(points);
        int n = convexHull.length;
        double ret = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1, k = i + 2; j + 1 < n; j++) {
                while (k + 1 < n) {
                    double curArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                    double nextArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k + 1][0], convexHull[k + 1][1]);
                    if (curArea >= nextArea) {
                        break;
                    }
                    k++;
                }
                double area = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                ret = Math.max(ret, area);
            }
        }
        return ret;
    }

    public int[][] getConvexHull(int[][] points) {
        int n = points.length;
        if (n < 4) {
            return points;
        }
        /* 按照 x 大小进行排序，如果 x 相同，则按照 y 的大小进行排序 */
        Arrays.sort(points, (a, b) -> {
            if (a[0] == b[0]) {
                return a[1] - b[1];
            }
            return a[0] - b[0];
        });
        List<int[]> hull = new ArrayList<int[]>();
        /* 求出凸包的下半部分 */
        for (int i = 0; i < n; i++) {
            while (hull.size() > 1 && cross(hull.get(hull.size() - 2), hull.get(hull.size() - 1), points[i]) <= 0) {
                hull.remove(hull.size() - 1);
            }
            hull.add(points[i]);
        }
        int m = hull.size();
        /* 求出凸包的上半部分 */
        for (int i = n - 2; i >= 0; i--) {
            while (hull.size() > m && cross(hull.get(hull.size() - 2), hull.get(hull.size() - 1), points[i]) <= 0) {
                hull.remove(hull.size() - 1);
            }
            hull.add(points[i]);
        }
        /* hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0] */
        hull.remove(hull.size() - 1);
        m = hull.size();
        int[][] hullArr = new int[m][];
        for (int i = 0; i < m; i++) {
            hullArr[i] = hull.get(i);
        }
        return hullArr;
    }

    public double triangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
        return 0.5 * Math.abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
    }

    public int cross(int[] p, int[] q, int[] r) {
        return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
    }
}
[sol2-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
public class Solution {
    public double LargestTriangleArea(int[][] points) {
        int[][] convexHull = getConvexHull(points);
        int n = convexHull.Length;
        double ret = 0.0;
        for (int i = 0; i < n; i++) {
            for (int j = i + 1, k = i + 2; j + 1 < n; j++) {
                while (k + 1 < n) {
                    double curArea = TriangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                    double nextArea = TriangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k + 1][0], convexHull[k + 1][1]);
                    if (curArea >= nextArea) {
                        break;
                    }
                    k++;
                }
                double area = TriangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                ret = Math.Max(ret, area);
            }
        }
        return ret;
    }

    public int[][] getConvexHull(int[][] points) {
        int n = points.Length;
        if (n < 4) {
            return points;
        }
        /* 按照 x 大小进行排序，如果 x 相同，则按照 y 的大小进行排序 */
        Array.Sort(points, (a, b) => {
            if (a[0] == b[0]) {
                return a[1] - b[1];
            }
            return a[0] - b[0];
        });
        IList<int[]> hull = new List<int[]>();
        /* 求出凸包的下半部分 */
        for (int i = 0; i < n; i++) {
            while (hull.Count > 1 && Cross(hull[hull.Count - 2], hull[hull.Count - 1], points[i]) <= 0) {
                hull.RemoveAt(hull.Count - 1);
            }
            hull.Add(points[i]);
        }
        int m = hull.Count;
        /* 求出凸包的上半部分 */
        for (int i = n - 2; i >= 0; i--) {
            while (hull.Count > m && Cross(hull[hull.Count - 2], hull[hull.Count - 1], points[i]) <= 0) {
                hull.RemoveAt(hull.Count - 1);
            }
            hull.Add(points[i]);
        }
        /* hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0] */
        hull.RemoveAt(hull.Count - 1);
        m = hull.Count;
        int[][] hullArr = new int[m][];
        for (int i = 0; i < m; i++) {
            hullArr[i] = hull[i];
        }
        return hullArr;
    }

    public double TriangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
        return 0.5 * Math.Abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
    }

    public int Cross(int[] p, int[] q, int[] r) {
        return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
    }
}
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91

static int cross(const int * p, const int * q, const int * r) {
    return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
}

static int cmp(const void * pa, const void * pb) {
    int *a = *((int **)pa);
    int *b = *((int **)pb);
    if (a[0] == b[0]) {
        return a[1] - b[1];
    }
    return a[0] - b[0];
}

static int** getConvexHull(int** points, int pointsSize, int* pointsColSize, int* returnSize) {
    int **res = (int **)malloc(sizeof(int *) * pointsSize);
    int pos = 0;
    if (pointsSize < 4) {
        for (int i = 0; i < pointsSize; i++) {
            res[i] = (int *)malloc(sizeof(int) * 2);
            res[i][0] = points[i][0];
            res[i][1] = points[i][1];
        }
        *returnSize = pointsSize;
        return res;
    }
    
    qsort(points, pointsSize, sizeof(int *), cmp);
    int * hull = (int *)malloc(sizeof(int) * (pointsSize + 1));
    int * used = (int *)malloc(sizeof(int) * pointsSize);
    /* hull[0] 需要入栈两次 */
    hull[pos++] = 0;
    /* 求出凸包的下半部分 */
    for (int i = 1; i < pointsSize; i++) {
        while (pos > 1 && cross(points[hull[pos - 2]], points[hull[pos - 1]], points[i]) <= 0) {
            pos--;
        }
        hull[pos++] = i;
    }
    int m = pos;
    /* 求出凸包的上半部分 */
    for (int i = pointsSize - 2; i >= 0; i--) {
        while (pos > m && cross(points[hull[pos - 2]], points[hull[pos - 1]], points[i]) <= 0) {
            pos--;
        }
        hull[pos++] = i;
    }
    /* hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0] */
    pos--;
    *returnSize = pos;
    for (int i = 0; i < pos; i++) {
        res[i] = (int *)malloc(sizeof(int) * 2);
        memcpy(res[i], points[hull[i]], sizeof(int) * 2);
    }
    free(used);
    free(hull);
    return res;
}

static inline double max(double a, double b) {
    return a > b ? a : b;
}

double triangleArea(int x1, int y1, int x2, int y2, int x3, int y3) {
    return 0.5 * abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
}

double largestTriangleArea(int** points, int pointsSize, int* pointsColSize){
    int hullSize = 0;
    int **convexHull = getConvexHull(points, pointsSize, pointsColSize, &hullSize);
    double ret = 0.0;
    for (int i = 0; i < hullSize; i++) {
        for (int j = i + 1, k = i + 2; j + 1 < hullSize; j++) {
            while (k + 1 < hullSize) {
                double curArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                double nextArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k + 1][0], convexHull[k + 1][1]);
                if (curArea >= nextArea) {
                    break;
                }
                k++;
            }
            double area = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
            ret = max(ret, area);
        }
    }
    for (int i = 0; i < hullSize; i++) {
        free(convexHull[i]);
    }
    free(convexHull);
    return ret;
}
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
func cross(p, q, r []int) int {
    return (q[0]-p[0])*(r[1]-q[1]) - (q[1]-p[1])*(r[0]-q[0])
}

func getConvexHull(points [][]int) [][]int {
    n := len(points)
    if n < 4 {
        return points
    }

    // 按照 x 从小到大排序，如果 x 相同，则按照 y 从小到大排序
    sort.Slice(points, func(i, j int) bool { a, b := points[i], points[j]; return a[0] < b[0] || a[0] == b[0] && a[1] < b[1] })

    hull := [][]int{}
    // 求凸包的下半部分
    for _, p := range points {
        for len(hull) > 1 && cross(hull[len(hull)-2], hull[len(hull)-1], p) <= 0 {
            hull = hull[:len(hull)-1]
        }
        hull = append(hull, p)
    }
    // 求凸包的上半部分
    m := len(hull)
    for i := n - 1; i >= 0; i-- {
        for len(hull) > m && cross(hull[len(hull)-2], hull[len(hull)-1], points[i]) <= 0 {
            hull = hull[:len(hull)-1]
        }
        hull = append(hull, points[i])
    }
    // hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0]
    return hull[:len(hull)-1]
}

func triangleArea(x1, y1, x2, y2, x3, y3 int) float64 {
    return math.Abs(float64(x1*y2+x2*y3+x3*y1-x1*y3-x2*y1-x3*y2)) / 2
}

func largestTriangleArea(points [][]int) (ans float64) {
    convexHull := getConvexHull(points)
    n := len(convexHull)
    for i, p := range convexHull {
        for j, k := i+1, i+2; j+1 < n; j++ {
            q := convexHull[j]
            for ; k+1 < n; k++ {
                curArea := triangleArea(p[0], p[1], q[0], q[1], convexHull[k][0], convexHull[k][1])
                nextArea := triangleArea(p[0], p[1], q[0], q[1], convexHull[k+1][0], convexHull[k+1][1])
                if curArea >= nextArea {
                    break
                }
            }
            ans = math.Max(ans, triangleArea(p[0], p[1], q[0], q[1], convexHull[k][0], convexHull[k][1]))
        }
    }
    return
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
var largestTriangleArea = function(points) {
    const convexHull = getConvexHull(points);
    const n = convexHull.length;
    let ret = 0.0;
    for (let i = 0; i < n; i++) {
        for (let j = i + 1, k = i + 2; j + 1 < n; j++) {
            while (k + 1 < n) {
                const curArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
                const nextArea = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k + 1][0], convexHull[k + 1][1]);
                if (curArea >= nextArea) {
                    break;
                }
                k++;
            }
            const area = triangleArea(convexHull[i][0], convexHull[i][1], convexHull[j][0], convexHull[j][1], convexHull[k][0], convexHull[k][1]);
            ret = Math.max(ret, area);
        }
    }
    return ret;
}

const getConvexHull = (points) => {
    const n = points.length;
    if (n < 4) {
        return points;
    }
    /* 按照 x 大小进行排序，如果 x 相同，则按照 y 的大小进行排序 */
    points.sort((a, b) => {
        if (a[0] === b[0]) {
            return a[1] - b[1];
        }
        return a[0] - b[0];
    });
    const hull = [];
    /* 求出凸包的下半部分 */
    for (let i = 0; i < n; i++) {
        while (hull.length > 1 && cross(hull[hull.length - 2], hull[hull.length - 1], points[i]) <= 0) {
            hull.pop();
        }
        hull.push(points[i]);
    }
    let m = hull.length;
    /* 求出凸包的上半部分 */
    for (let i = n - 2; i >= 0; i--) {
        while (hull.length > m && cross(hull[hull.length - 2], hull[hull.length - 1], points[i]) <= 0) {
            hull.pop();
        }
        hull.push(points[i]);
    }
    /* hull[0] 同时参与凸包的上半部分检测，因此需去掉重复的 hull[0] */
    hull.pop();
    m = hull.length;
    const hullArr = new Array(m).fill(0);
    for (let i = 0; i < m; i++) {
        hullArr[i] = hull[i];
    }
    return hullArr;
}

const triangleArea = (x1, y1, x2, y2, x3, y3) => {
    return 0.5 * Math.abs(x1 * y2 + x2 * y3 + x3 * y1 - x1 * y3 - x2 * y1 - x3 * y2);
}

const cross = (p, q, r) => {
    return (q[0] - p[0]) * (r[1] - q[1]) - (q[1] - p[1]) * (r[0] - q[0]);
};

复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是数组 points 的长度。Andrew 算法的时间复杂度为 O(n \log n)，在凸包上枚举三角形的时间复杂度为 O(n^2)。

  • 空间复杂度：O(n)。Andrew 算法的空间复杂度为 O(n)，保存凸包需要 O(n) 的空间。

 Comments
On this page
0812-最大三角形面积