给定一个无向、连通的树。树中有 n 个标记为 0...n-1 的节点以及 n-1 条边 。
给定整数 n 和数组 edges , edges[i] = [ai, bi]表示树中的节点 ai 和 bi 之间有一条边。
返回长度为 n 的数组 answer ,其中 answer[i] 是树中第 i 个节点与所有其他节点之间的距离之和。
示例 1:
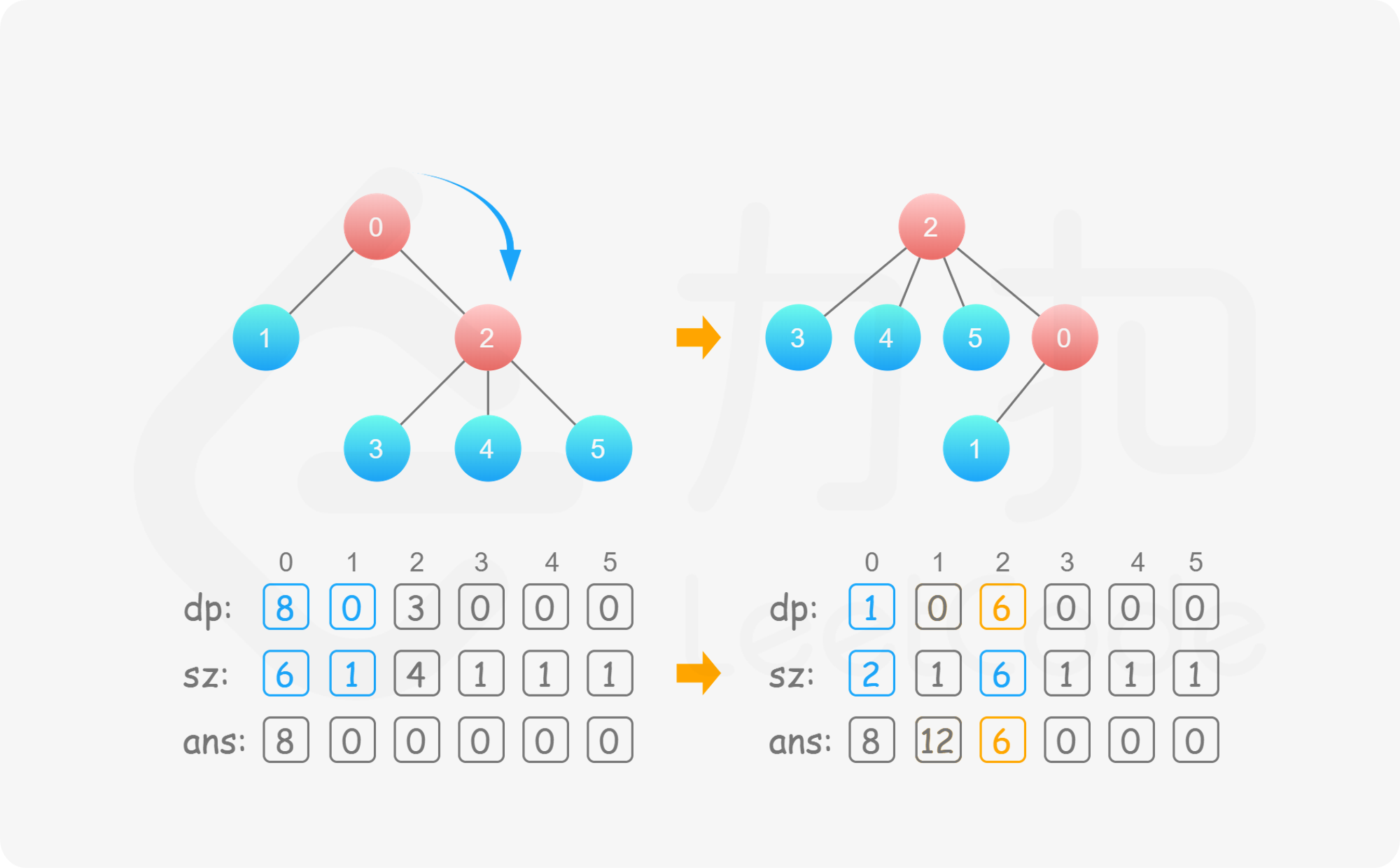
**输入:** n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
**输出:** [8,12,6,10,10,10]
**解释:** 树如图所示。
我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此,answer[0] = 8,以此类推。
示例 2:
**输入:** n = 1, edges = []
**输出:** [0]
示例 3:
**输入:** n = 2, edges = [[1,0]]
**输出:** [1,1]
提示:
1 <= n <= 3 * 104edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != bi给定的输入保证为有效的树
方法一:树形动态规划 思路与算法
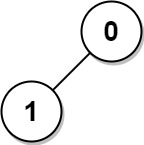
首先我们来考虑一个节点的情况,即每次题目指定一棵树,以 root 为根,询问节点 root 与其他所有节点的距离之和。
很容易想到一个树形动态规划:定义 dp}[u] 表示以 u 为根的子树,它的所有子节点到它的距离之和,同时定义 sz}[u] 表示以 u 为根的子树的节点数量,不难得出如下的转移方程:
\textit{dp}[u]=\sum_{v\in \textit{son}[u]}\textit{dp}[v] + \textit{sz}[v]
其中 son}[u] 表示 u 的所有后代节点集合。转移方程表示的含义就是考虑每个后代节点 v,已知 v 的所有子节点到它的距离之和为 dp}[v],那么这些节点到 u 的距离之和还要考虑 u\rightarrow v 这条边的贡献。考虑这条边长度为 1,一共有 sz[v] 个节点到节点 u 的距离会包含这条边,因此贡献即为 1\times \textit{sz}[v]=\textit{sz}[v]。我们遍历整棵树,从叶子节点开始自底向上递推到根节点 root 即能得出最后的答案为 dp}[\textit{root}]。
回到本题中,题目要求的其实是上题的扩展,即要求我们求出每个节点为根节点的时候,它与其他所有节点的距离之和。暴力的角度我们可以考虑对每个节点都做一次如上的树形动态规划,这样时间复杂度即为 O(n^2),那么有没有更优雅的方法呢?
经过一次树形动态规划后其实我们获得了在 u 为根的树中,每个节点为根的子树的答案 dp,我们可以利用这些已有信息来优化时间复杂度。
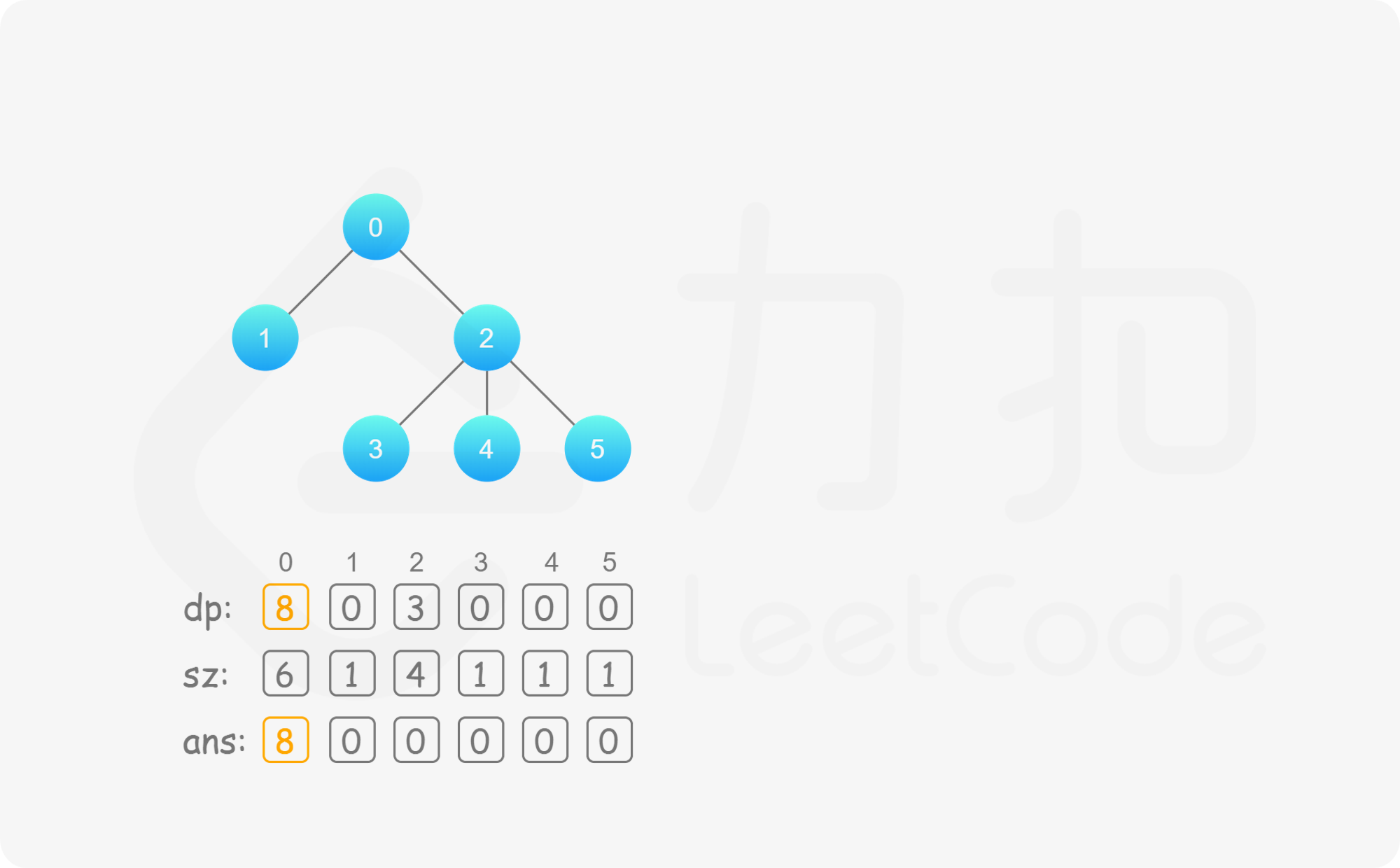
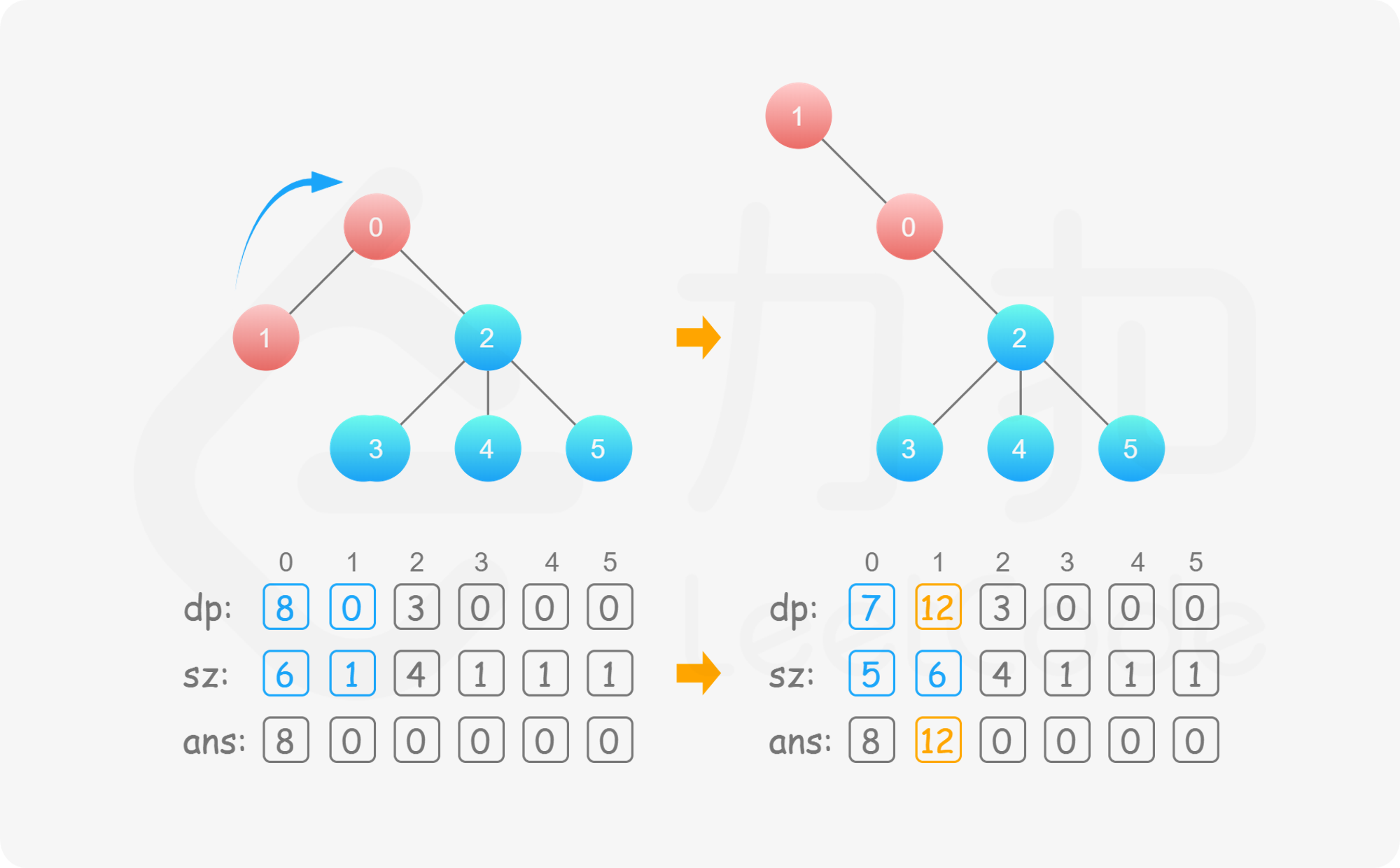
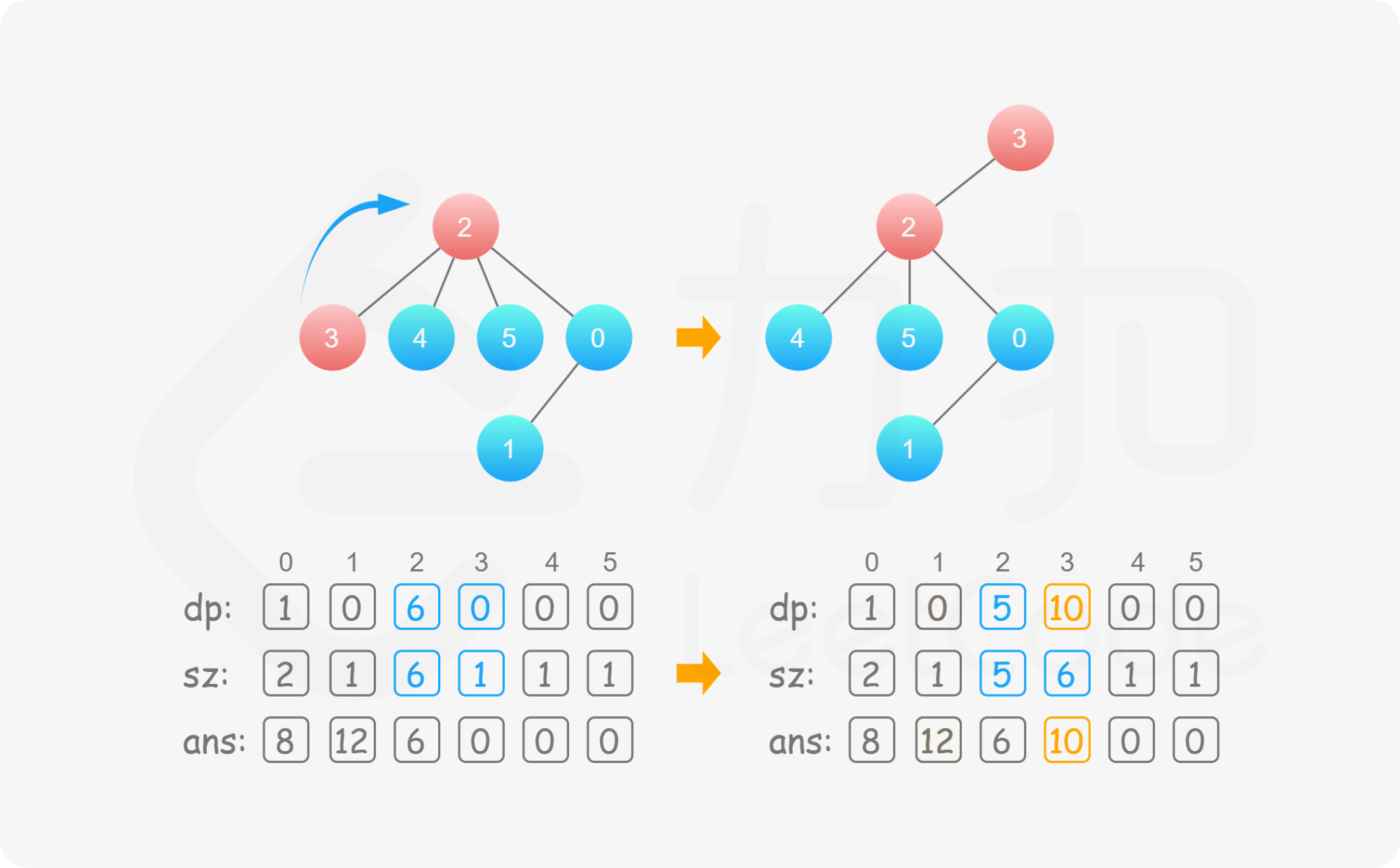
假设 u 的某个后代节点为 v,如果要算 v 的答案,本来我们要以 v 为根来进行一次树形动态规划。但是利用已有的信息,我们可以考虑树的形态做一次改变,让 v 换到根的位置,u 变为其孩子节点,同时维护原有的 dp 信息 。在这一次的转变中,我们观察到除了 u 和 v 的 dp 值,其他节点的 dp 值都不会改变,因此只要更新 dp}[u] 和 dp}[v] 的值即可。
那么我们来看 v 换到根的位置的时候怎么利用已有信息求出 dp}[u] 和 dp}[v] 的值。重新回顾第一次树形动态规划的转移方程,我们可以知道当 u 变为 v 的孩子的时候 v 不在 u 的后代集合 son}[u] 中了,因此此时 dp}[u] 需要减去 v 的贡献,即
\textit{dp}[u]=\textit{dp}[u]-(\textit{dp}[v]+\textit{sz}[v])
同时 sz}[u] 也要相应减去 sz}[v]。
而 v 的后代节点集合中多出了 u,因此 dp}[v] 的值要由 u 更新上来,即
\textit{dp}[v]=\textit{dp}[v]+(\textit{dp}[u]+\textit{sz}[u])
同时 sz}[v] 也要相应加上 sz}[u]。
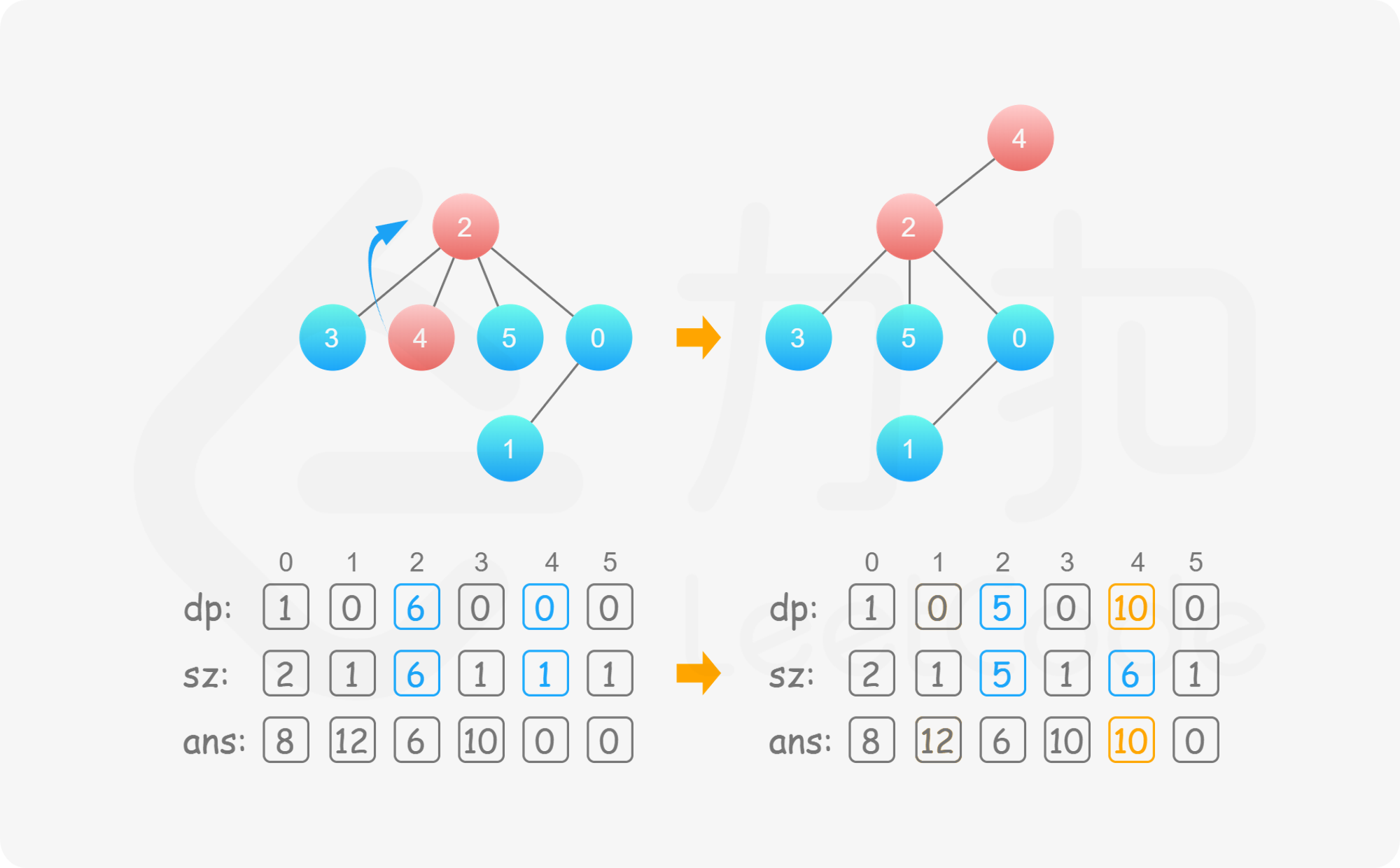
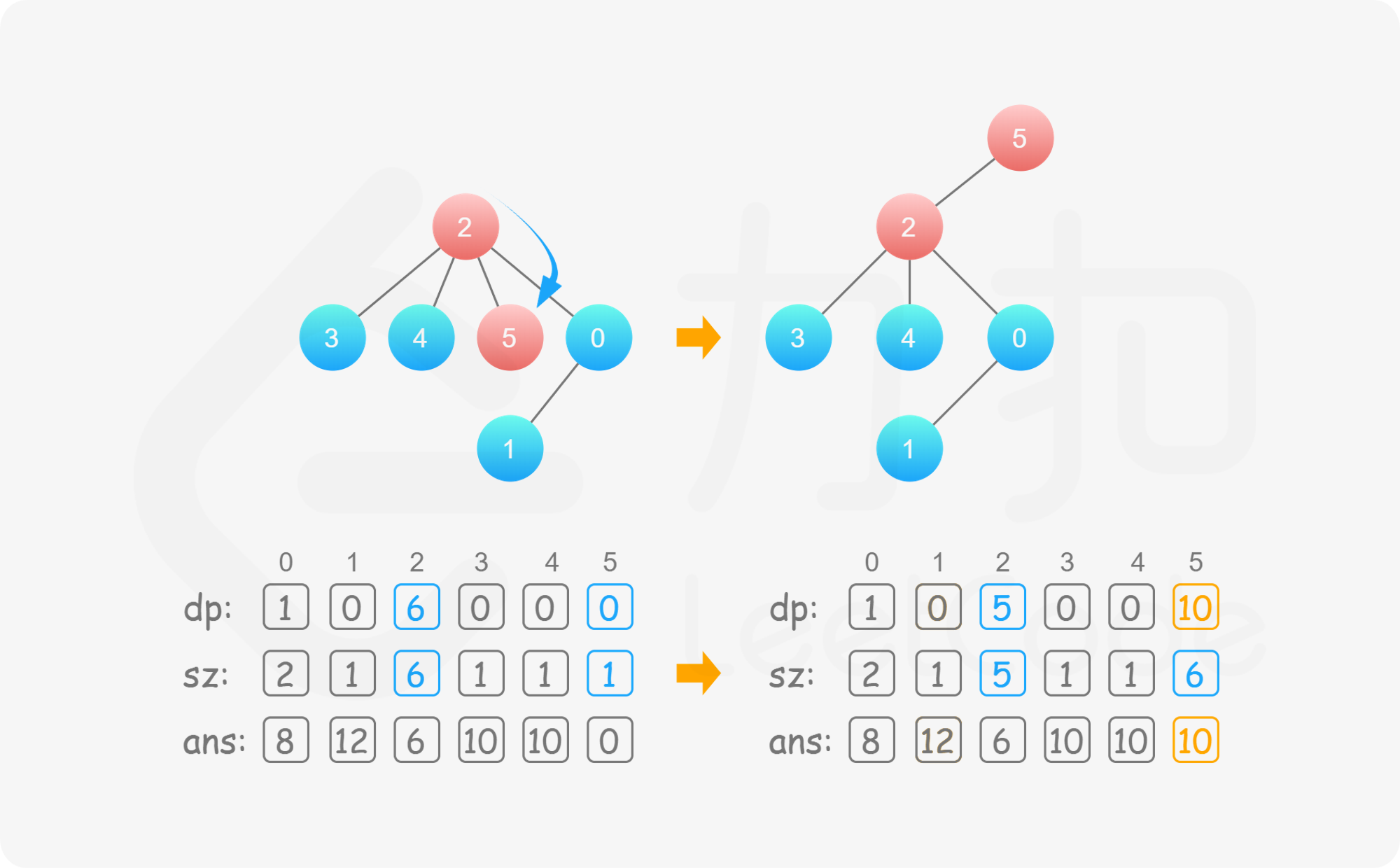
至此我们完成了一次「换根」操作,在 O(1) 的时间内维护了 dp 的信息,且此时的树结构以 v 为根。那么接下来我们不断地进行换根的操作,即能在 O(n) 的时间内求出每个节点为根的答案,实现了时间复杂度的优化。
<
代码
[sol1-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 class Solution {public : vector<int > ans, sz, dp; vector<vector<int >> graph; void dfs (int u, int f) sz[u] = 1 ; dp[u] = 0 ; for (auto & v: graph[u]) { if (v == f) { continue ; } dfs (v, u); dp[u] += dp[v] + sz[v]; sz[u] += sz[v]; } } void dfs2 (int u, int f) ans[u] = dp[u]; for (auto & v: graph[u]) { if (v == f) { continue ; } int pu = dp[u], pv = dp[v]; int su = sz[u], sv = sz[v]; dp[u] -= dp[v] + sz[v]; sz[u] -= sz[v]; dp[v] += dp[u] + sz[u]; sz[v] += sz[u]; dfs2 (v, u); dp[u] = pu, dp[v] = pv; sz[u] = su, sz[v] = sv; } } vector<int > sumOfDistancesInTree (int n, vector<vector<int >>& edges) { ans.resize (n, 0 ); sz.resize (n, 0 ); dp.resize (n, 0 ); graph.resize (n, {}); for (auto & edge: edges) { int u = edge[0 ], v = edge[1 ]; graph[u].emplace_back (v); graph[v].emplace_back (u); } dfs (0 , -1 ); dfs2 (0 , -1 ); return ans; } };
[sol1-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 class Solution { int [] ans; int [] sz; int [] dp; List<List<Integer>> graph; public int [] sumOfDistancesInTree(int n, int [][] edges) { ans = new int [n]; sz = new int [n]; dp = new int [n]; graph = new ArrayList <List<Integer>>(); for (int i = 0 ; i < n; ++i) { graph.add(new ArrayList <Integer>()); } for (int [] edge: edges) { int u = edge[0 ], v = edge[1 ]; graph.get(u).add(v); graph.get(v).add(u); } dfs(0 , -1 ); dfs2(0 , -1 ); return ans; } public void dfs (int u, int f) { sz[u] = 1 ; dp[u] = 0 ; for (int v: graph.get(u)) { if (v == f) { continue ; } dfs(v, u); dp[u] += dp[v] + sz[v]; sz[u] += sz[v]; } } public void dfs2 (int u, int f) { ans[u] = dp[u]; for (int v: graph.get(u)) { if (v == f) { continue ; } int pu = dp[u], pv = dp[v]; int su = sz[u], sv = sz[v]; dp[u] -= dp[v] + sz[v]; sz[u] -= sz[v]; dp[v] += dp[u] + sz[u]; sz[v] += sz[u]; dfs2(v, u); dp[u] = pu; dp[v] = pv; sz[u] = su; sz[v] = sv; } } }
[sol1-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 let ans, sz, dp, graph;const dfs = (u, f ) => { sz[u] = 1 ; dp[u] = 0 ; for (const v of graph[u]) { if (v === f) { continue ; } dfs (v, u); dp[u] += dp[v] + sz[v]; sz[u] += sz[v]; } } const dfs2 = (u, f ) => { ans[u] = dp[u]; for (const v of graph[u]) { if (v === f) { continue ; } const pu = dp[u], pv = dp[v]; const su = sz[u], sv = sz[v]; dp[u] -= dp[v] + sz[v]; sz[u] -= sz[v]; dp[v] += dp[u] + sz[u]; sz[v] += sz[u]; dfs2 (v, u); dp[u] = pu, dp[v] = pv; sz[u] = su, sz[v] = sv; } } var sumOfDistancesInTree = function (n, edges ) { ans = new Array (n).fill (0 ); sz = new Array (n).fill (0 ); dp = new Array (n).fill (0 ); graph = new Array (n).fill (0 ).map (v => for (const [u, v] of edges) { graph[u].push (v); graph[v].push (u); } dfs (0 , -1 ); dfs2 (0 , -1 ); return ans; };
[sol1-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 func sumOfDistancesInTree (n int , edges [][]int ) int { graph := make ([][]int , n) for _, e := range edges { u, v := e[0 ], e[1 ] graph[u] = append (graph[u], v) graph[v] = append (graph[v], u) } sz := make ([]int , n) dp := make ([]int , n) var dfs func (u, f int ) dfs = func (u, f int ) sz[u] = 1 for _, v := range graph[u] { if v == f { continue } dfs(v, u) dp[u] += dp[v] + sz[v] sz[u] += sz[v] } } dfs(0 , -1 ) ans := make ([]int , n) var dfs2 func (u, f int ) dfs2 = func (u, f int ) ans[u] = dp[u] for _, v := range graph[u] { if v == f { continue } pu, pv := dp[u], dp[v] su, sv := sz[u], sz[v] dp[u] -= dp[v] + sz[v] sz[u] -= sz[v] dp[v] += dp[u] + sz[u] sz[v] += sz[u] dfs2(v, u) dp[u], dp[v] = pu, pv sz[u], sz[v] = su, sv } } dfs2(0 , -1 ) return ans }
[sol1-C] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 int *ans, *sz, *dp;int *hd, *nx, *e;void dfs (int u, int f) { sz[u] = 1 ; dp[u] = 0 ; for (int i = hd[u]; i; i = nx[i]) { int v = e[i]; if (v == f) { continue ; } dfs(v, u); dp[u] += dp[v] + sz[v]; sz[u] += sz[v]; } } void dfs2 (int u, int f) { ans[u] = dp[u]; for (int i = hd[u]; i; i = nx[i]) { int v = e[i]; if (v == f) { continue ; } int pu = dp[u], pv = dp[v]; int su = sz[u], sv = sz[v]; dp[u] -= dp[v] + sz[v]; sz[u] -= sz[v]; dp[v] += dp[u] + sz[u]; sz[v] += sz[u]; dfs2(v, u); dp[u] = pu, dp[v] = pv; sz[u] = su, sz[v] = sv; } } int * sumOfDistancesInTree (int n, int ** edges, int edgesSize, int * edgesColSize, int * returnSize) { ans = malloc (sizeof (int ) * n); sz = malloc (sizeof (int ) * n); dp = malloc (sizeof (int ) * n); hd = malloc (sizeof (int ) * n); nx = malloc (sizeof (int ) * (edgesSize * 2 + 1 )); e = malloc (sizeof (int ) * (edgesSize * 2 + 1 )); for (int i = 0 ; i < n; i++) { ans[i] = sz[i] = dp[i] = hd[i] = 0 ; } for (int i = 0 , num = 0 ; i < edgesSize; i++) { int u = edges[i][0 ], v = edges[i][1 ]; nx[++num] = hd[u], hd[u] = num, e[num] = v; nx[++num] = hd[v], hd[v] = num, e[num] = u; } dfs(0 , -1 ); dfs2(0 , -1 ); *returnSize = n; return ans; }
复杂度分析


 ,
, ,
, ,
, ,
, ,
, ,
, >
>