0840-矩阵中的幻方

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:28 2023-09-13 16:06:28 Updated    

3 x 3 的幻方是一个填充有 **从1 到 9 ** 的不同数字的 3 x 3 矩阵，其中每行，每列以及两条对角线上的各数之和都相等。

给定一个由整数组成的row x col 的 grid，其中有多少个 3 × 3 的 “幻方” 子矩阵？（每个子矩阵都是连续的）。

示例 1：

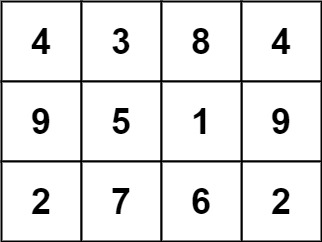
**输入:** grid = [[4,3,8,4],[9,5,1,9],[2,7,6,2]
**输出:** 1
**解释:**
下面的子矩阵是一个 3 x 3 的幻方：
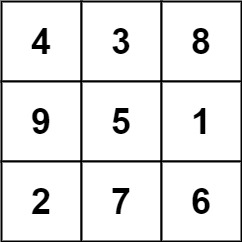
![](https://assets.leetcode.com/uploads/2020/09/11/magic_valid.jpg)
而这一个不是：
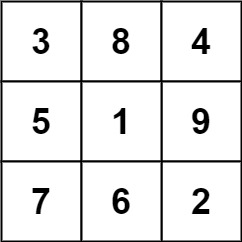
![](https://assets.leetcode.com/uploads/2020/09/11/magic_invalid.jpg)
总的来说，在本示例所给定的矩阵中只有一个 3 x 3 的幻方子矩阵。

示例 2:

**输出:** grid = [[8]]
**输入:** 0

提示:

  • row == grid.length
  • col == grid[i].length
  • 1 <= row, col <= 10
  • 0 <= grid[i][j] <= 15

方法一：暴力法

算法：

我们分别检查每 3x3 的网格。对于每个网格，所有数字必须不同，并且在 1 到 9 之间；且每一个行，列，对角线的和必须相同。

额外的加分项：

我们可以在代码中添加 if grid[r+1][c+1] != 5: continue，帮助我们略过一些循环，这是基于以下观察得出：

  • 网格的总和是 45，因为网格必须是 1 到 9 不同的数字。
  • 每一列和行加起来必须是 15，乘以 3 则是网格的总和。
  • 对角线的和也必须是 15，题目中说了对角线与列，行的和相同。
  • 将四条穿过中心的线的 12 个值相加（即一行一列两条对角线），这四条线加起来等于 60；而整个网格加起来为 45。则中心等于 （60-45）/3 = 5。
[solution1-Python]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution(object):
    def numMagicSquaresInside(self, grid):
        R, C = len(grid), len(grid[0])

        def magic(a,b,c,d,e,f,g,h,i):
            return (sorted([a,b,c,d,e,f,g,h,i]) == range(1, 10) and
                (a+b+c == d+e+f == g+h+i == a+d+g ==
                 b+e+h == c+f+i == a+e+i == c+e+g == 15))

        ans = 0
        for r in xrange(R-2):
            for c in xrange(C-2):
                if grid[r+1][c+1] != 5: continue  # optional skip
                if magic(grid[r][c], grid[r][c+1], grid[r][c+2],
                         grid[r+1][c], grid[r+1][c+1], grid[r+1][c+2],
                         grid[r+2][c], grid[r+2][c+1], grid[r+2][c+2]):
                    ans += 1
        return ans
[solution1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
    public int numMagicSquaresInside(int[][] grid) {
        int R = grid.length, C = grid[0].length;
        int ans = 0;
        for (int r = 0; r < R-2; ++r)
            for (int c = 0; c < C-2; ++c) {
                if (grid[r+1][c+1] != 5) continue;  // optional skip
                if (magic(grid[r][c], grid[r][c+1], grid[r][c+2],
                          grid[r+1][c], grid[r+1][c+1], grid[r+1][c+2],
                          grid[r+2][c], grid[r+2][c+1], grid[r+2][c+2]))
                    ans++;
            }

        return ans;
    }

    public boolean magic(int... vals) {
        int[] count = new int[16];
        for (int v: vals) count[v]++;
        for (int v = 1; v <= 9; ++v)
            if (count[v] != 1)
                return false;

        return (vals[0] + vals[1] + vals[2] == 15 &&
                vals[3] + vals[4] + vals[5] == 15 &&
                vals[6] + vals[7] + vals[8] == 15 &&
                vals[0] + vals[3] + vals[6] == 15 &&
                vals[1] + vals[4] + vals[7] == 15 &&
                vals[2] + vals[5] + vals[8] == 15 &&
                vals[0] + vals[4] + vals[8] == 15 &&
                vals[2] + vals[4] + vals[6] == 15);
    }
}

复杂度分析

  • 时间复杂度：O(R*C)。其中 R, C 指的是给定 grid 的行和列。
  • 空间复杂度：O(1)。
 Comments
On this page
0840-矩阵中的幻方