给你一个大小为 m x n 的二元矩阵 grid ,矩阵中每个元素的值为 0 或 1 。
一次 移动 是指选择任一行或列,并转换该行或列中的每一个值:将所有 0 都更改为 1,将所有 1 都更改为 0。
在做出任意次数的移动后,将该矩阵的每一行都按照二进制数来解释,矩阵的 得分 就是这些数字的总和。
在执行任意次 移动 后(含 0 次),返回可能的最高分数。
示例 1:

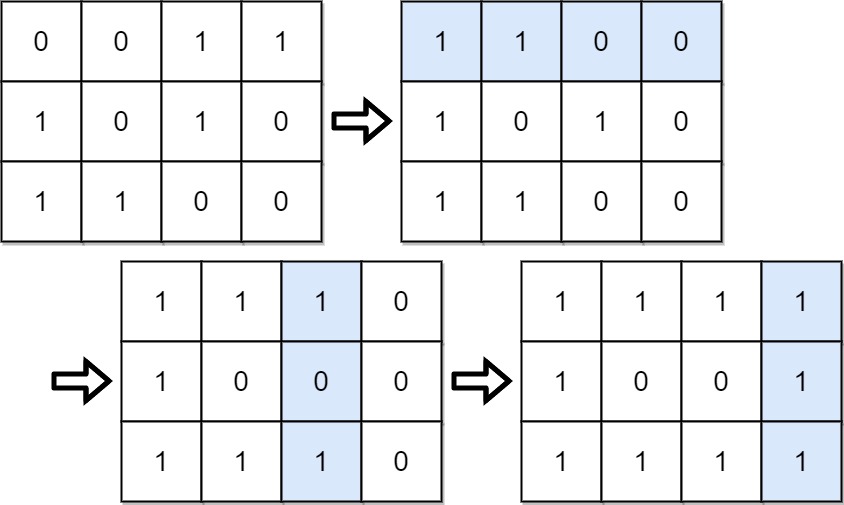
**输入:** grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
**输出:** 39
**解释:** 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39
示例 2:
**输入:** grid = [[0]]
**输出:** 1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 20grid[i][j] 为 0 或 1
方法一:贪心
根据题意,能够知道一个重要的事实:给定一个翻转方案,则它们之间任意交换顺序后,得到的结果保持不变。因此,我们总可以先考虑所有的行翻转,再考虑所有的列翻转。
不难发现一点:为了得到最高的分数,矩阵的每一行的最左边的数都必须为 1。为了做到这一点,我们可以翻转那些最左边的数不为 1 的那些行,而其他的行则保持不动。
当将每一行的最左边的数都变为 1 之后,就只能进行列翻转了。为了使得总得分最大,我们要让每个列中 1 的数目尽可能多。因此,我们扫描除了最左边的列以外的每一列,如果该列 0 的数目多于 1 的数目,就翻转该列,其他的列则保持不变。
实际编写代码时,我们无需修改原矩阵,而是可以计算每一列对总分数的「贡献」,从而直接计算出最高的分数。假设矩阵共有 m 行 n 列,计算方法如下:
对于最左边的列而言,由于最优情况下,它们的取值都为 1,因此每个元素对分数的贡献都为 2^{n-1,总贡献为 m \times 2^{n-1。
对于第 j 列(j>0,此处规定最左边的列是第 0 列)而言,我们统计这一列 0,1 的数量,令其中的最大值为 k,则 k 是列翻转后的 1 的数量,该列的总贡献为 k \times 2^{n-j-1。需要注意的是,在统计 0,1 的数量的时候,要考虑最初进行的行反转。
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
int matrixScore(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int ret = m * (1 << (n - 1));
for (int j = 1; j < n; j++) {
int nOnes = 0;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]);
}
}
int k = max(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int matrixScore(int[][] grid) {
int m = grid.length, n = grid[0].length;
int ret = m * (1 << (n - 1));
for (int j = 1; j < n; j++) {
int nOnes = 0;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]);
}
}
int k = Math.max(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
}
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| func matrixScore(grid [][]int) int {
m, n := len(grid), len(grid[0])
ans := 1 << (n - 1) * m
for j := 1; j < n; j++ {
ones := 0
for _, row := range grid {
if row[j] == row[0] {
ones++
}
}
if ones < m-ones {
ones = m - ones
}
ans += 1 << (n - 1 - j) * ones
}
return ans
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| var matrixScore = function(grid) {
const m = grid.length, n = grid[0].length;
let ret = m * (1 << (n - 1));
for (let j = 1; j < n; j++) {
let nOnes = 0;
for (let i = 0; i < m; i++) {
if (grid[i][0] === 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]);
}
}
const k = Math.max(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
};
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| int matrixScore(int** grid, int gridSize, int* gridColSize) {
int m = gridSize, n = gridColSize[0];
int ret = m * (1 << (n - 1));
for (int j = 1; j < n; j++) {
int nOnes = 0;
for (int i = 0; i < m; i++) {
if (grid[i][0] == 1) {
nOnes += grid[i][j];
} else {
nOnes += (1 - grid[i][j]);
}
}
int k = fmax(nOnes, m - nOnes);
ret += k * (1 << (n - j - 1));
}
return ret;
}
|
复杂度分析