0863-二叉树中所有距离为 K 的结点

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:31 2023-09-13 16:06:31 Updated    

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 k 。

返回到目标结点 target 距离为 k 的所有结点的值的列表。 答案可以以 任何顺序 返回。

示例 1：

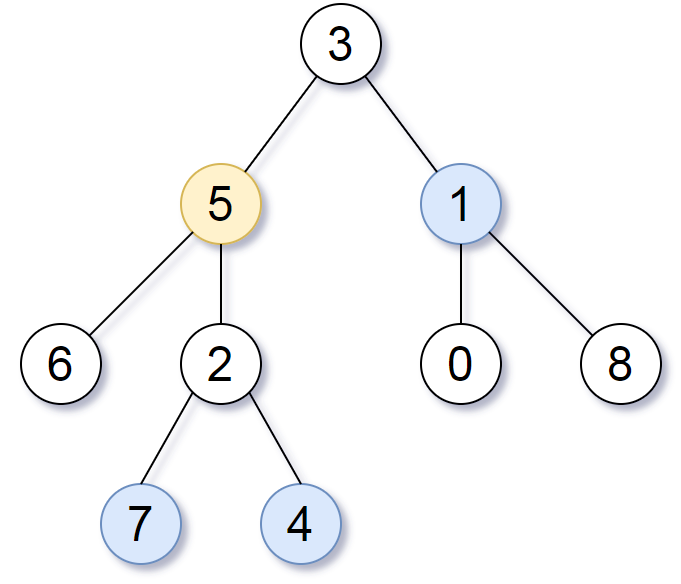
**输入：** root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
**输出：** [7,4,1]
**解释：** 所求结点为与目标结点（值为 5）距离为 2 的结点，值分别为 7，4，以及 1

示例 2:

**输入:** root = [1], target = 1, k = 3
**输出:** []

提示:

  • 节点数在 [1, 500] 范围内
  • 0 <= Node.val <= 500
  • Node.val 中所有值 不同
  • 目标结点 target 是树上的结点。
  • 0 <= k <= 1000

方法一：深度优先搜索 + 哈希表

若将 target 当作树的根结点，我们就能从 target 出发，使用深度优先搜索去寻找与 target 距离为 k 的所有结点，即深度为 k 的所有结点。

由于输入的二叉树没有记录父结点，为此，我们从根结点 root 出发，使用深度优先搜索遍历整棵树，同时用一个哈希表记录每个结点的父结点。

然后从 target 出发，使用深度优先搜索遍历整棵树，除了搜索左右儿子外，还可以顺着父结点向上搜索。

代码实现时，由于每个结点值都是唯一的，哈希表的键可以用结点值代替。此外，为避免在深度优先搜索时重复访问结点，递归时额外传入来源结点 from，在递归前比较目标结点是否与来源结点相同，不同的情况下才进行递归。

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Solution {
    unordered_map<int, TreeNode*> parents;
    vector<int> ans;

    void findParents(TreeNode* node) {
        if (node->left != nullptr) {
            parents[node->left->val] = node;
            findParents(node->left);
        }
        if (node->right != nullptr) {
            parents[node->right->val] = node;
            findParents(node->right);
        }
    }

    void findAns(TreeNode* node, TreeNode* from, int depth, int k) {
        if (node == nullptr) {
            return;
        }
        if (depth == k) {
            ans.push_back(node->val);
            return;
        }
        if (node->left != from) {
            findAns(node->left, node, depth + 1, k);
        }
        if (node->right != from) {
            findAns(node->right, node, depth + 1, k);
        }
        if (parents[node->val] != from) {
            findAns(parents[node->val], node, depth + 1, k);
        }
    }

public:
    vector<int> distanceK(TreeNode* root, TreeNode* target, int k) {
        // 从 root 出发 DFS，记录每个结点的父结点
        findParents(root);

        // 从 target 出发 DFS，寻找所有深度为 k 的结点
        findAns(target, nullptr, 0, k);

        return ans;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    Map<Integer, TreeNode> parents = new HashMap<Integer, TreeNode>();
    List<Integer> ans = new ArrayList<Integer>();

    public List<Integer> distanceK(TreeNode root, TreeNode target, int k) {
        // 从 root 出发 DFS，记录每个结点的父结点
        findParents(root);

        // 从 target 出发 DFS，寻找所有深度为 k 的结点
        findAns(target, null, 0, k);

        return ans;
    }

    public void findParents(TreeNode node) {
        if (node.left != null) {
            parents.put(node.left.val, node);
            findParents(node.left);
        }
        if (node.right != null) {
            parents.put(node.right.val, node);
            findParents(node.right);
        }
    }

    public void findAns(TreeNode node, TreeNode from, int depth, int k) {
        if (node == null) {
            return;
        }
        if (depth == k) {
            ans.add(node.val);
            return;
        }
        if (node.left != from) {
            findAns(node.left, node, depth + 1, k);
        }
        if (node.right != from) {
            findAns(node.right, node, depth + 1, k);
        }
        if (parents.get(node.val) != from) {
            findAns(parents.get(node.val), node, depth + 1, k);
        }
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class Solution {
    Dictionary<int, TreeNode> parents = new Dictionary<int, TreeNode>();
    IList<int> ans = new List<int>();

    public IList<int> DistanceK(TreeNode root, TreeNode target, int k) {
        // 从 root 出发 DFS，记录每个结点的父结点
        FindParents(root);

        // 从 target 出发 DFS，寻找所有深度为 k 的结点
        FindAns(target, null, 0, k);

        return ans;
    }

    public void FindParents(TreeNode node) {
        if (node.left != null) {
            parents.Add(node.left.val, node);
            FindParents(node.left);
        }
        if (node.right != null) {
            parents.Add(node.right.val, node);
            FindParents(node.right);
        }
    }

    public void FindAns(TreeNode node, TreeNode from, int depth, int k) {
        if (node == null) {
            return;
        }
        if (depth == k) {
            ans.Add(node.val);
            return;
        }
        if (node.left != from) {
            FindAns(node.left, node, depth + 1, k);
        }
        if (node.right != from) {
            FindAns(node.right, node, depth + 1, k);
        }
        TreeNode parent = parents.ContainsKey(node.val) ? parents[node.val] : null;
        if (parent != from) {
            FindAns(parent, node, depth + 1, k);
        }
    }
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
func distanceK(root, target *TreeNode, k int) (ans []int) {
    // 从 root 出发 DFS，记录每个结点的父结点
    parents := map[int]*TreeNode{}
    var findParents func(*TreeNode)
    findParents = func(node *TreeNode) {
        if node.Left != nil {
            parents[node.Left.Val] = node
            findParents(node.Left)
        }
        if node.Right != nil {
            parents[node.Right.Val] = node
            findParents(node.Right)
        }
    }
    findParents(root)

    // 从 target 出发 DFS，寻找所有深度为 k 的结点
    var findAns func(*TreeNode, *TreeNode, int)
    findAns = func(node, from *TreeNode, depth int) {
        if node == nil {
            return
        }
        if depth == k { // 将所有深度为 k 的结点的值计入结果
            ans = append(ans, node.Val)
            return
        }
        if node.Left != from {
            findAns(node.Left, node, depth+1)
        }
        if node.Right != from {
            findAns(node.Right, node, depth+1)
        }
        if parents[node.Val] != from {
            findAns(parents[node.Val], node, depth+1)
        }
    }
    findAns(target, nil, 0)
    return
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
struct HashTable {
    int key;
    struct TreeNode* val;
    UT_hash_handle hh;
};

void modify(struct HashTable** hashTable, int ikey, struct HashTable* ival) {
    struct HashTable* iter;
    HASH_FIND_INT(*hashTable, &ikey, iter);
    if (iter == NULL) {
        iter = malloc(sizeof(struct HashTable));
        iter->key = ikey;
        iter->val = ival;
        HASH_ADD_INT(*hashTable, key, iter);
    } else {
        iter->val = ival;
    }
}

struct HashTable* query(struct HashTable** hashTable, int ikey) {
    struct HashTable* iter;
    HASH_FIND_INT(*hashTable, &ikey, iter);
    if (iter == NULL) {
        return NULL;
    }
    return iter->val;
}

struct HashTable* parents;
int* ans;
int ansSize;

void findParents(struct TreeNode* node) {
    if (node->left != NULL) {
        modify(&parents, node->left->val, node);
        findParents(node->left);
    }
    if (node->right != NULL) {
        modify(&parents, node->right->val, node);
        findParents(node->right);
    }
}

void findAns(struct TreeNode* node, struct TreeNode* from, int depth, int k) {
    if (node == NULL) {
        return;
    }
    if (depth == k) {
        ans[ansSize++] = node->val;
        return;
    }
    if (node->left != from) {
        findAns(node->left, node, depth + 1, k);
    }
    if (node->right != from) {
        findAns(node->right, node, depth + 1, k);
    }
    if (query(&parents, node->val) != from) {
        findAns(query(&parents, node->val), node, depth + 1, k);
    }
}

int* distanceK(struct TreeNode* root, struct TreeNode* target, int k, int* returnSize) {
    parents = NULL;
    ans = malloc(sizeof(int) * 500);
    ansSize = 0;

    // 从 root 出发 DFS，记录每个结点的父结点
    findParents(root);

    // 从 target 出发 DFS，寻找所有深度为 k 的结点
    findAns(target, NULL, 0, k);

    *returnSize = ansSize;
    return ans;
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
var distanceK = function(root, target, k) {
    const parents = new Map();
    const ans = [];

    const findParents = (node) => {
        if (node.left != null) {
            parents.set(node.left.val, node);
            findParents(node.left);
        }
        if (node.right != null) {
            parents.set(node.right.val, node);
            findParents(node.right);
        }
    }

    // 从 root 出发 DFS，记录每个结点的父结点
    findParents(root);

    const findAns = (node, from, depth, k) => {
        if (node == null) {
            return;
        }
        if (depth === k) {
            ans.push(node.val);
            return;
        }
        if (node.left !== from) {
            findAns(node.left, node, depth + 1, k);
        }
        if (node.right !== from) {
            findAns(node.right, node, depth + 1, k);
        }
        if (parents.get(node.val) !== from) {
            findAns(parents.get(node.val), node, depth + 1, k);
        }
    }
    // 从 target 出发 DFS，寻找所有深度为 k 的结点
    findAns(target, null, 0, k);

    return ans;
};

复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的结点个数。需要执行两次深度优先搜索，每次的时间复杂度均为 O(n)。

  • 空间复杂度：O(n)。记录父节点需要 O(n) 的空间，深度优先搜索需要 O(n) 的栈空间。

 Comments
On this page
0863-二叉树中所有距离为 K 的结点