0876-链表的中间结点

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:23 2023-09-13 16:06:23 Updated    

给你单链表的头结点 head ，请你找出并返回链表的中间结点。

如果有两个中间结点，则返回第二个中间结点。

示例 1：

**输入：** head = [1,2,3,4,5]
**输出：** [3,4,5]
**解释：** 链表只有一个中间结点，值为 3 。

示例 2：

**输入：** head = [1,2,3,4,5,6]
**输出：** [4,5,6]
**解释：** 该链表有两个中间结点，值分别为 3 和 4 ，返回第二个结点。

提示：

  • 链表的结点数范围是 [1, 100]
  • 1 <= Node.val <= 100

朴素解法：这道题最朴素的做法是，先遍历一次，计算链表的长度，进而计算链表中间结点的下标（注意偶数结点的时候，得到的是中间的第二个结点），然后再遍历一次，来到所要求结点的位置。

缺点：

  • 必须先遍历完整个链表，然后才可以「干正事」，再遍历到一半，找到中间结点；
  • 在链表的长度很长的时候，这种方法之前的等待会很久。

快慢指针：比较经典的做法是：

  • 使用两个指针变量，刚开始都位于链表的第 1 个结点，一个永远一次只走 1 步，一个永远一次只走 2 步，一个在前，一个在后，同时走。这样当快指针走完的时候，慢指针就来到了链表的中间位置。

思想是：快慢指针的前进方向相同，且它们步伐的「差」是恒定的，根据这种确定性去解决链表中的一些问题。使用这种思想还可以解决链表的以下问题：

  • 「力扣」第 19 题： 倒数第 k 个结点 ，快指针先走几步，不是靠猜的，要在纸上画图模拟一下，就清楚了；
  • 「力扣」第 141 题：环形链表 ，在环中的时候可以想象，A 同学开始有存款 100 元，每天赚 1 元，B 同学开始有存款 50 元，每天赚 2 元，B 同学一定会在某一天和 A 同学的存款一样；
  • 「力扣」第 142 题：环形链表 II ；
  • 「力扣」第 161 题：相交链表 ，起点不同，构造相同长度让它们相遇，同样是利用了同步走这个等量关系。

解决这些问题的共同特点就是使用两个指针变量同步移动。解决链表的问题常见的技巧还有：

  • 1、使用递归函数，避免复杂的更改指针变量指向操作，使得求解问题变得简单。
  • 2、设置「虚拟头结点」，避免对链表第 1 个结点做单独讨论，这个思想在数组里我们见过，叫「哨兵」；
  • 3、使用「快慢指针」，本题就是。确切地说，叫「同步指针」可能更好一些；
  • 4、为链表编写测试函数，进行调试（在下面的参考代码中有），主要是：
    • 从数组得到一个链表；
    • 根据当前结点打印当前结点以及后面的结点。
      这两个方法可以非常方便地帮助我们调试关于链表的程序。

大家还可以在「力扣」的新手场：「探索」 板块里，学习链表的相关知识和问题。「力扣」上的链表问题，和我们在教科书里学习的链表是有一点点不一样的，「力扣」的链表是以结点类 ListNode 为中心进行编程。而一般教科书上则是将 ListNode 作为链表的内部类进行编程，差别就是这些。其它处理链表问题的技巧是完全一样的。

打草稿很重要：链表问题在「力扣」上是相对较少，并且题目类型和解题技巧相对固定的问题，相信通过刷题和总结，我们是可以把链表问题全部掌握的。

并且思考链表问题的第 1 步，和「回溯算法」一样，绝大多数时候在草稿纸上写写画画就能得到解决链表问题的办法，特别是在链表中做一些更改指针变量指向操作的问题。

注意：这里要注意一个细节：题目要求：「两个中间结点的时候，返回第二个中间结点」。此时可以在草稿纸上写写画画，就拿自己的左右手的两根指头同步移动，可以得出：快指针可以前进的条件是：当前快指针和当前快指针的下一个结点都非空。

在有些问题，例如「力扣」第 148 题：排序链表 ，是需要来到链表的第一个中间结点，然后切断链表，这时代码就得做小的调整。具体是怎么写的，不能靠猜，依然是要在纸上模拟一下这个「快慢指针同步走」的过程，就很清楚了（不过第 148 题的本来意思不是让我们从中间二分递归去做）。

结论：如果题目要求「在两个中间结点的时候，返回第一个中间结点」，此时快指针可以前进的条件是：当前快指针的下一个结点和当前快指针的下下一个结点都非空。

注意体会以上二者的不同之处。

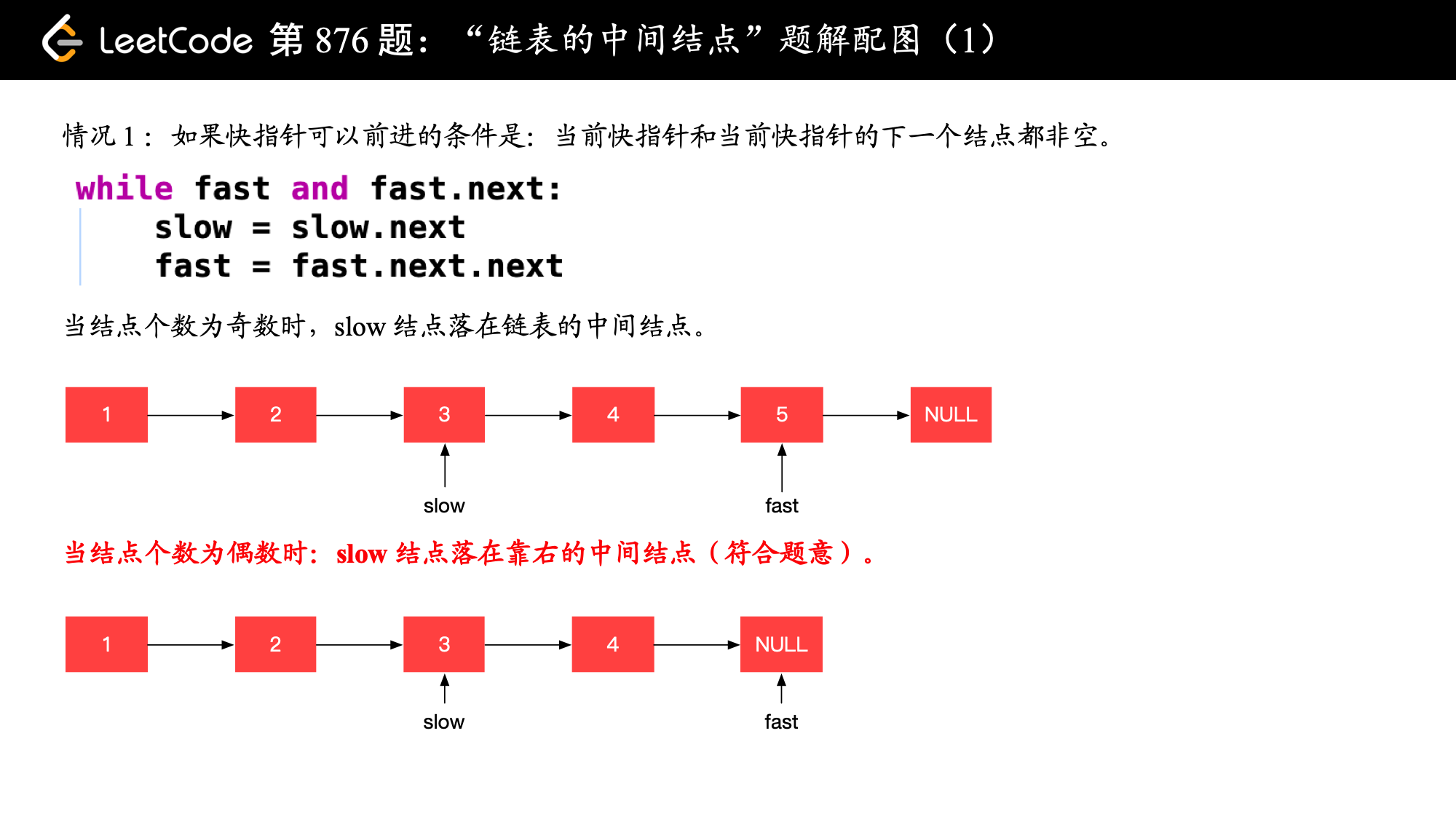
876-1.png
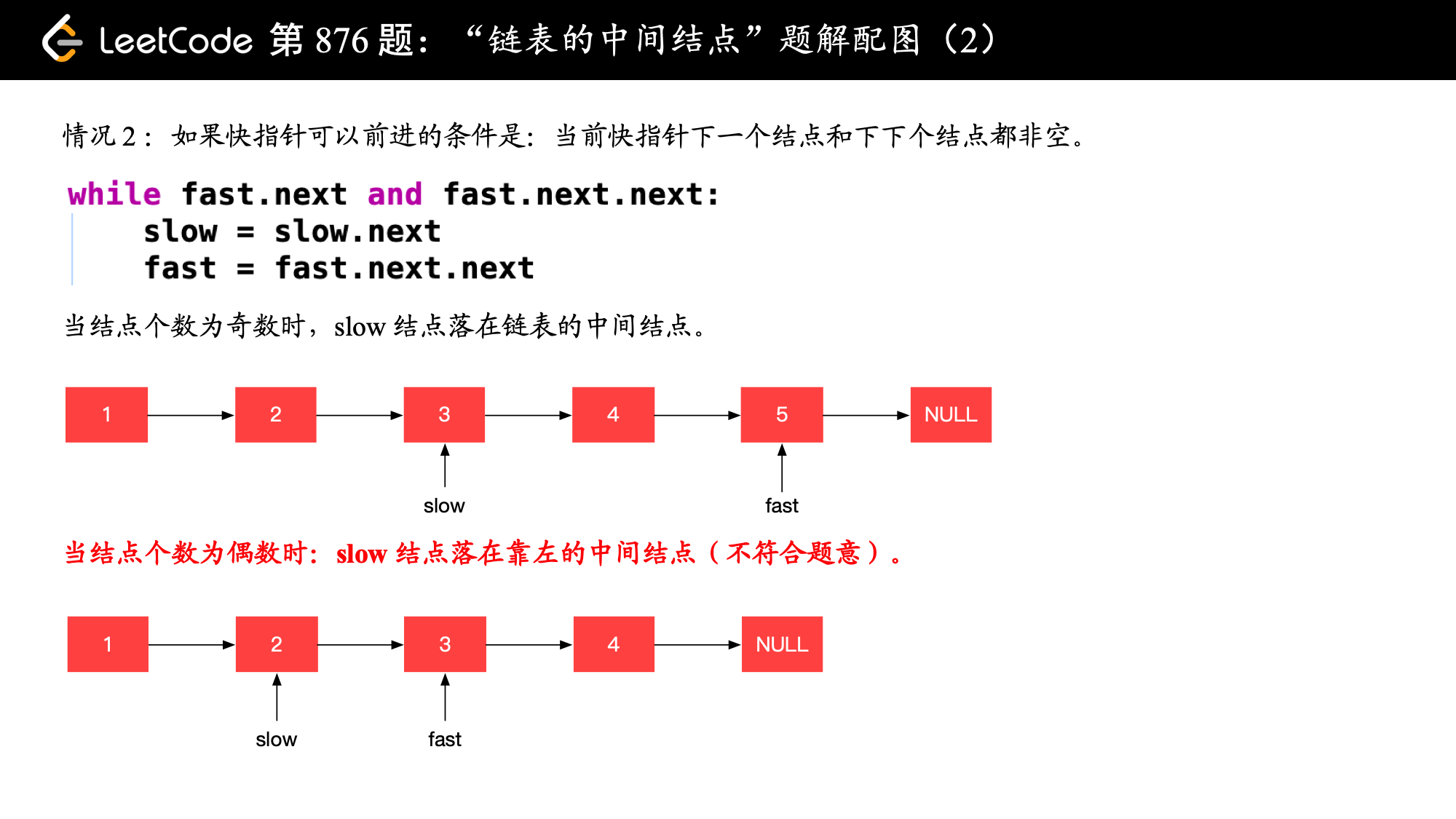
876-2.png

说明：图例中使用了 Python 语言的写法，例如 while fast 在 fast 变量不是空结点的时候，返回 True，写成 while fast is not None 是语义更清晰的写法，但由于约定，且这种写法非常常见，我们就简写了。

参考代码 1：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class ListNode {
    int val;
    ListNode next;

    ListNode(int x) {
        val = x;
    }

    public ListNode(int[] nums) {
        if (nums == null || nums.length == 0) {
            throw new IllegalArgumentException("arr can not be empty");
        }
        this.val = nums[0];
        ListNode curr = this;
        for (int i = 1; i < nums.length; i++) {
            curr.next = new ListNode(nums[i]);
            curr = curr.next;
        }
    }

    @Override
    public String toString() {
        StringBuilder s = new StringBuilder();
        ListNode cur = this;
        while (cur != null) {
            s.append(cur.val);
            s.append(" -> ");
            cur = cur.next;
        }
        s.append("NULL");
        return s.toString();
    }
}

public class Solution {

    public ListNode middleNode(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode slow = head;
        ListNode fast = head;

        while (fast != null && fast.next != null) {
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

    public static void main(String[] args) {
        int[] arr = new int[]{1, 2, 3, 4, 5, 6};
        // int[] arr = new int[]{1, 2, 3, 4, 5};
        ListNode head = new ListNode(arr);
        Solution solution = new Solution();
        ListNode res = solution.middleNode(head);
        System.out.println(res);
    }
}
[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def middleNode(self, head: ListNode) -> ListNode:
        if head is None:
            return None

        slow = head
        fast = head

        while fast and fast.next:
            slow = slow.next
            fast = fast.next.next
        return slow


def create_linked_list(nums):
    if len(nums) == 0:
        return None
    head = ListNode(nums[0])
    cur = head
    for i in range(1, len(nums)):
        cur.next = ListNode(nums[i])
        cur = cur.next
    return head


def print_linked_list(list_node):
    if list_node is None:
        return

    cur = list_node
    while cur:
        print(cur.val, '->', end=' ')
        cur = cur.next
    print('null')


if __name__ == '__main__':
    # nums = [1, 2, 3, 4, 5, 6, 7]
    nums = [1, 2, 3, 4, 5, 6, 7, 8]
    head = create_linked_list(nums)
    solution = Solution()
    result = solution.middleNode(head)
    print('结果：')
    print_linked_list(result)

复杂度分析：

  • 时间复杂度：O(N)，N 是链表的长度，快指针变量需要遍历完整个链表，因此最多走 N 步；
  • 空间复杂度：O(1)。
 Comments
On this page
0876-链表的中间结点