Alice 和 Bob 用几堆石子在做游戏。一共有偶数堆石子, 排成一行 ;每堆都有 正 整数颗石子,数目为 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的 总数 是 奇数 ,所以没有平局。
Alice 和 Bob 轮流进行, Alice 先开始 。 每回合,玩家从行的 开始 或 结束 处取走整堆石头。石子最多 的玩家 获胜 。
假设 Alice 和 Bob 都发挥出最佳水平,当 Alice 赢得比赛时返回 true ,当 Bob 赢得比赛时返回 false 。
示例 1:
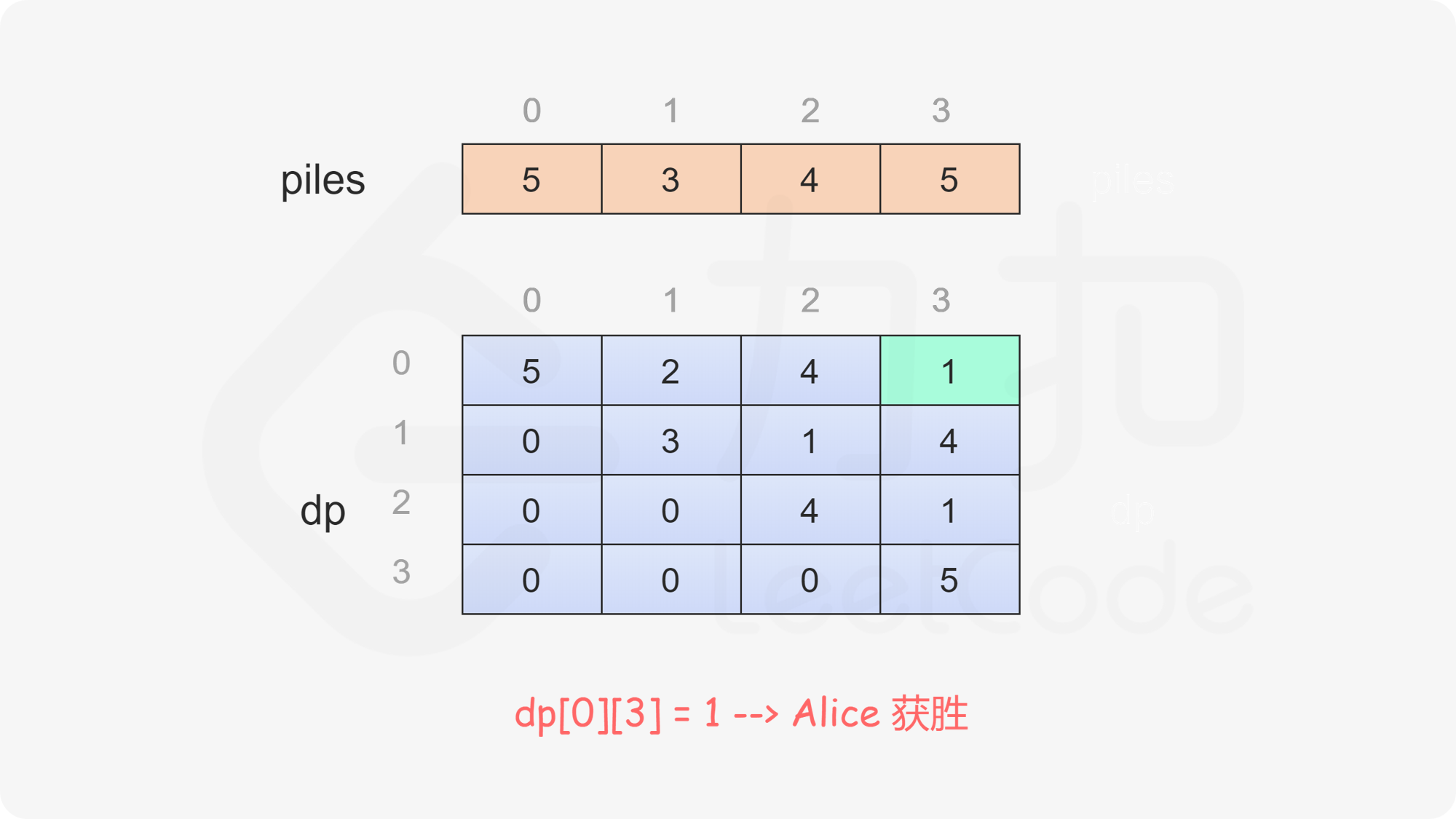
**输入:** piles = [5,3,4,5]
**输出:** true
**解释:**
Alice 先开始,只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗,这一行就变成了 [3,4,5] 。
如果 Bob 拿走前 3 颗,那么剩下的是 [4,5],Alice 拿走后 5 颗赢得 10 分。
如果 Bob 拿走后 5 颗,那么剩下的是 [3,4],Alice 拿走后 4 颗赢得 9 分。
这表明,取前 5 颗石子对 Alice 来说是一个胜利的举动,所以返回 true 。
示例 2:
**输入:** piles = [3,7,2,3]
**输出:** true
提示:
2 <= piles.length <= 500piles.length 是 偶数 1 <= piles[i] <= 500sum(piles[i]) 是 奇数
前言 这道题是「486. 预测赢家 」的特例。和第 486 题相比,这道题增加了两个限制条件:
数组的长度是偶数;
数组的元素之和是奇数,所以没有平局。
这道题可以使用第 486 题的解法进行求解。如果充分利用上述两个限制条件,还可以使用数学方法进行求解。
方法一:动态规划 由于每次只能从行的开始或结束处取走整堆石子,因此可以保证剩下的石子堆一定是连续的。
如果只剩下一堆石子,则当前玩家只能取走这堆石子。如果剩下多堆石子,则当前玩家可以选择从行的开始或结束处取走整堆石子,然后轮到另一个玩家在剩下的石子堆中取走石子。这是一个递归的过程,因此可以使用递归进行求解,递归过程中维护一个总数,表示 Alice 和 Bob 的石子数量之差,当游戏结束时,如果总数大于 0,则 Alice 赢得比赛,否则 Bob 赢得比赛。
如果有 n 堆石子,则递归的时间复杂度为 O(2^n),无法通过所有的测试用例。递归的时间复杂度高的原因是存在大量重复计算。由于存在重复子问题,因此可以使用动态规划降低时间复杂度。
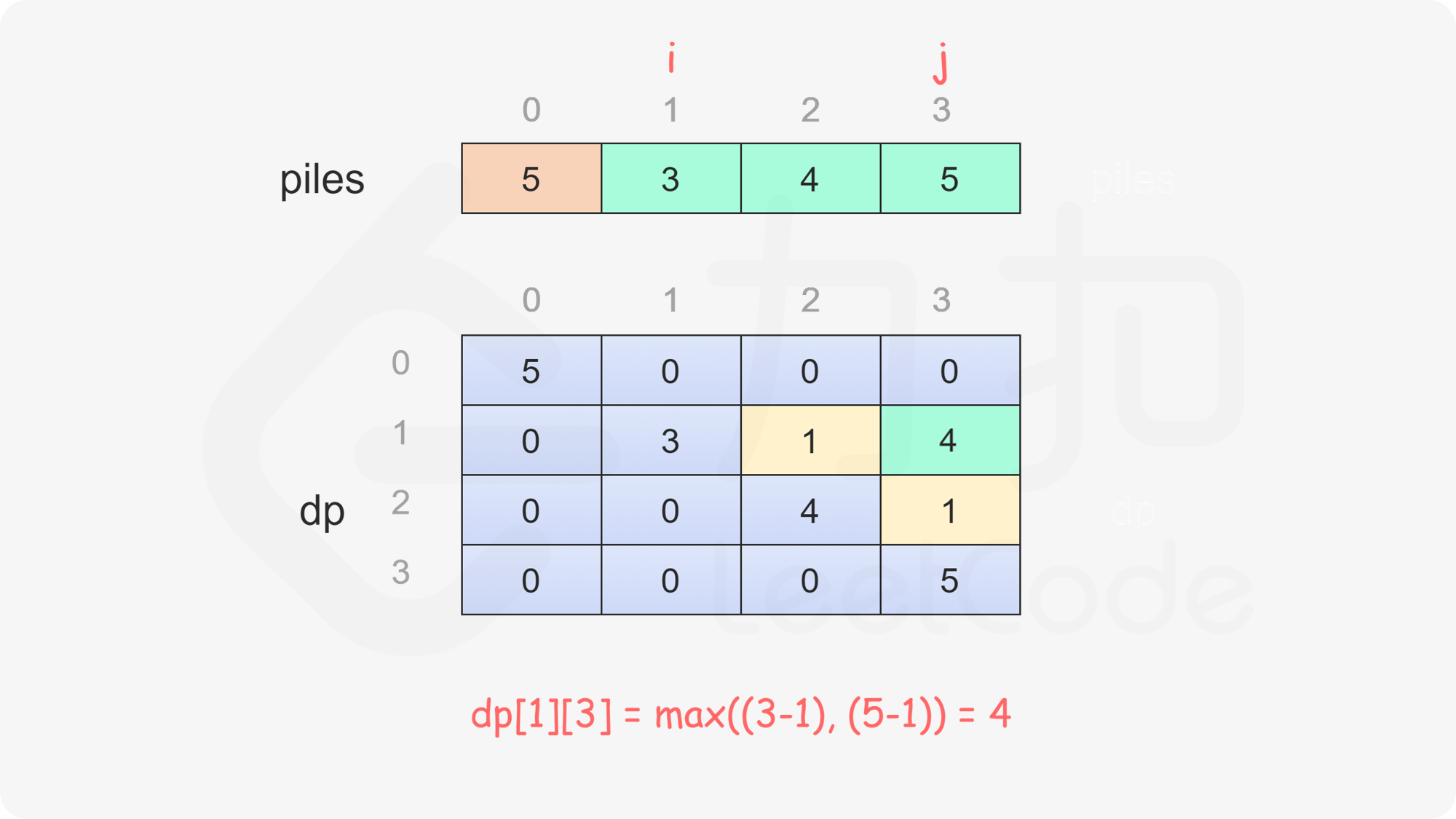
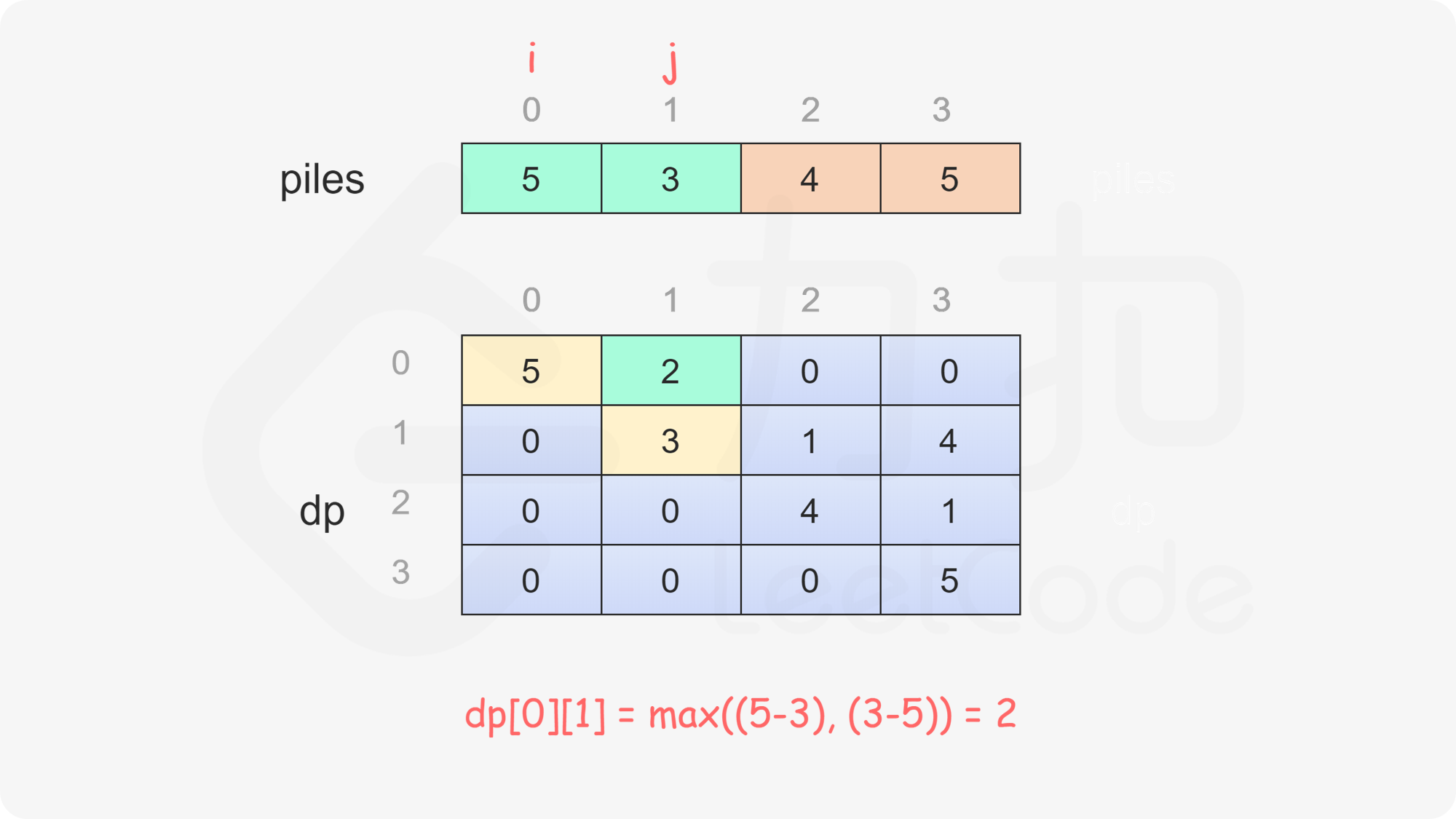
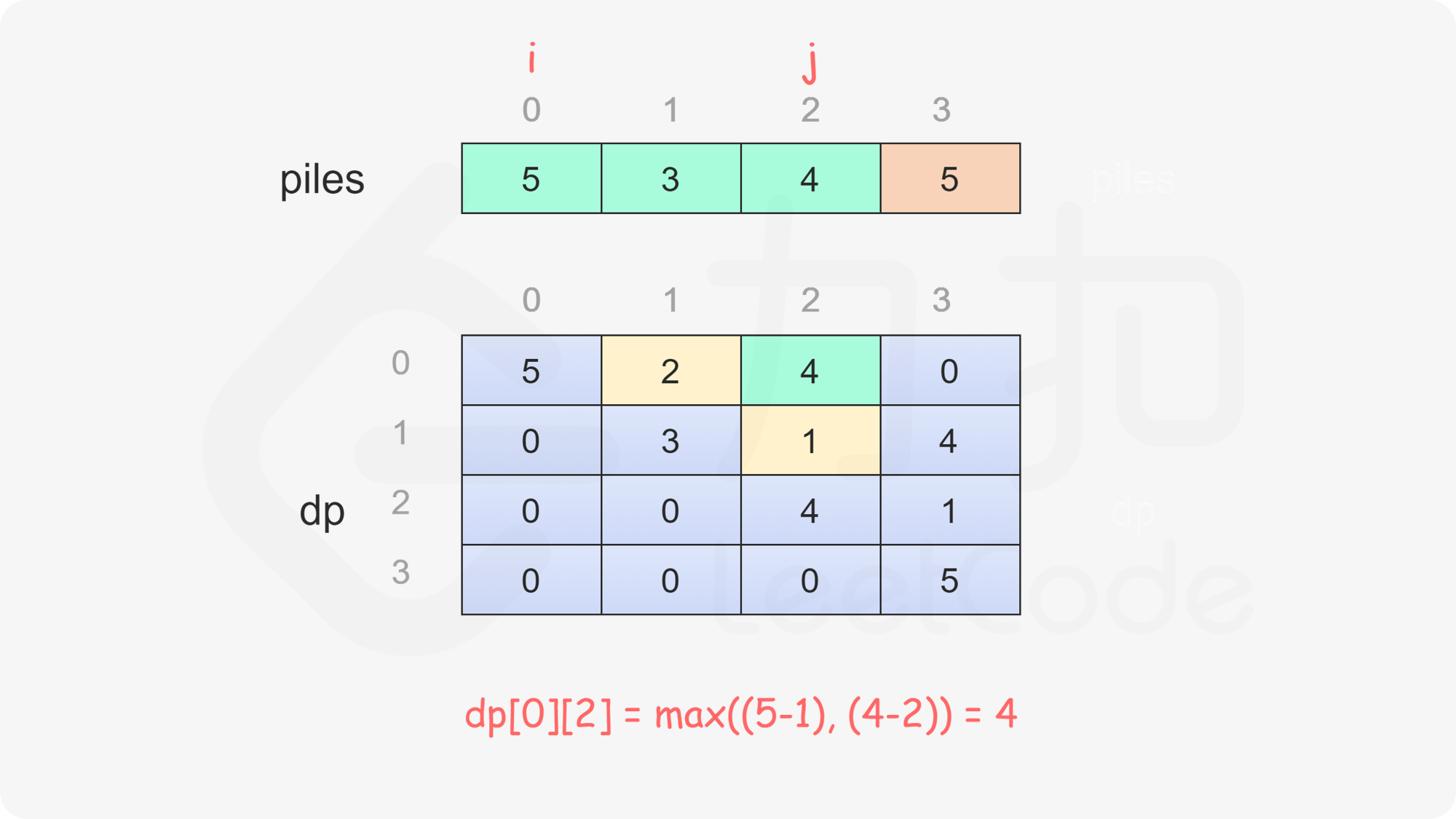
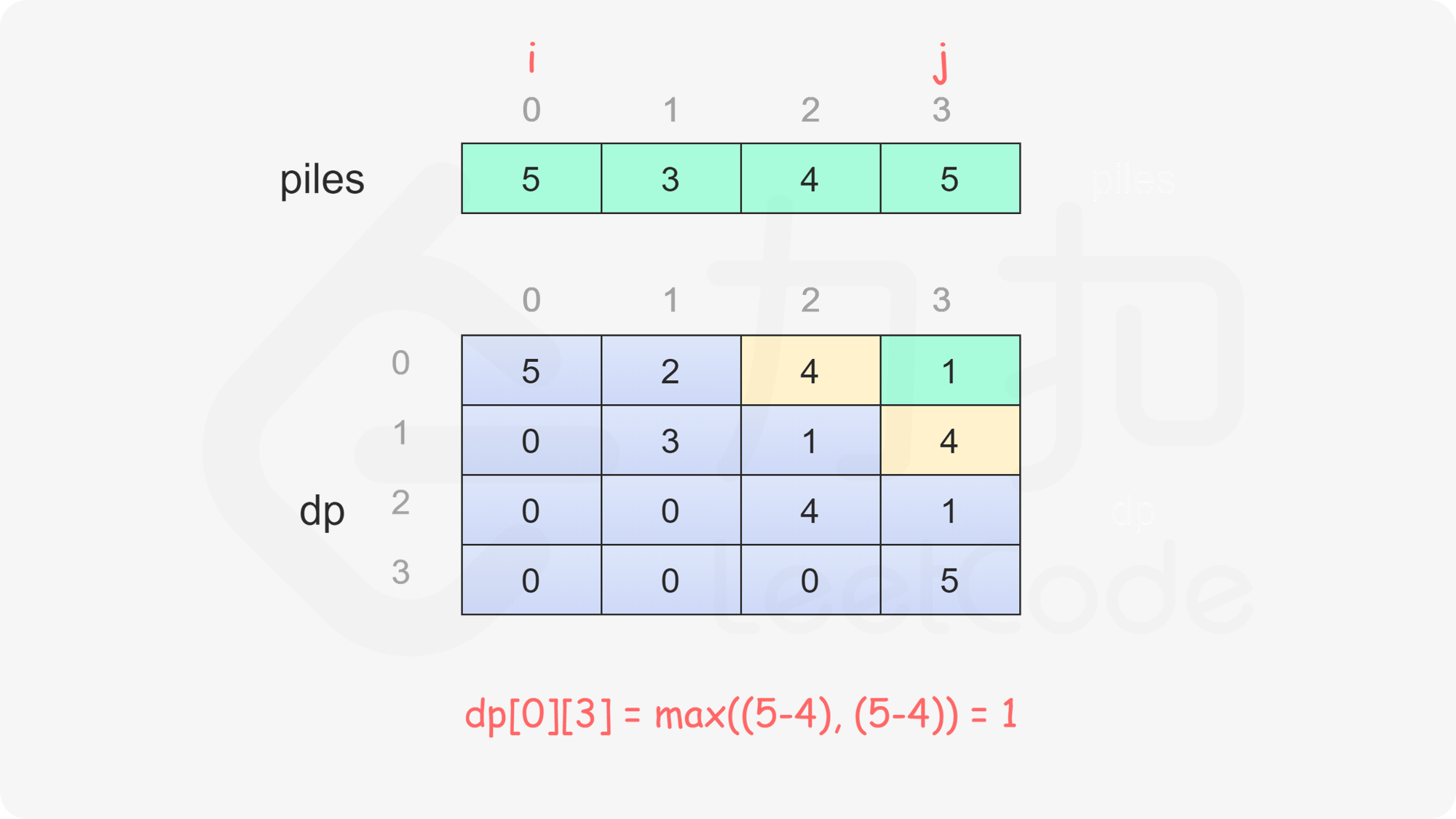
定义二维数组 dp,其行数和列数都等于石子的堆数,dp}[i][j] 表示当剩下的石子堆为下标 i 到下标 j 时,即在下标范围 [i, j] 中,当前玩家与另一个玩家的石子数量之差的最大值,注意当前玩家不一定是先手 Alice。
只有当 i \le j 时,剩下的石子堆才有意义,因此当 i>j 时,dp}[i][j]=0。
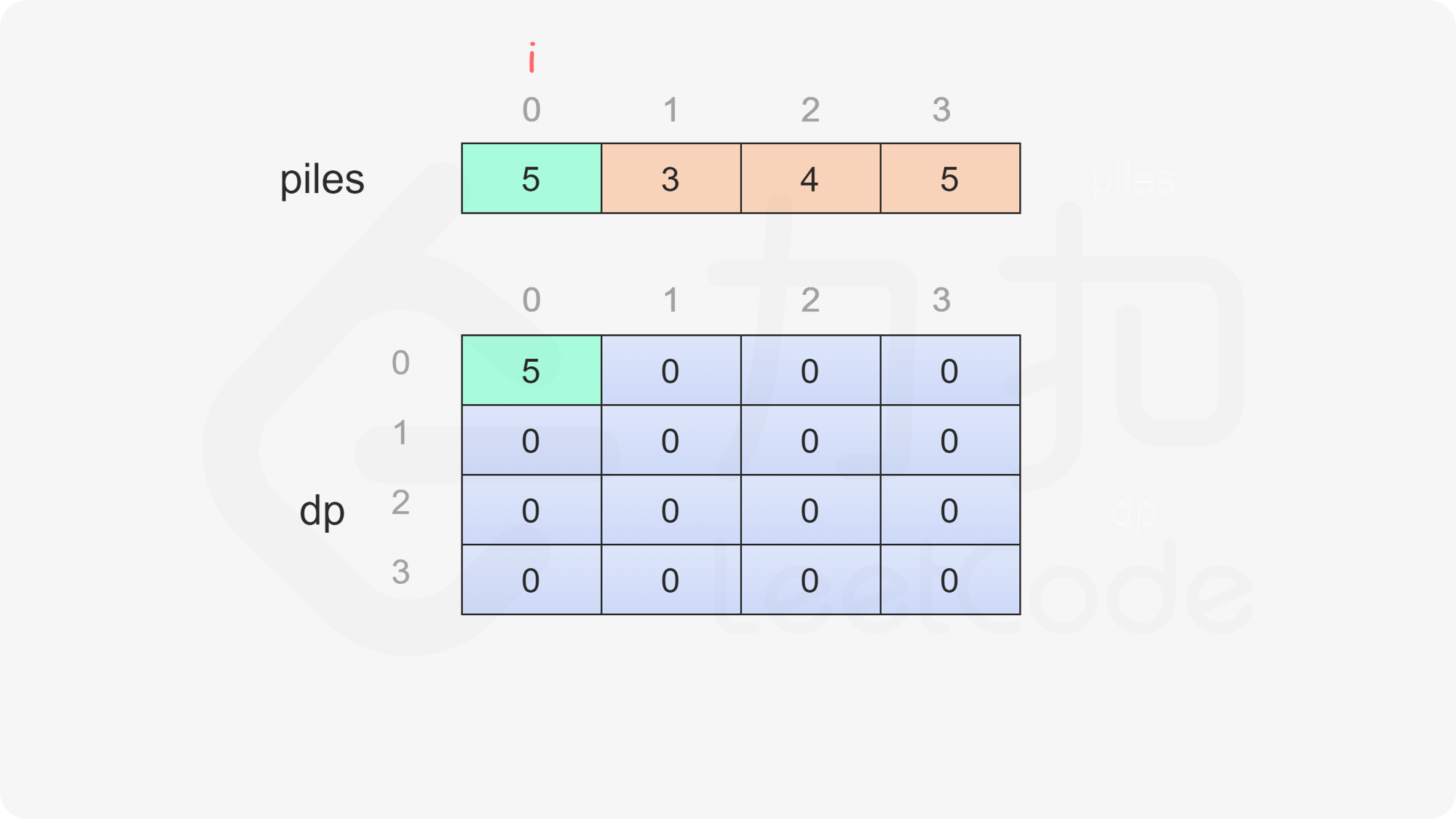
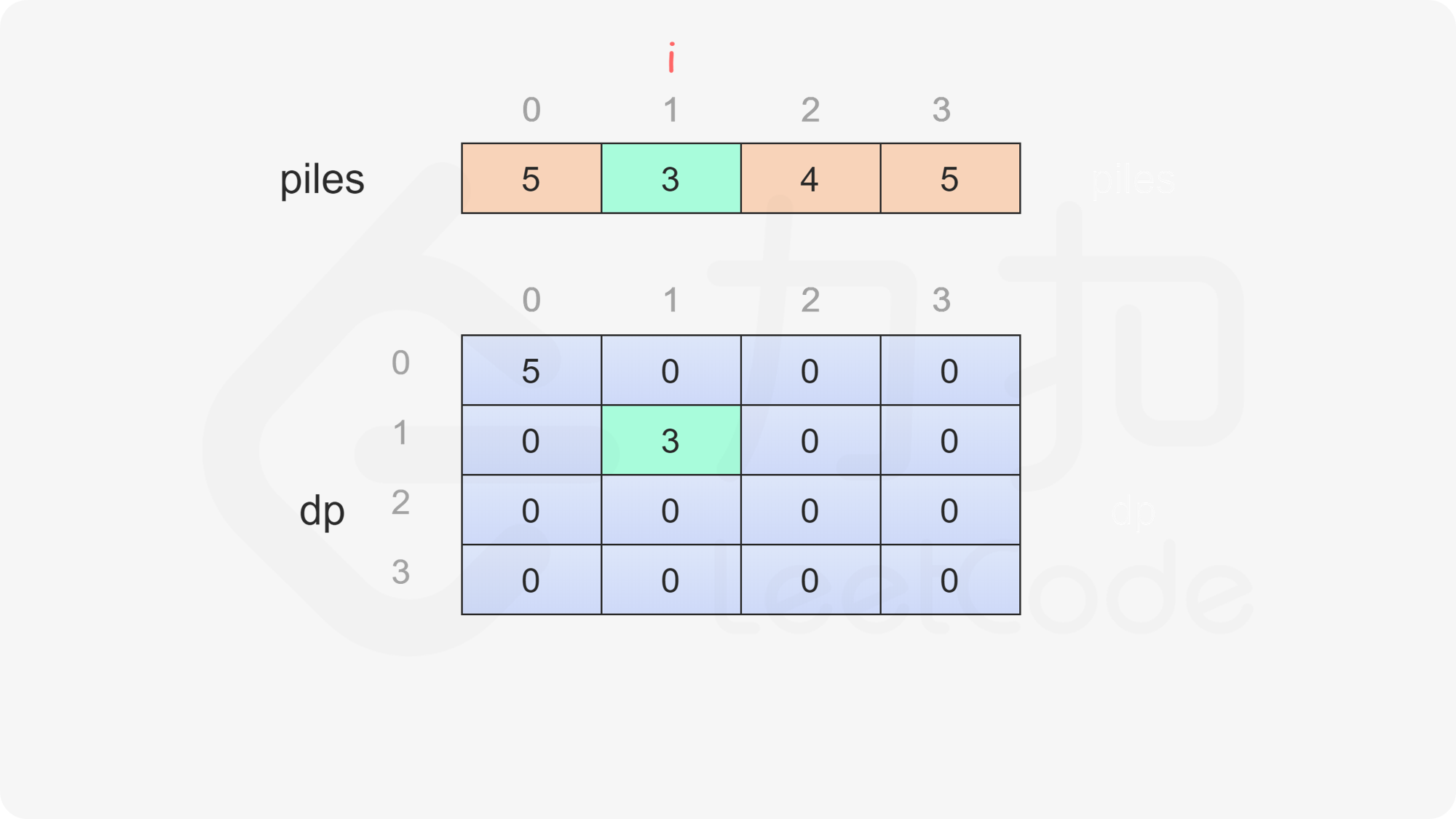
当 i=j 时,只剩下一堆石子,当前玩家只能取走这堆石子,因此对于所有 0 \le i < \textit{nums}.\text{length,都有 dp}[i][i]=\textit{piles}[i]。
当 i<j 时,当前玩家可以选择取走 piles}[i] 或 piles}[j],然后轮到另一个玩家在剩下的石子堆中取走石子。在两种方案中,当前玩家会选择最优的方案,使得自己的石子数量最大化。因此可以得到如下状态转移方程:
\textit{dp}[i][j]=\max(\textit{piles}[i] - \textit{dp}[i+1][j], \textit{piles}[j] - \textit{dp}[i][j-1])
最后判断 dp}[0][\textit{piles}.\text{length}-1] 的值,如果大于 0,则 Alice 的石子数量大于 Bob 的石子数量,因此 Alice 赢得比赛,否则 Bob 赢得比赛。
<
[sol11-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public boolean stoneGame (int [] piles) { int length = piles.length; int [][] dp = new int [length][length]; for (int i = 0 ; i < length; i++) { dp[i][i] = piles[i]; } for (int i = length - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < length; j++) { dp[i][j] = Math.max(piles[i] - dp[i + 1 ][j], piles[j] - dp[i][j - 1 ]); } } return dp[0 ][length - 1 ] > 0 ; } }
[sol11-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public class Solution { public bool StoneGame (int [] piles int length = piles.Length; int [,] dp = new int [length, length]; for (int i = 0 ; i < length; i++) { dp[i, i] = piles[i]; } for (int i = length - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < length; j++) { dp[i, j] = Math.Max(piles[i] - dp[i + 1 , j], piles[j] - dp[i, j - 1 ]); } } return dp[0 , length - 1 ] > 0 ; } }
[sol11-C] 1 2 3 4 5 6 7 8 9 10 11 12 bool stoneGame (int * piles, int pilesSize) { int dp[pilesSize][pilesSize]; for (int i = 0 ; i < pilesSize; i++) { dp[i][i] = piles[i]; } for (int i = pilesSize - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < pilesSize; j++) { dp[i][j] = fmax(piles[i] - dp[i + 1 ][j], piles[j] - dp[i][j - 1 ]); } } return dp[0 ][pilesSize - 1 ] > 0 ; }
[sol11-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : bool stoneGame (vector<int >& piles) int length = piles.size (); auto dp = vector<vector<int >>(length, vector <int >(length)); for (int i = 0 ; i < length; i++) { dp[i][i] = piles[i]; } for (int i = length - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < length; j++) { dp[i][j] = max (piles[i] - dp[i + 1 ][j], piles[j] - dp[i][j - 1 ]); } } return dp[0 ][length - 1 ] > 0 ; } };
[sol11-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 func stoneGame (piles []int ) bool { length := len (piles) dp := make ([][]int , length) for i := 0 ; i < length; i++ { dp[i] = make ([]int , length) dp[i][i] = piles[i] } for i := length - 2 ; i >= 0 ; i-- { for j := i + 1 ; j < length; j++ { dp[i][j] = max(piles[i] - dp[i+1 ][j], piles[j] - dp[i][j-1 ]) } } return dp[0 ][length-1 ] > 0 } func max (x, y int ) int { if x > y { return x } return y }
[sol11-Python3] 1 2 3 4 5 6 7 8 9 10 class Solution : def stoneGame (self, piles: List [int ] ) -> bool : length = len (piles) dp = [[0 ] * length for _ in range (length)] for i, pile in enumerate (piles): dp[i][i] = pile for i in range (length - 2 , -1 , -1 ): for j in range (i + 1 , length): dp[i][j] = max (piles[i] - dp[i + 1 ][j], piles[j] - dp[i][j - 1 ]) return dp[0 ][length - 1 ] > 0
[sol11-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 var stoneGame = function (piles ) { const length = piles.length ; const dp = new Array (length).fill (0 ).map (() => new Array (length).fill (0 )); for (let i = 0 ; i < length; i++) { dp[i][i] = piles[i]; } for (let i = length - 2 ; i >= 0 ; i--) { for (let j = i + 1 ; j < length; j++) { dp[i][j] = Math .max (piles[i] - dp[i + 1 ][j], piles[j] - dp[i][j - 1 ]); } } return dp[0 ][length - 1 ] > 0 ; };
上述代码中使用了二维数组 dp。分析状态转移方程可以看到,dp}[i][j] 的值只和 dp}[i + 1][j] 与 dp}[i][j - 1] 有关,即在计算 dp 的第 i 行的值时,只需要使用到 dp 的第 i 行和第 i+1 行的值,因此可以使用一维数组代替二维数组,对空间进行优化。
[sol12-Java] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Solution { public boolean stoneGame (int [] piles) { int length = piles.length; int [] dp = new int [length]; for (int i = 0 ; i < length; i++) { dp[i] = piles[i]; } for (int i = length - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < length; j++) { dp[j] = Math.max(piles[i] - dp[j], piles[j] - dp[j - 1 ]); } } return dp[length - 1 ] > 0 ; } }
[sol12-C#] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 public class Solution { public bool StoneGame (int [] piles int length = piles.Length; int [] dp = new int [length]; for (int i = 0 ; i < length; i++) { dp[i] = piles[i]; } for (int i = length - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < length; j++) { dp[j] = Math.Max(piles[i] - dp[j], piles[j] - dp[j - 1 ]); } } return dp[length - 1 ] > 0 ; } }
[sol12-C] 1 2 3 4 5 6 7 8 9 10 11 12 bool stoneGame (int * piles, int pilesSize) { int dp[pilesSize]; for (int i = 0 ; i < pilesSize; i++) { dp[i] = piles[i]; } for (int i = pilesSize - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < pilesSize; j++) { dp[j] = fmax(piles[i] - dp[j], piles[j] - dp[j - 1 ]); } } return dp[pilesSize - 1 ] > 0 ; }
[sol12-C++] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Solution {public : bool stoneGame (vector<int >& piles) int length = piles.size (); auto dp = vector <int >(length); for (int i = 0 ; i < length; i++) { dp[i] = piles[i]; } for (int i = length - 2 ; i >= 0 ; i--) { for (int j = i + 1 ; j < length; j++) { dp[j] = max (piles[i] - dp[j], piles[j] - dp[j - 1 ]); } } return dp[length - 1 ] > 0 ; } };
[sol12-Golang] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 func stoneGame (piles []int ) bool { length := len (piles) dp := make ([]int , length) for i := 0 ; i < length; i++ { dp[i] = piles[i] } for i := length - 2 ; i >= 0 ; i-- { for j := i + 1 ; j < length; j++ { dp[j] = max(piles[i] - dp[j], piles[j] - dp[j - 1 ]) } } return dp[length - 1 ] > 0 } func max (x, y int ) int { if x > y { return x } return y }
[sol12-Python3] 1 2 3 4 5 6 7 8 9 10 class Solution : def stoneGame (self, piles: List [int ] ) -> bool : length = len (piles) dp = [0 ] * length for i, pile in enumerate (piles): dp[i] = pile for i in range (length - 2 , -1 , -1 ): for j in range (i + 1 , length): dp[j] = max (piles[i] - dp[j], piles[j] - dp[j - 1 ]) return dp[length - 1 ] > 0
[sol12-JavaScript] 1 2 3 4 5 6 7 8 9 10 11 12 13 var stoneGame = function (piles ) { const length = piles.length ; const dp = new Array (length).fill (0 ); for (let i = 0 ; i < length; i++) { dp[i] = piles[i]; } for (let i = length - 2 ; i >= 0 ; i--) { for (let j = i + 1 ; j < length; j++) { dp[j] = Math .max (piles[i] - dp[j], piles[j] - dp[j - 1 ]); } } return dp[length - 1 ] > 0 ; };
复杂度分析
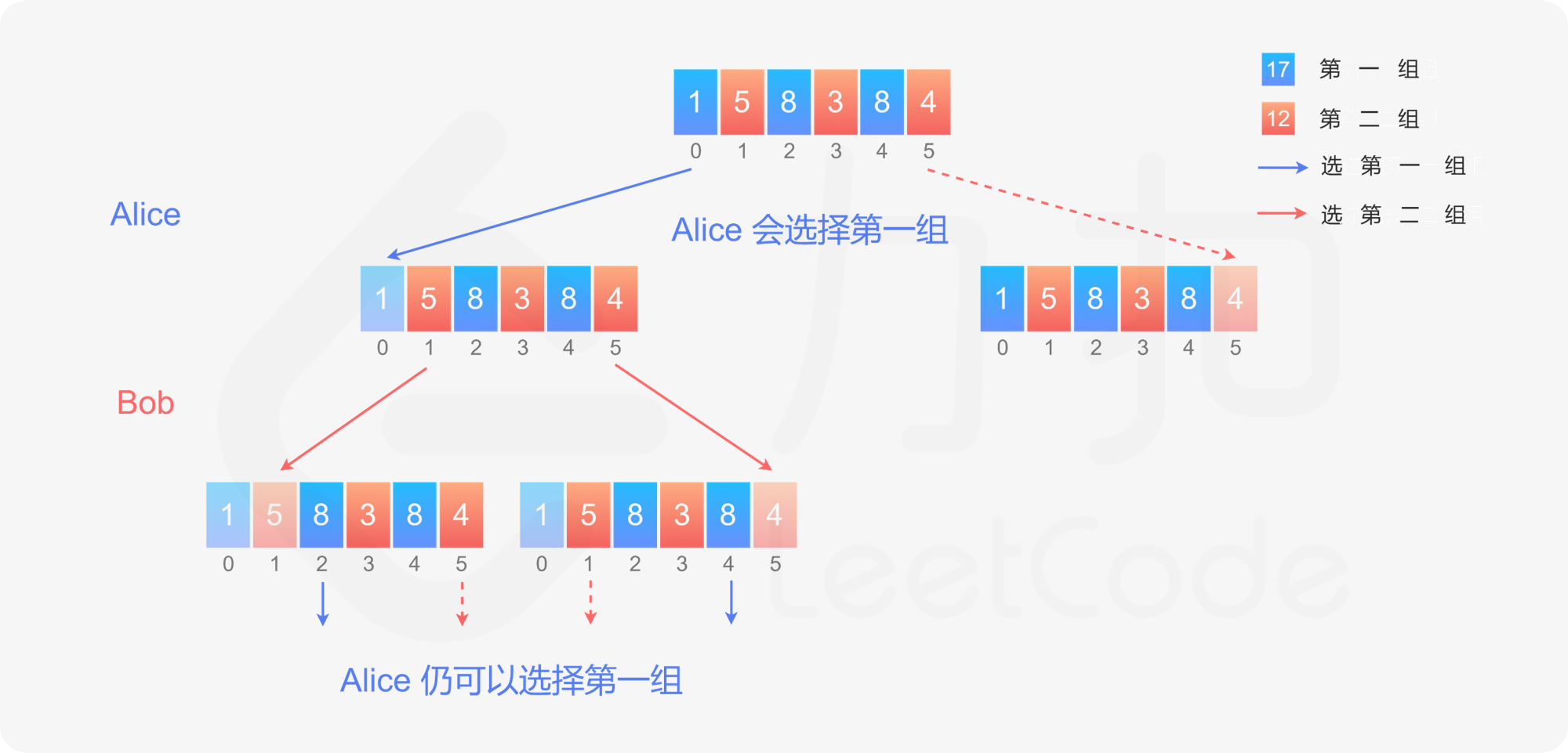
方法二:数学 假设有 n 堆石子,n 是偶数,则每堆石子的下标从 0 到 n-1。根据下标将 n 堆石子分成两组,每组有 n}{2 堆石子,下标为偶数的石子堆属于第一组,下标为奇数的石子堆属于第二组。
初始时,行的开始处的石子堆位于下标 0,属于第一组,行的结束处的石子堆位于下标 n-1,属于第二组,因此作为先手的 Alice 可以自由选择取走第一组的一堆石子或者第二组的一堆石子。如果 Alice 取走第一组的一堆石子,则剩下的部分在行的开始处和结束处的石子堆都属于第二组,因此 Bob 只能取走第二组的一堆石子。如果 Alice 取走第二组的一堆石子,则剩下的部分在行的开始处和结束处的石子堆都属于第一组,因此 Bob 只能取走第一组的一堆石子。无论 Bob 取走的是开始处还是结束处的一堆石子,剩下的部分在行的开始处和结束处的石子堆一定是属于不同组的,因此轮到 Alice 取走石子时,Alice 又可以在两组石子之间进行自由选择。
根据上述分析可知,作为先手的 Alice 可以在第一次取走石子时就决定取走哪一组的石子,并全程取走同一组的石子。既然如此,Alice 是否有必胜策略?
答案是肯定的。将石子分成两组之后,可以计算出每一组的石子数量,同时知道哪一组的石子数量更多。Alice 只要选择取走数量更多的一组石子即可。因此,Alice 总是可以赢得比赛。
[sol2-Java] 1 2 3 4 5 class Solution { public boolean stoneGame (int [] piles) { return true ; } }
[sol2-C#] 1 2 3 4 5 public class Solution { public bool StoneGame (int [] piles return true ; } }
[sol2-C] 1 2 3 bool stoneGame (int * piles, int pilesSize) { return true ; }
[sol2-C++] 1 2 3 4 5 6 class Solution {public : bool stoneGame (vector<int >& piles) return true ; } };
[sol2-Golang] 1 2 3 func stoneGame (piles []int ) bool { return true }
[sol2-Python3] 1 2 3 class Solution : def stoneGame (self, piles: List [int ] ) -> bool : return True
[sol2-JavaScript] 1 2 3 var stoneGame = function (piles ) { return true ; };
复杂度分析
 ,
, ,
, ,
,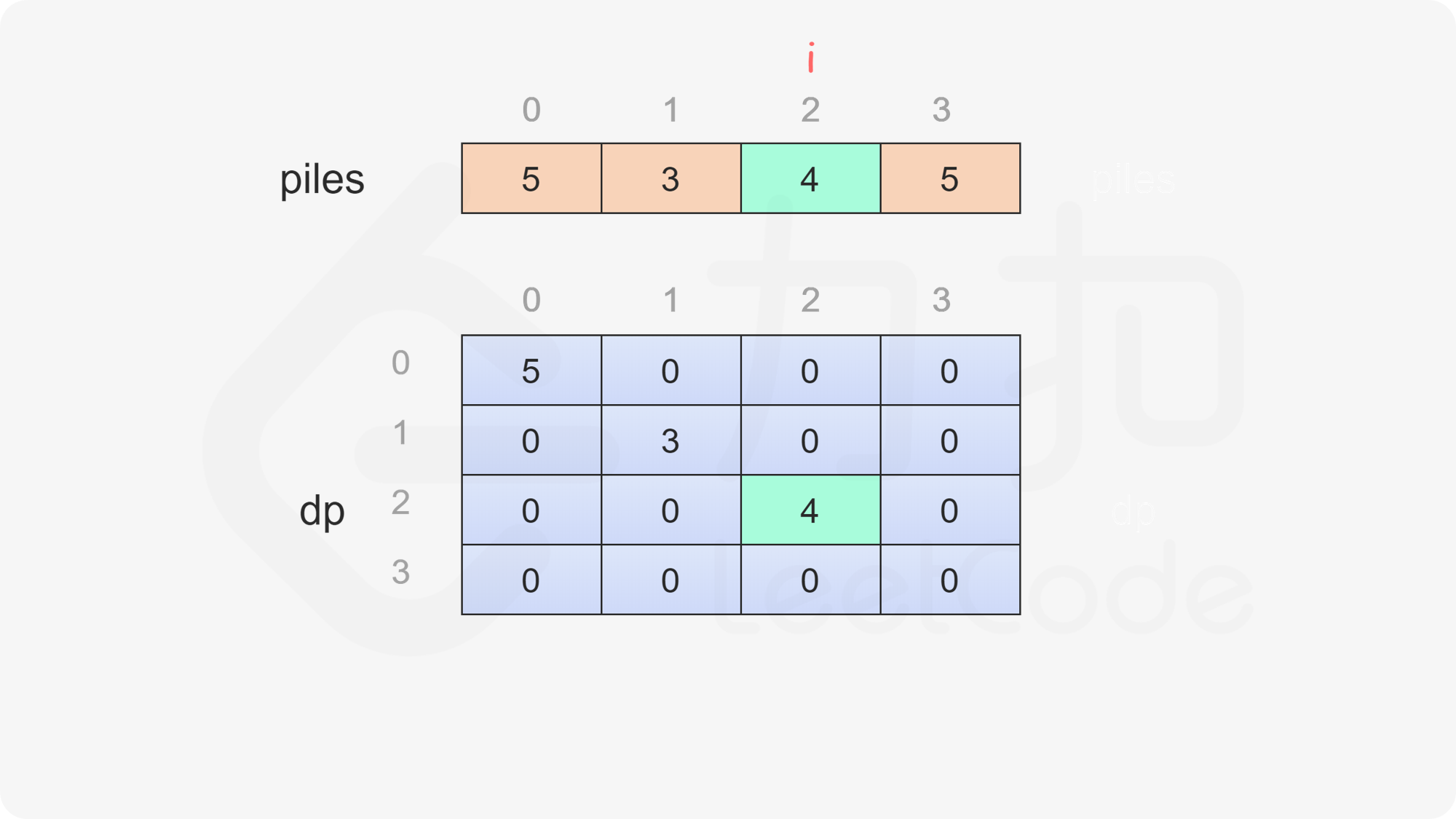 ,
,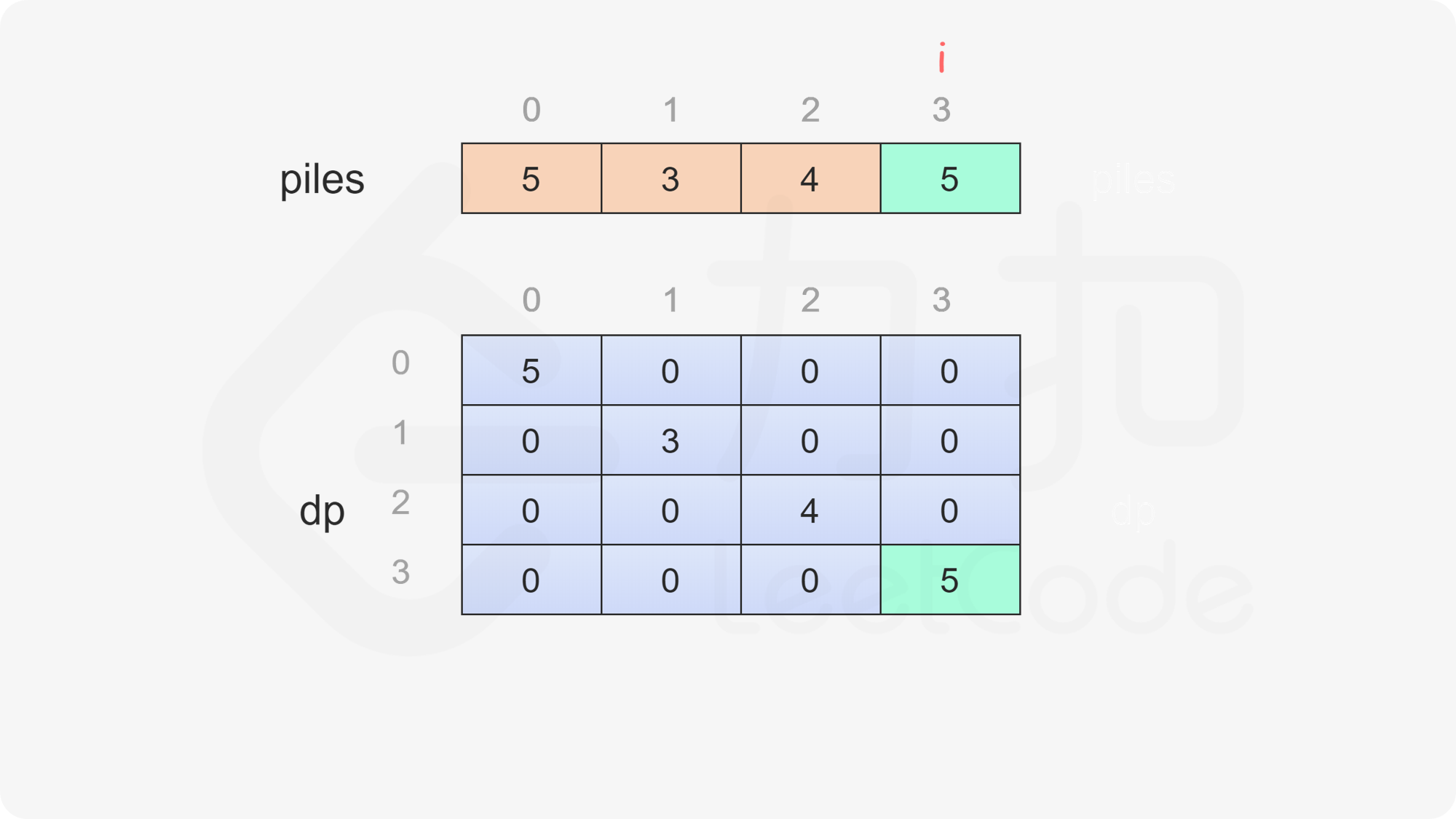 ,
,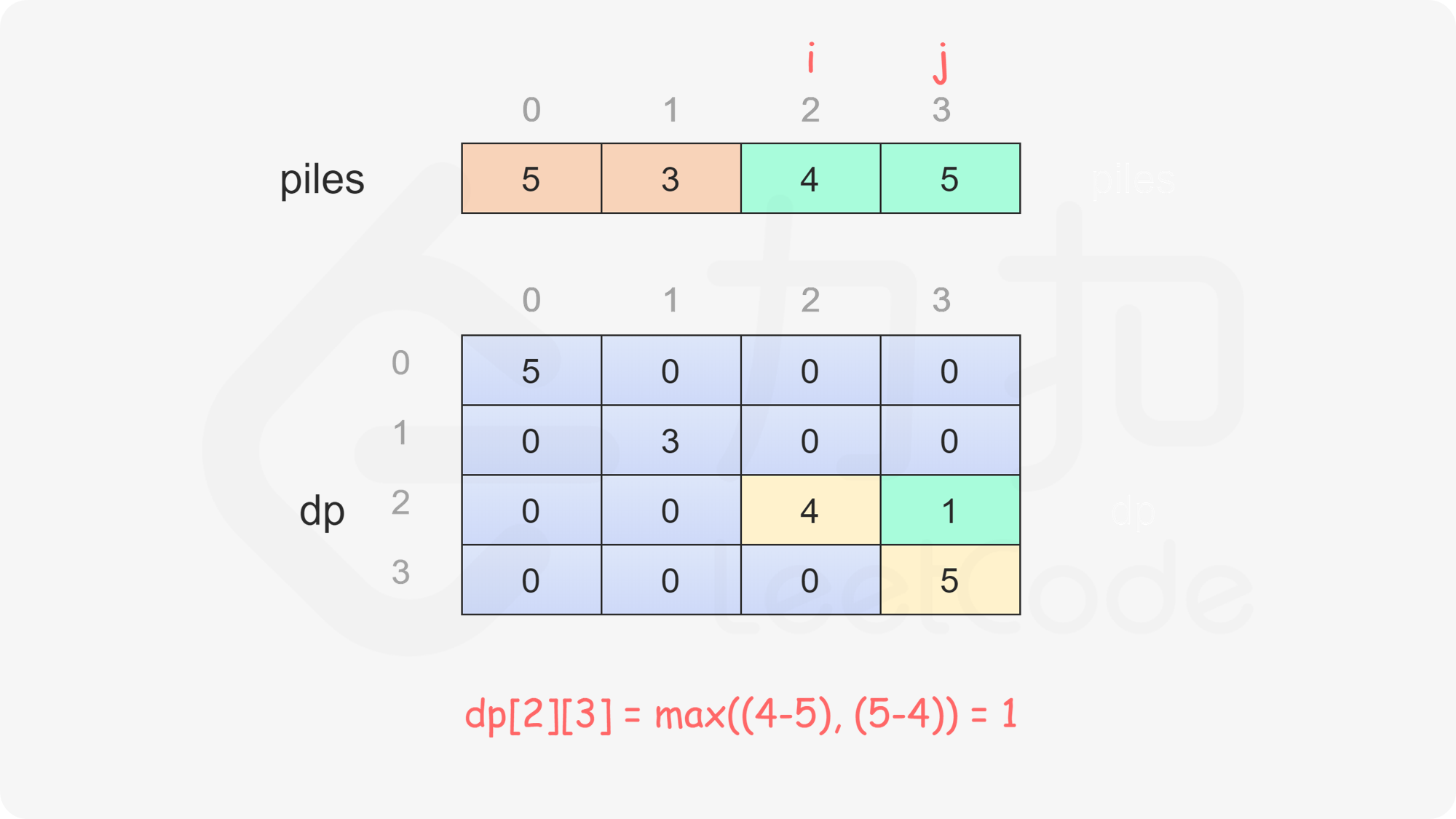 ,
,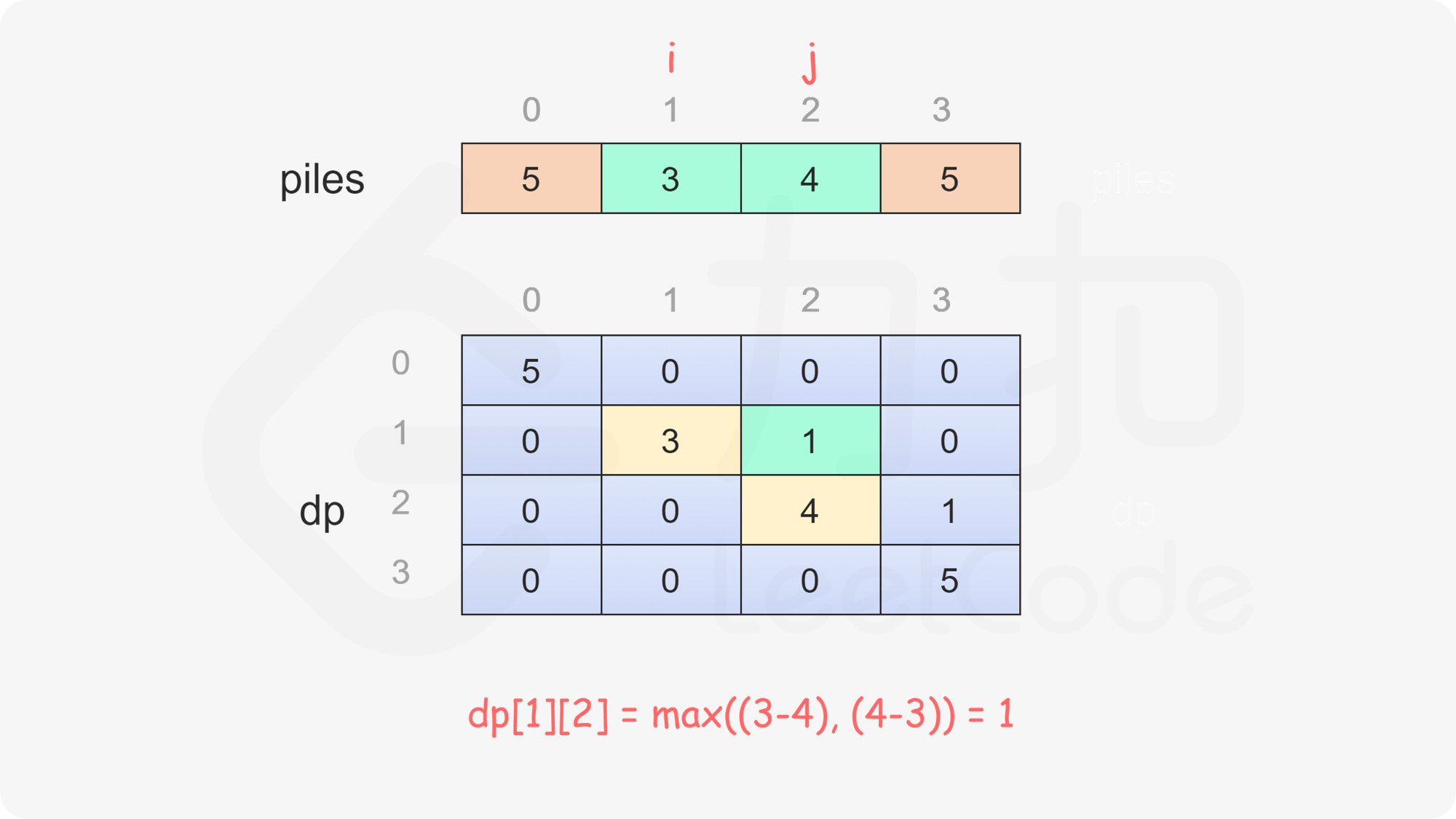 ,
, ,
, ,
, ,
, ,
, >
>