0885-螺旋矩阵 III

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

在 rows x cols 的网格上，你从单元格 (rStart, cStart)
面朝东面开始。网格的西北角位于第一行第一列，网格的东南角位于最后一行最后一列。

你需要以顺时针按螺旋状行走，访问此网格中的每个位置。每当移动到网格的边界之外时，需要继续在网格之外行走（但稍后可能会返回到网格边界）。

最终，我们到过网格的所有 rows x cols 个空间。

按照访问顺序返回表示网格位置的坐标列表。

示例 1：

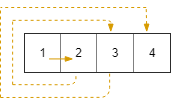
**输入：** rows = 1, cols = 4, rStart = 0, cStart = 0
**输出：** [[0,0],[0,1],[0,2],[0,3]]

示例 2：

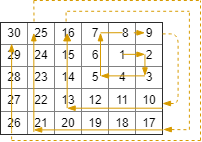
**输入：** rows = 5, cols = 6, rStart = 1, cStart = 4
**输出：** [[1,4],[1,5],[2,5],[2,4],[2,3],[1,3],[0,3],[0,4],[0,5],[3,5],[3,4],[3,3],[3,2],[2,2],[1,2],[0,2],[4,5],[4,4],[4,3],[4,2],[4,1],[3,1],[2,1],[1,1],[0,1],[4,0],[3,0],[2,0],[1,0],[0,0]]

提示：

  • 1 <= rows, cols <= 100
  • 0 <= rStart < rows
  • 0 <= cStart < cols

方法：螺旋形行走

思路

我们可以从开始的正方形开始，以螺旋形的形状行走，而忽略我们是否呆在网格中。最终，我们一定已经到达了网格的每一个角落。

算法

检查我们在每个方向的行走长度，我们发现如下模式：1，1，2，2，3，3，4，4，... 即我们先向东走 1 单位，然后向南走 1 单位，再向西走 2 单位，再向北走 2 单位，再向东走 3 单位，等等。因为我们的行走方式是自相似的，所以这种模式会以我们期望的方式重复。

之后，算法很简单：按照我们访问的顺序执行遍历并记录网格的位置。有关更多细节，请阅读内联注释。

[ZbnuoMgN-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int[][] spiralMatrixIII(int R, int C, int r0, int c0) {
        int[] dr = new int[]{0, 1, 0, -1};
        int[] dc = new int[]{1, 0, -1, 0};

        int[][] ans = new int[R*C][2];
        int t = 0;

        ans[t++] = new int[]{r0, c0};
        if (R * C == 1) return ans;

        for (int k = 1; k < 2*(R+C); k += 2)
            for (int i = 0; i < 4; ++i) {  // i: direction index
                int dk = k + (i / 2);  // number of steps in this direction
                for (int j = 0; j < dk; ++j) {  // for each step in this direction...
                    // step in the i-th direction
                    r0 += dr[i];
                    c0 += dc[i];
                    if (0 <= r0 && r0 < R && 0 <= c0 && c0 < C) {
                        ans[t++] = new int[]{r0, c0};
                        if (t == R * C) return ans;
                    }
                }
            }

        throw null;
    }
}
[ZbnuoMgN-Python]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution(object):
    def spiralMatrixIII(self, R, C, r0, c0):
        ans = [(r0, c0)]
        if R * C == 1: return ans

        # For walk length k = 1, 3, 5 ...
        for k in xrange(1, 2*(R+C), 2):

            # For direction (dr, dc) = east, south, west, north;
            # and walk length dk...
            for dr, dc, dk in ((0, 1, k), (1, 0, k), (0, -1, k+1), (-1, 0, k+1)):

                # For each of dk units in the current direction ...
                for _ in xrange(dk):
                    # Step in that direction
                    r0 += dr
                    c0 += dc

                    # If on the grid ...
                    if 0 <= r0 < R and 0 <= c0 < C:
                        ans.append((r0, c0))
                        if len(ans) == R * C:
                            return ans

复杂度分析

  • 时间复杂度：O((\max(R, C))^2)，潜在地，我们的行走需要螺旋式行进，直到我们向一个方向移动 R，向另一个方向移动 C，以便到达网格的每个单元格。

  • 空间复杂度：O(R * C)，答案用去的空间。

 Comments
On this page
0885-螺旋矩阵 III