0887-鸡蛋掉落
给你 k 枚相同的鸡蛋,并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。
已知存在楼层 f ,满足 0 <= f <= n ,任何从 高于 f 的楼层落下的鸡蛋都会碎,从 f
楼层或比它低的楼层落下的鸡蛋都不会破。
每次操作,你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下(满足 1 <= x <= n)。如果鸡蛋碎了,你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎,则可以在之后的操作中 重复使用 这枚鸡蛋。
请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少?
示例 1:
**输入:** k = 1, n = 2
**输出:** 2
**解释:**
鸡蛋从 1 楼掉落。如果它碎了,肯定能得出 f = 0 。
否则,鸡蛋从 2 楼掉落。如果它碎了,肯定能得出 f = 1 。
如果它没碎,那么肯定能得出 f = 2 。
因此,在最坏的情况下我们需要移动 2 次以确定 f 是多少。
示例 2:
**输入:** k = 2, n = 6
**输出:** 3
示例 3:
**输入:** k = 3, n = 14
**输出:** 4
提示:
1 <= k <= 1001 <= n <= 104
📺 视频题解
📖 文字题解
前言
本题是谷歌的一道经典面试题。由于本题过于经典,谷歌公司已经不再将这题作为面试的候选题目了。
本题难度较高,要想通过本题,需要一定的动态规划优化或数学功底。本题的标准解法为动态规划,由于篇幅有限,不会叙述 动态规划的边界条件、自底向上的动态规划和自顶向下的动态规划分别怎么实现 等较为基础的知识,而是把重点放在推导动态规划状态转移方程的过程,以及优化的思路、证明以及方法。
读者应当期望在阅读完本题解后,能够对方法一有一个大致的思路,并且可以在尝试中编写出代码。方法一已经是很优秀的解法,本题解也着重于此。而对于方法二和方法三,已经超过了面试难度,是竞赛中的考点,仅供读者挑战自我的极限。
方法一:动态规划 + 二分查找
思路和算法
我们可以考虑使用动态规划来做这道题,状态可以表示成 (k, n),其中 k 为鸡蛋数,n 为楼层数。当我们从第 x 楼扔鸡蛋的时候:
如果鸡蛋不碎,那么状态变成 (k, n-x),即我们鸡蛋的数目不变,但答案只可能在上方的 n-x 层楼了。也就是说,我们把原问题缩小成了一个规模为 (k, n-x) 的子问题;
如果鸡蛋碎了,那么状态变成 (k-1, x-1),即我们少了一个鸡蛋,但我们知道答案只可能在第 x 楼下方的 x-1 层楼中了。也就是说,我们把原问题缩小成了一个规模为 (k-1, x-1) 的子问题。
这样一来,我们定义 dp}(k, n) 为在状态 (k, n) 下最少需要的步数。根据以上分析我们可以列出状态转移方程:
\textit{dp}(k, n) = 1 + \min\limits_{1 \leq x \leq n} \Big( \max(\textit{dp}(k-1, x-1), \textit{dp}(k, n-x)) \Big)
这个状态转移方程是如何得来的呢?对于 dp}(k, n) 而言,我们像上面分析的那样,枚举第一个鸡蛋扔在的楼层数 x。由于我们并不知道真正的 f 值,因此我们必须保证 鸡蛋碎了之后接下来需要的步数 和 鸡蛋没碎之后接下来需要的步数 二者的 最大值 最小,这样就保证了在 最坏情况下(也就是无论 f 的值如何) dp}(k, n) 的值最小。如果能理解这一点,也就能理解上面的状态转移方程,即最小化 \max(\textit{dp}(k-1, x-1), \textit{dp}(k, n-x))。
如果我们直接暴力转移求解每个状态的 dp 值,时间复杂度是为 O(kn^2),即一共有 O(kn) 个状态,对于每个状态枚举扔鸡蛋的楼层 x,需要 O(n) 的时间。这无疑在当前数据范围下是会超出时间限制的,因此我们需要想办法优化枚举的时间复杂度。
我们观察到 dp}(k, n) 是一个关于 n 的单调递增函数,也就是说在鸡蛋数 k 固定的情况下,楼层数 n 越多,需要的步数一定不会变少。在上述的状态转移方程中,第一项 \mathcal{T_1}(x) = \textit{dp}(k-1, x-1) 是一个随 x 的增加而单调递增的函数,第二项 \mathcal{T_2}(x) = \textit{dp}(k, n-x) 是一个随着 x 的增加而单调递减的函数。
这如何帮助我们来优化这个问题呢?当 x 增加时,\mathcal{T_1}(x) 单调递增而 \mathcal{T_2}(x) 单调递减,我们可以想象在一个直角坐标系中,横坐标为 x,纵坐标为 \mathcal{T_1}(x) 和 \mathcal{T_2}(x)。当一个函数单调递增而另一个函数单调递减时,我们如何找到一个位置使得它们的最大值最小呢?
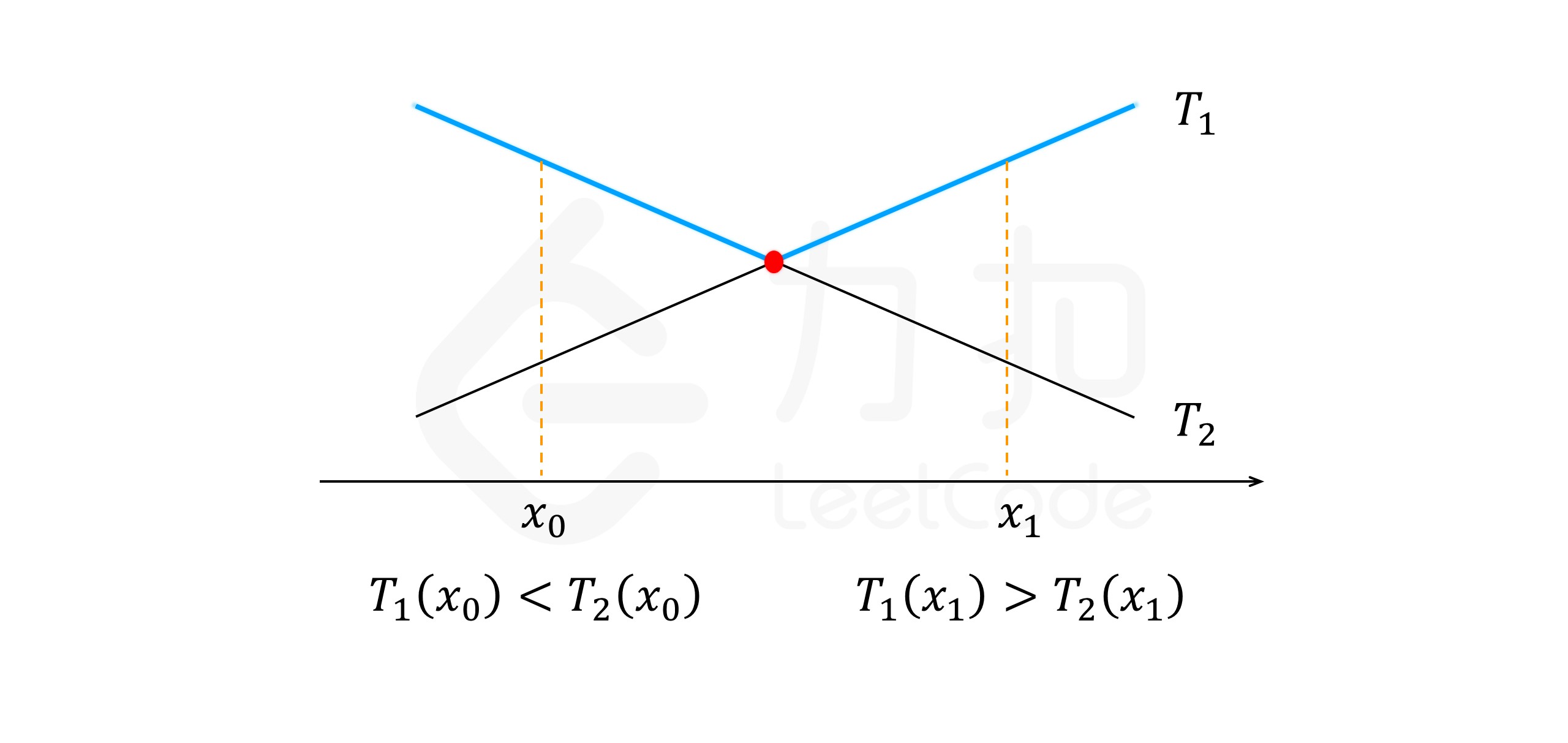
如上图所示,如果这两个函数都是连续函数,那么我们只需要找出这两个函数的交点,在交点处就能保证这两个函数的最大值最小。但在本题中,\mathcal{T_1}(x) 和 \mathcal{T_2}(x) 都是离散函数,也就是说,x 的值只能取 1, 2, 3 等等。在这种情况下,我们需要找到最大的满足 \mathcal{T_1}(x) < \mathcal{T_2}(x) 的 x_0,以及最小的满足 \mathcal{T_1}(x) \geq \mathcal{T_2}(x) 的 x_1,对应到上图中,就是离这两个函数(想象中的)交点左右两侧最近的整数。
我们只需要比较在 x_0 和 x_1 处两个函数的最大值,取一个最小的作为 x 即可。在数学上,我们可以证明出 x_0 和 x_1 相差 1,这也是比较显然的,因为它们正好夹住了那个想象中的交点,并且相距尽可能地近。因此我们就可以使用二分查找的方法找出 x_0,再得到 x_1:
我们在所有满足条件的 x 上进行二分查找。对于状态 (k, n) 而言,x 即为 [1, n] 中的任一整数;
在二分查找的过程中,假设当前这一步我们查找到了 x_\textit{mid,如果 \mathcal{T_1}(x_\textit{mid}) > \mathcal{T_2}(x_\textit{mid}),那么真正的 x_0 一定在 x_\textit{mid 的左侧,否则真正的 x_0 在 x_\textit{mid 的右侧。
二分查找的写法因人而异,本质上我们就是需要找到最大的满足 \mathcal{T_1}(x) < \mathcal{T_2}(x) 的 x_0,根据 x_\textit{mid 进行二分边界的调整。在得到了 x_0 后,我们可以知道 x_1 即为 x_0 + 1,此时我们只需要比较 \max(\mathcal{T_1}(x_0), \mathcal{T_2}(x_0)) 和 \max(\mathcal{T_1}(x_1), \mathcal{T_2}(x_1)),取较小的那个对应的位置作为 x 即可。
这样一来,对于给定的状态 (k, n),我们只需要 O(\log n) 的时间,通过二分查找就能得到最优的那个 x,因此时间复杂度从 O(kn^2) 降低至 O(kn \log n),可以通过本题。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:O(kn \log n)。我们需要计算 O(kn) 个状态,每个状态计算时需要 O(\log n) 的时间进行二分查找。
空间复杂度:O(kn)。我们需要 O(kn) 的空间存储每个状态的解。
方法二:决策单调性
说明
方法二涉及决策单调性,是竞赛中的考点。这里我们不会叙述 何为决策单调性 以及 如何根据决策单调性写出优化的动态规划,而是仅指出决策单调性的存在性。
思路
我们重新写下方法一中的状态转移方程:
dp(k, n) = 1 + \min\limits_{1 \leq x \leq n} \Big( \max(dp(k-1, x-1), dp(k, n-x)) \Big)
并且假设 x_\textit{opt 是使得 dp(k, n) 取到最优值的最小决策点 x_0。
x_\textit{opt} = \arg \min\limits_{1 \leq x \leq n} \Big( \max(dp(k-1, x-1), dp(k, n-x)) \Big)
在方法一中,我们是通过二分查找的方法,找到 x_0 和 x_1 中最优的作为 x_\textit{opt 的,那么还有什么更好的方法吗?
我们固定 k,随着 n 的增加,对于状态转移方程中 dp(k-1, x-1) 这一项,它的值是不变的,因为它和 n 无关。而对于状态转移方程中 dp(k, n-x) 这一项,随着 n 的增加,它的值也会增加。在方法一中,我们知道 dp(k-1, x-1) 随着 x 单调递增,而 dp(k, n-x) 随着 x 单调递减,那么当 n 增加时,dp(k, n-x) 对应的函数折线图在每个整数点上都是增加的,因此在 dp(k-1, x-1) 不变的情况下,x_\textit{opt 是单调递增的。
我们可以想象一条斜率为负的直线和一条斜率为正的直线,当斜率为负的直线(类比 dp(k, n-x))向上平移(类比 n 的增加)时,它和斜率为正的直线(类比 dp(k-1, x-1))的交点会一直向右移动,这个交点就确定了 x_\textit{opt,这与方法一也是一致的。
因此当我们固定 k 时,随着 n 的增加,dp(k, n) 对应的最优解的坐标 x_\textit{opt 单调递增,这样一来每个 dp(k, n) 的均摊时间复杂度为 O(1)。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:O(kn)。我们需要计算 O(kn) 个状态,同时对于每个 k,最优解指针只会从 0 到 n 走一次,复杂度也是 O(kn)。因此总体复杂度为 O(kn)。
空间复杂度:O(n)。因为 dp 每一层的解只依赖于上一层的解,因此我们每次只保留一层的解,需要的空间复杂度为 O(n)。
方法三:数学法
说明
方法三涉及逆向思维,是一种没见过就不太可能想出来,读过题解也很容易忘记的方法。
思路
反过来想这个问题:如果我们可以做 t 次操作,而且有 k 个鸡蛋,那么我们能找到答案的最高的 n 是多少?我们设 f(t, k) 为在上述条件下的 n。如果我们求出了所有的 f(t, k),那么只需要找出最小的满足 f(t, k) \geq n 的 t。
那么我们如何求出 f(t, k) 呢?我们还是使用动态规划。因为我们需要找出最高的 n,因此我们不必思考到底在哪里扔这个鸡蛋,我们只需要扔出一个鸡蛋,看看到底发生了什么:
如果鸡蛋没有碎,那么对应的是 f(t - 1, k),也就是说在这一层的上方可以有 f(t - 1, k) 层;
如果鸡蛋碎了,那么对应的是 f(t - 1, k - 1),也就是说在这一层的下方可以有 f(t - 1, k - 1) 层。
因此我们就可以写出状态转移方程:
f(t, k) = 1 + f(t-1, k-1) + f(t-1, k)
边界条件为:当 t \geq 1 的时候 f(t, 1) = t,当 k \geq 1 时,f(1, k) = 1。
那么问题来了:t 最大可以达到多少?由于我们在进行动态规划时,t 在题目中并没有给出,那么我们需要进行到动态规划的哪一步呢?可以发现,操作次数是一定不会超过楼层数的,因此 t \leq n,我们只要算出在 f(n, k) 内的所有 f 值即可。
1 | class Solution { |
1 | class Solution: |
1 | class Solution { |
复杂度分析
时间复杂度:O(kn)。事实上,更准确的时间复杂度应当为 O(kt),我们不加证明地给出 n = O(t^k),因此有 O(kt) = O(k\sqrt[k]{n})。
空间复杂度:O(kn)。
