0894-所有可能的真二叉树
给你一个整数 n ,请你找出所有可能含 n 个节点的 真二叉树 ,并以列表形式返回。答案中每棵树的每个节点都必须符合 Node.val == 0 。
答案的每个元素都是一棵真二叉树的根节点。你可以按 任意顺序 返回最终的真二叉树列表 。
真二叉树 是一类二叉树,树中每个节点恰好有 0 或 2 个子节点。
示例 1:
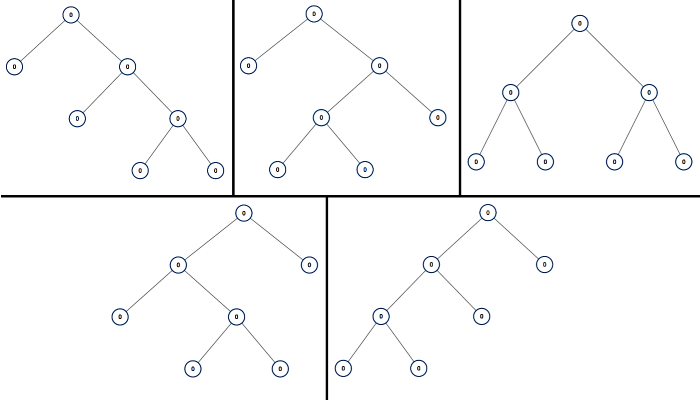
**输入:** n = 7
**输出:** [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
示例 2:
**输入:** n = 3
**输出:** [[0,0,0]]
提示:
1 <= n <= 20
方法:递归
思路与算法
令 FBT}(N) 作为所有含 N 个结点的可能的满二叉树的列表。
每个满二叉树 T 含有 3 个或更多结点,在其根结点处有 2 个子结点。这些子结点 left 和 right 本身就是满二叉树。
因此,对于 N \geq 3,我们可以设定如下的递归策略:FBT}(N) = [对于所有的 x,所有的树的左子结点来自 FBT}(x) 而右子结点来自 FBT}(N-1-x)]。
此外,通过简单的计数参数,没有满二叉树具有正偶数个结点。
最后,我们应该缓存函数 FBT 之前的结果,这样我们就不必在递归中重新计算它们。
1 | class Solution { |
1 | class Solution(object): |
复杂度分析
时间复杂度:O(2^N),对于 N 是奇数的情况,令 N = 2k + 1。然后,\Big| \text{FBT}(N) \Big| = C_k,第 k 个卡特兰数(Catalan Number);以及 \sum\limits_{k < N}{2}} C_k(计算中间结果所涉及的复杂度) 限制在 O(2^N)内。但是,证明超出了本文的范围。
空间复杂度:O(2^N)。
Comments