给你一棵二叉搜索树的 root ,请你 按中序遍历
将其重新排列为一棵递增顺序搜索树,使树中最左边的节点成为树的根节点,并且每个节点没有左子节点,只有一个右子节点。
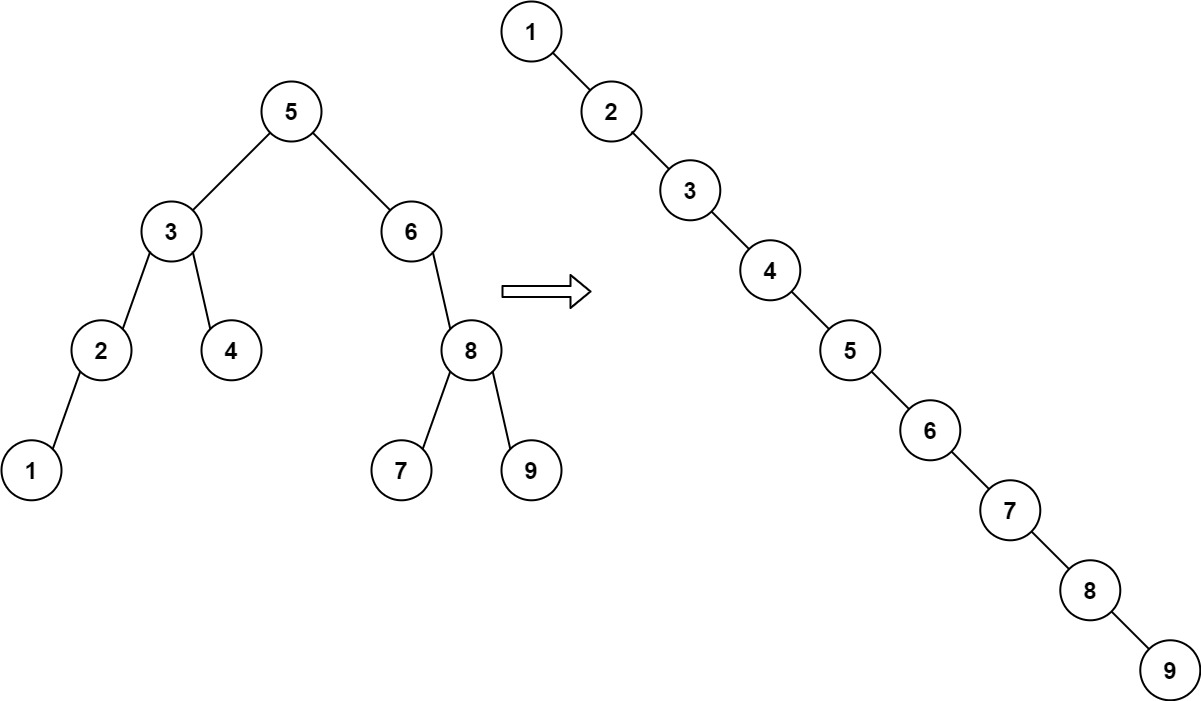
示例 1:

**输入:** root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
**输出:** [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]
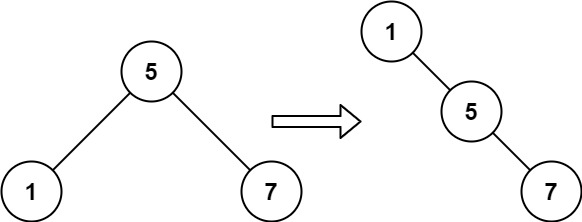
示例 2:

**输入:** root = [5,1,7]
**输出:** [1,null,5,null,7]
提示:
- 树中节点数的取值范围是
[1, 100]
0 <= Node.val <= 1000
方法一:中序遍历之后生成新的树
算法
题目要求我们返回按照中序遍历的结果改造而成的、只有右节点的等价二叉搜索树。我们可以进行如下操作:
代码
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public TreeNode increasingBST(TreeNode root) {
List<Integer> res = new ArrayList<Integer>();
inorder(root, res);
TreeNode dummyNode = new TreeNode(-1);
TreeNode currNode = dummyNode;
for (int value : res) {
currNode.right = new TreeNode(value);
currNode = currNode.right;
}
return dummyNode.right;
}
public void inorder(TreeNode node, List<Integer> res) {
if (node == null) {
return;
}
inorder(node.left, res);
res.add(node.val);
inorder(node.right, res);
}
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| var increasingBST = function(root) {
const res = [];
inorder(root, res);
const dummyNode = new TreeNode(-1);
let currNode = dummyNode;
for (const value of res) {
currNode.right = new TreeNode(value);
currNode = currNode.right;
}
return dummyNode.right;
};
const inorder = (node, res) => {
if (!node) {
return;
}
inorder(node.left, res);
res.push(node.val);
inorder(node.right, res);
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| func increasingBST(root *TreeNode) *TreeNode {
vals := []int{}
var inorder func(*TreeNode)
inorder = func(node *TreeNode) {
if node != nil {
inorder(node.Left)
vals = append(vals, node.Val)
inorder(node.Right)
}
}
inorder(root)
dummyNode := &TreeNode{}
curNode := dummyNode
for _, val := range vals {
curNode.Right = &TreeNode{Val: val}
curNode = curNode.Right
}
return dummyNode.Right
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
public:
void inorder(TreeNode *node, vector<int> &res) {
if (node == nullptr) {
return;
}
inorder(node->left, res);
res.push_back(node->val);
inorder(node->right, res);
}
TreeNode *increasingBST(TreeNode *root) {
vector<int> res;
inorder(root, res);
TreeNode *dummyNode = new TreeNode(-1);
TreeNode *currNode = dummyNode;
for (int value : res) {
currNode->right = new TreeNode(value);
currNode = currNode->right;
}
return dummyNode->right;
}
};
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| struct TreeNode* createTreeNode(int val) {
struct TreeNode* ret = malloc(sizeof(struct TreeNode));
ret->val = val, ret->left = ret->right = NULL;
return ret;
}
void inorder(struct TreeNode* node, int* res, int* resSize) {
if (node == NULL) {
return;
}
inorder(node->left, res, resSize);
res[(*resSize)++] = node->val;
inorder(node->right, res, resSize);
}
struct TreeNode* increasingBST(struct TreeNode* root) {
int res[100], resSize = 0;
inorder(root, res, &resSize);
struct TreeNode* dummyNode = createTreeNode(-1);
struct TreeNode* currNode = dummyNode;
for (int i = 0; i < resSize; i++) {
currNode->right = createTreeNode(res[i]);
currNode = currNode->right;
}
return dummyNode->right;
}
|
复杂度分析
方法二:在中序遍历的过程中改变节点指向
算法
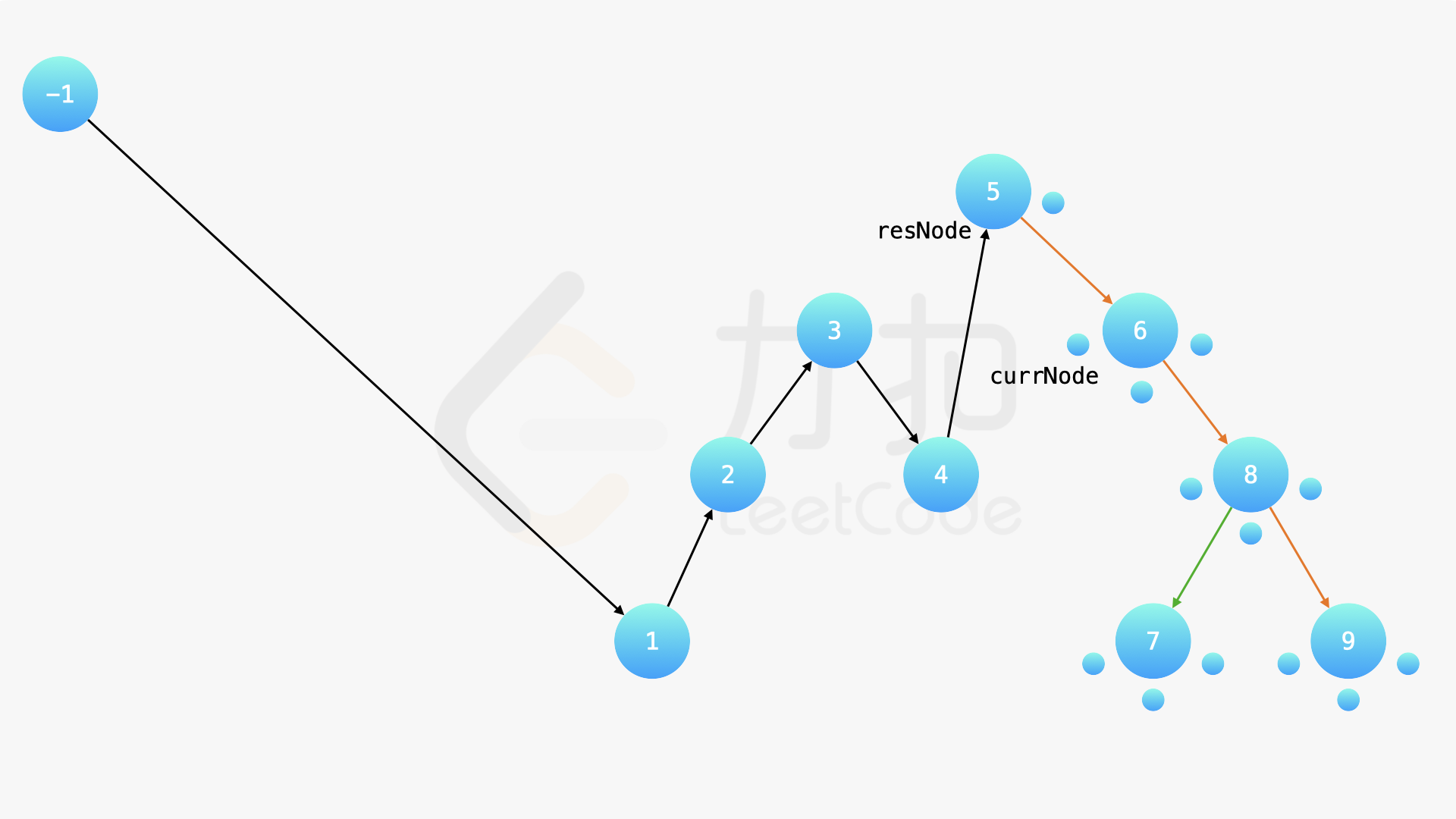
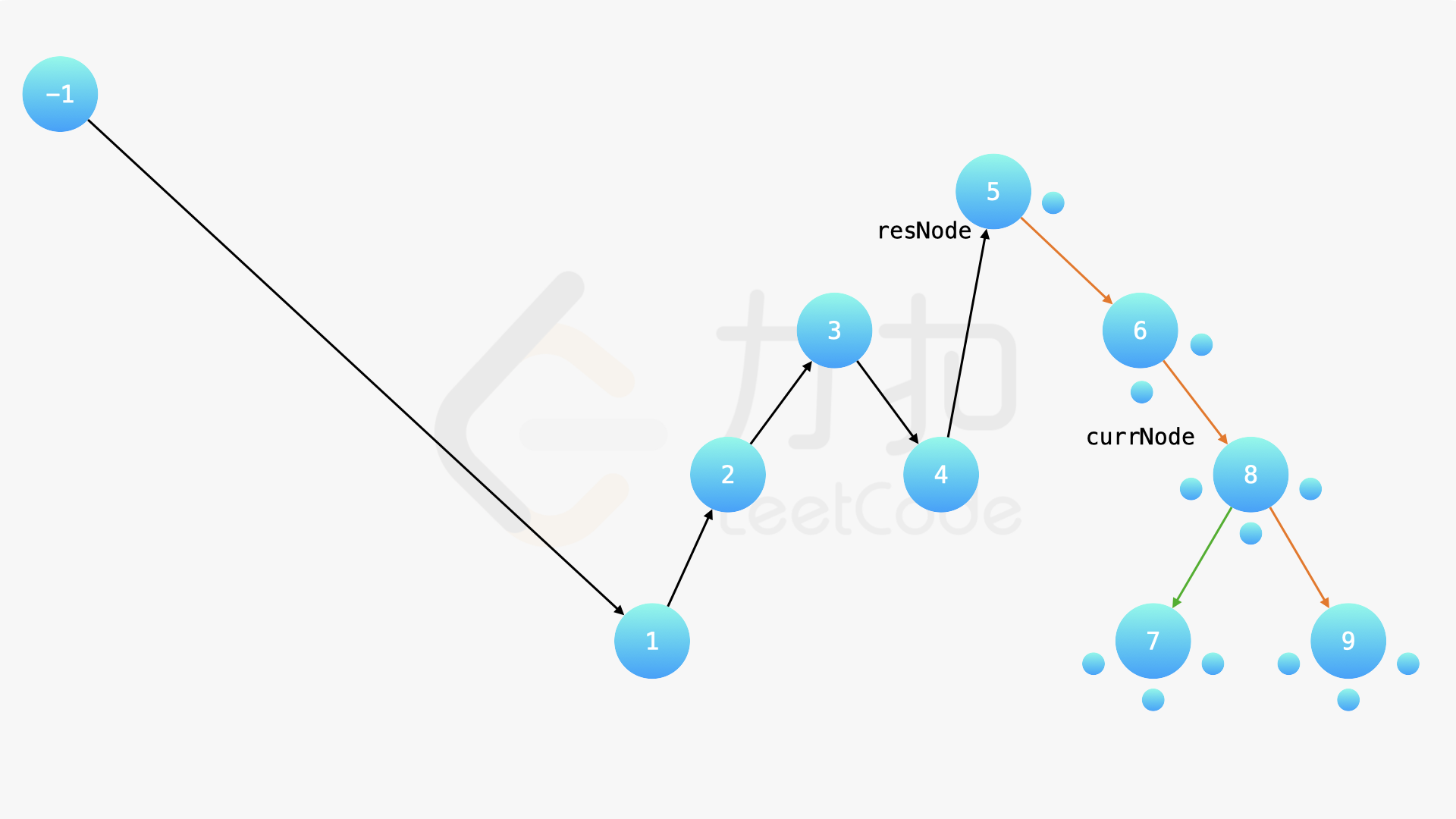
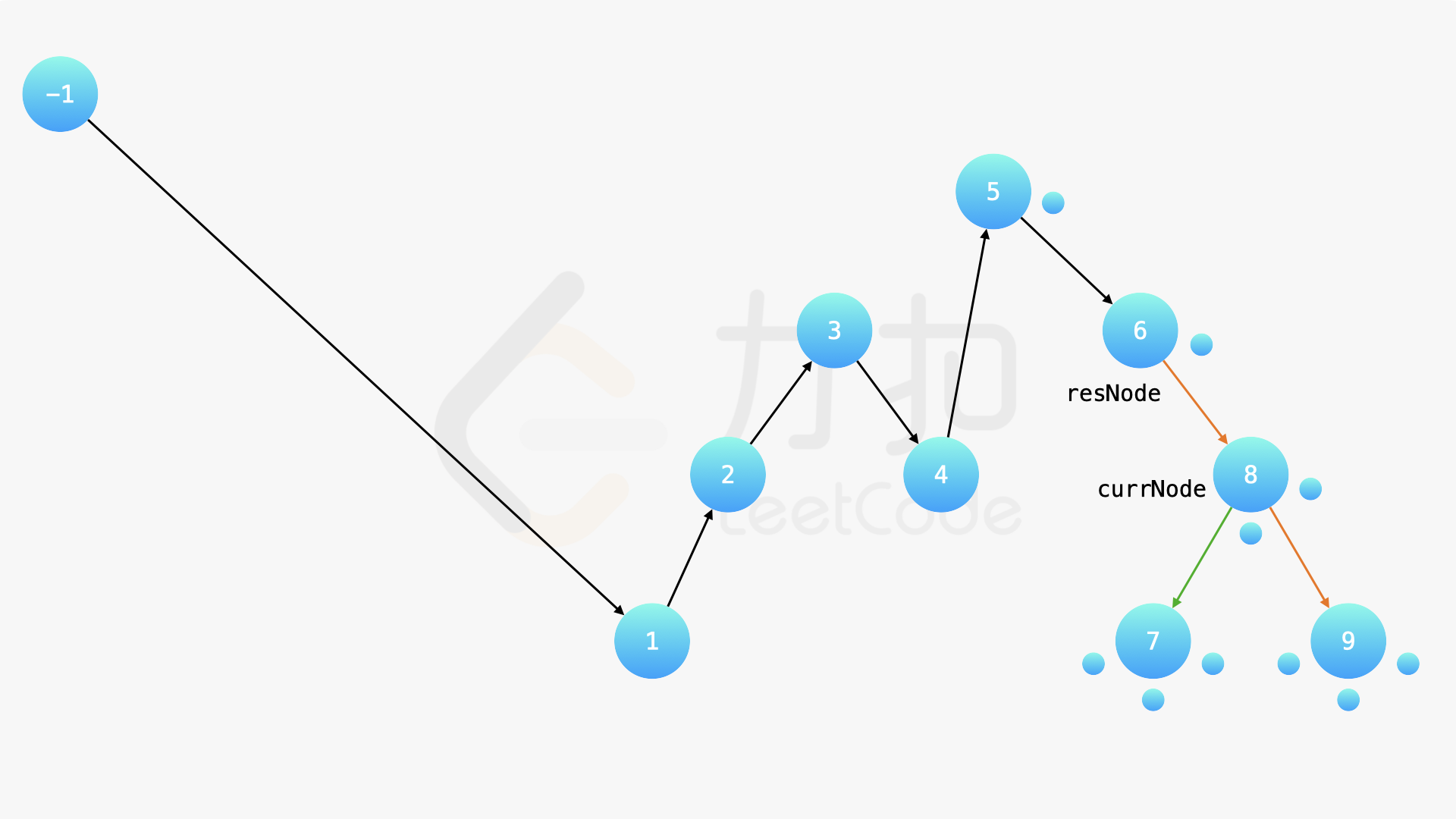
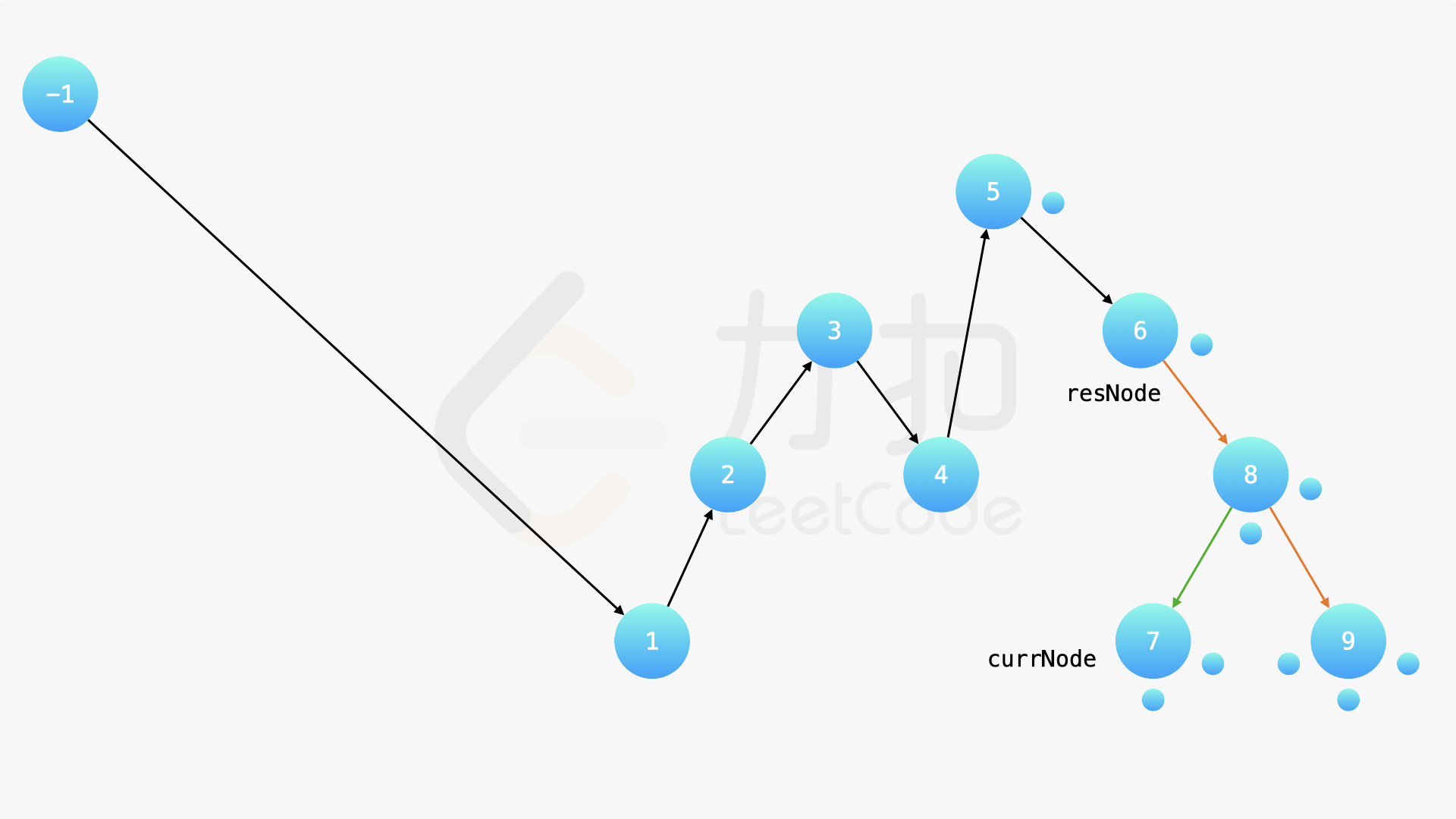
方法一需要遍历一次二叉搜索树以后,然后再创建新的等价的二叉搜索树。事实上,还可以遍历一次输入二叉搜索树,在遍历的过程中改变节点指向以满足题目的要求。
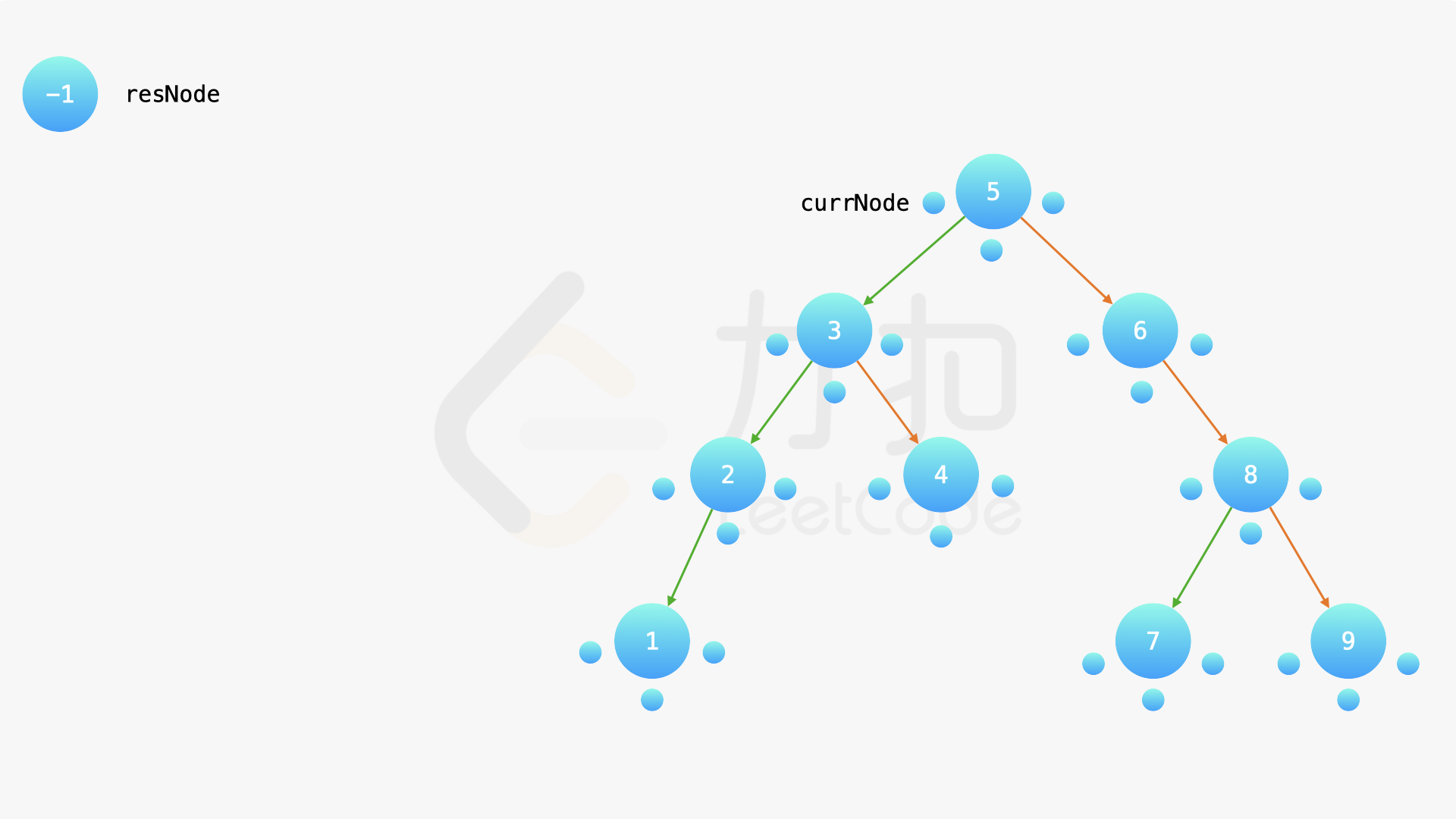
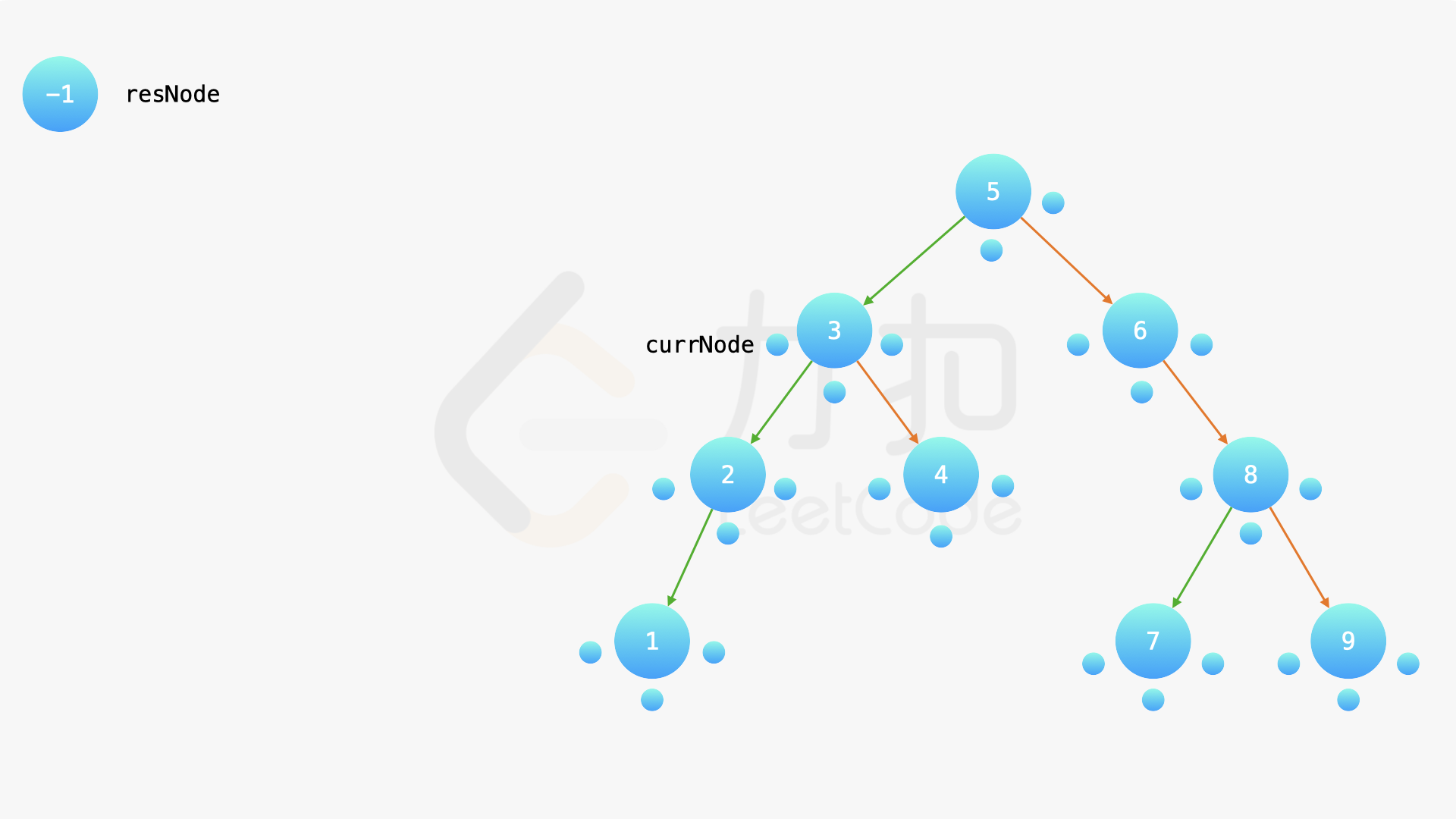
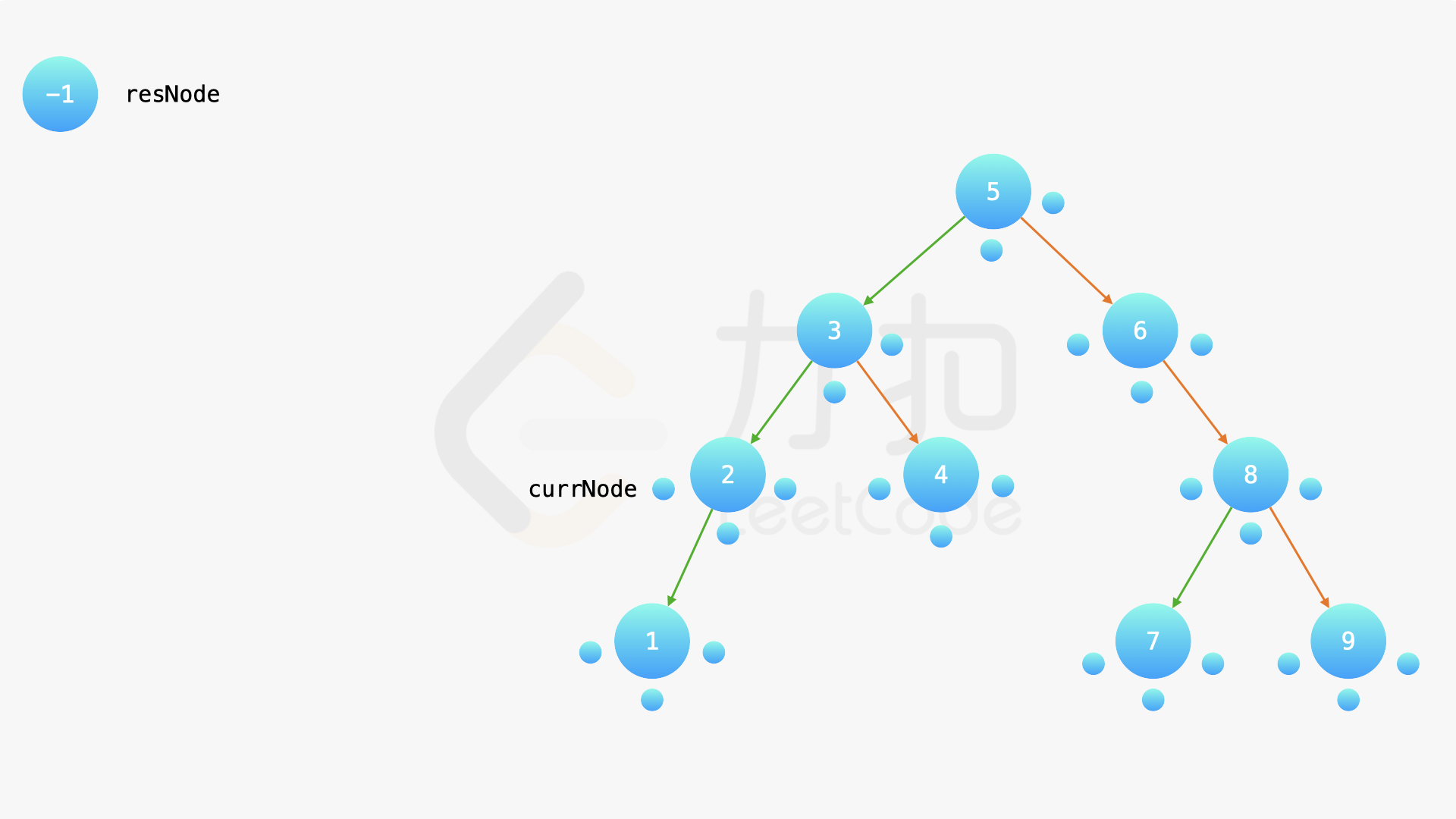
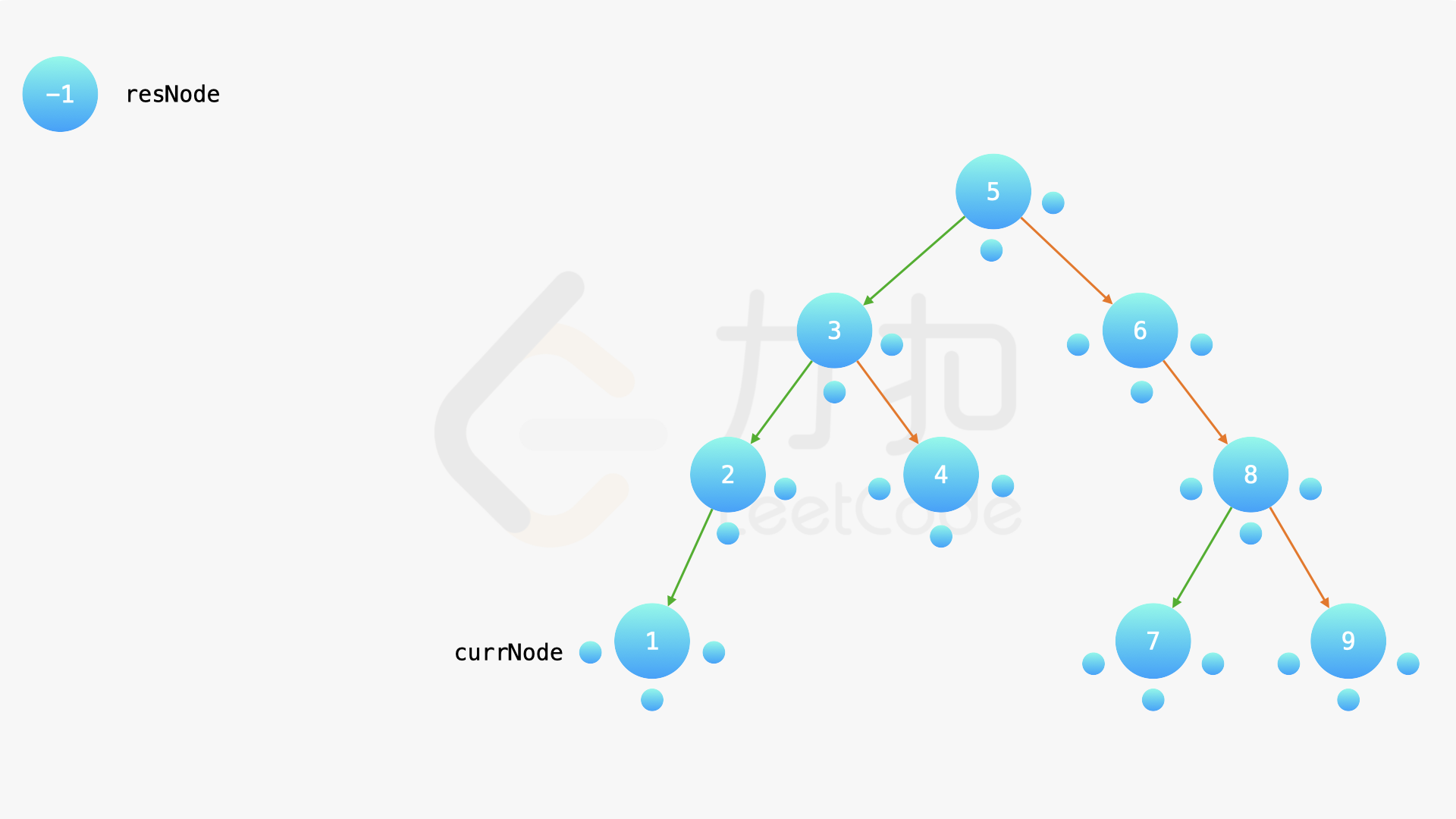
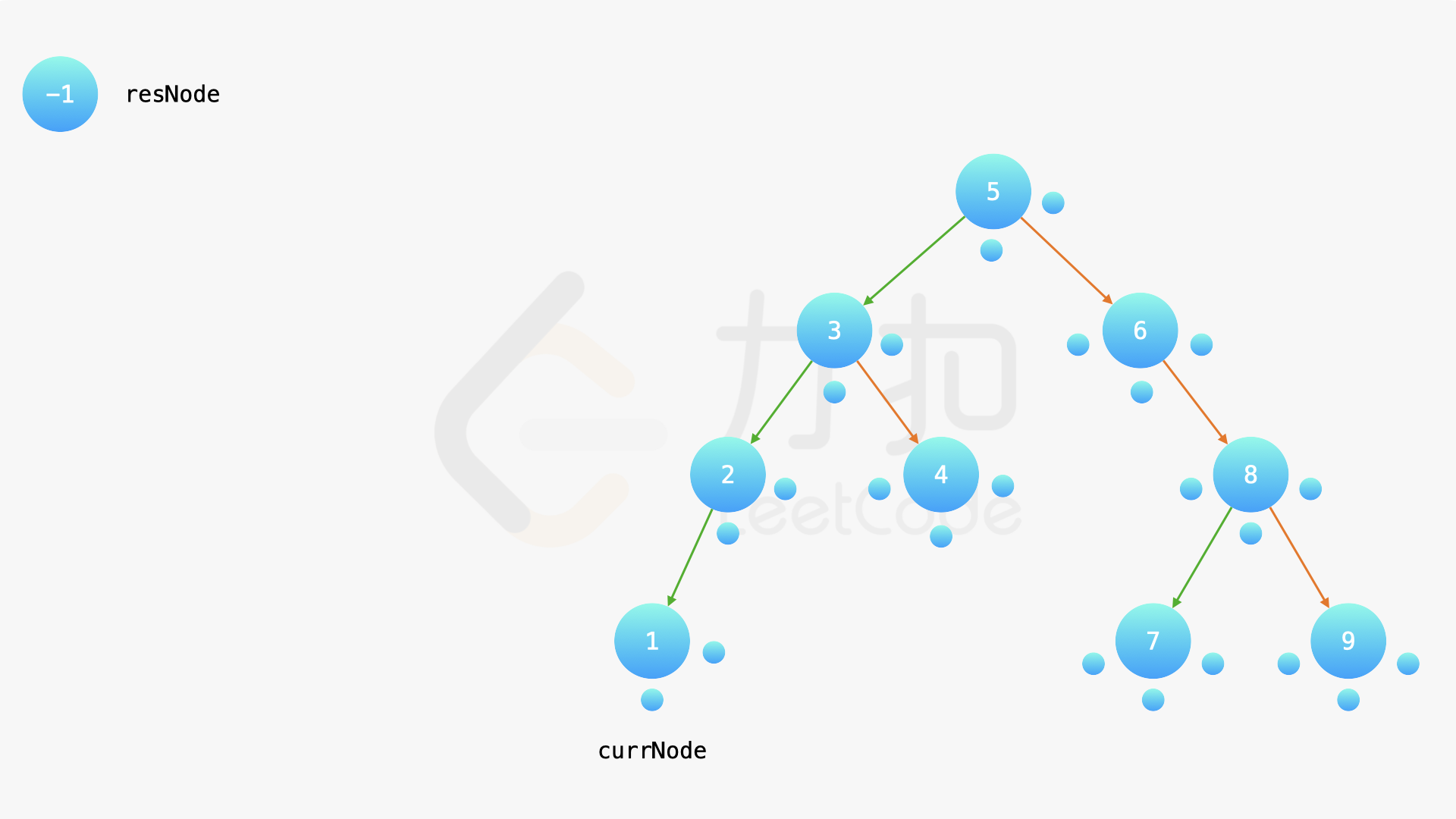
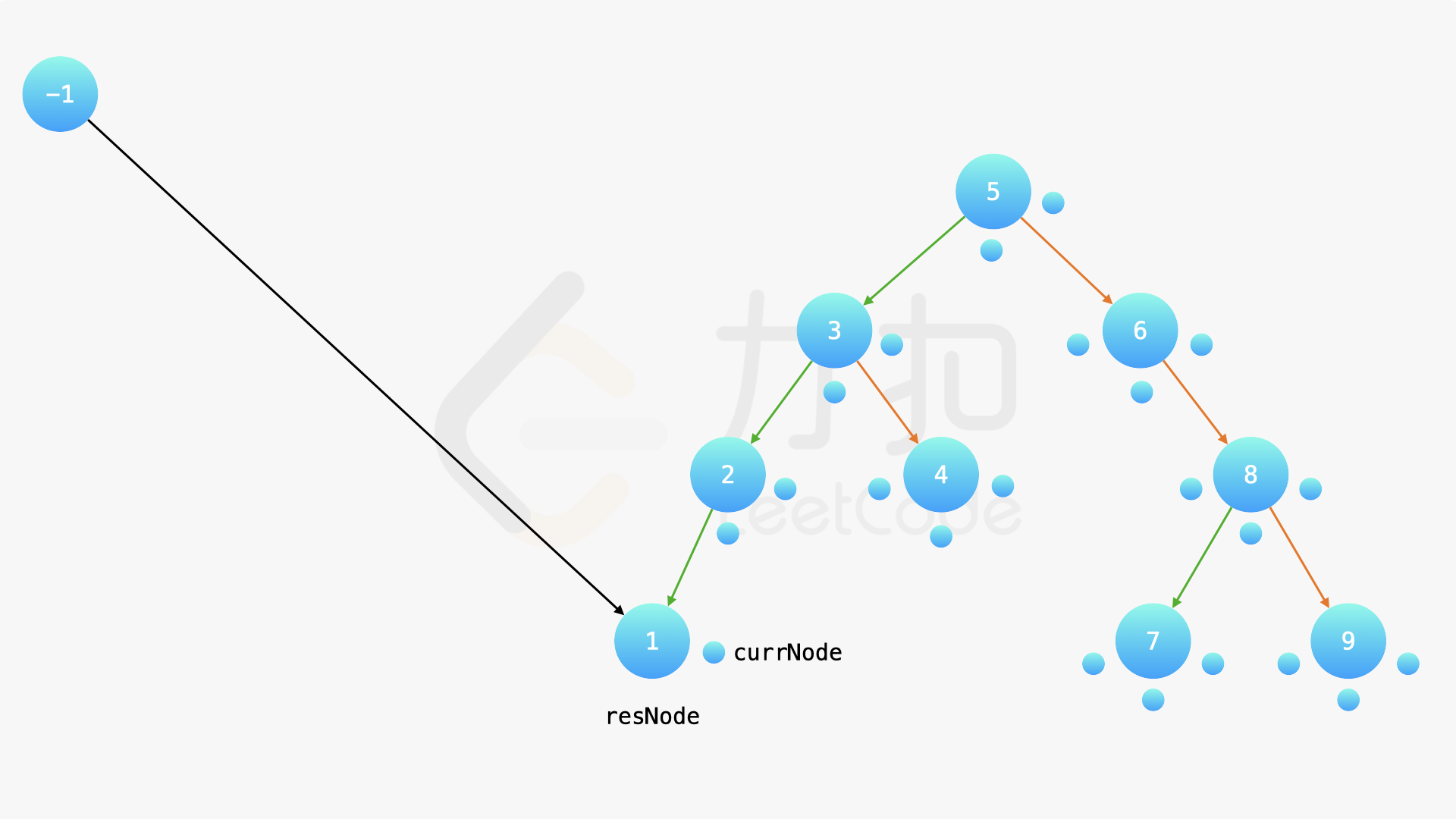
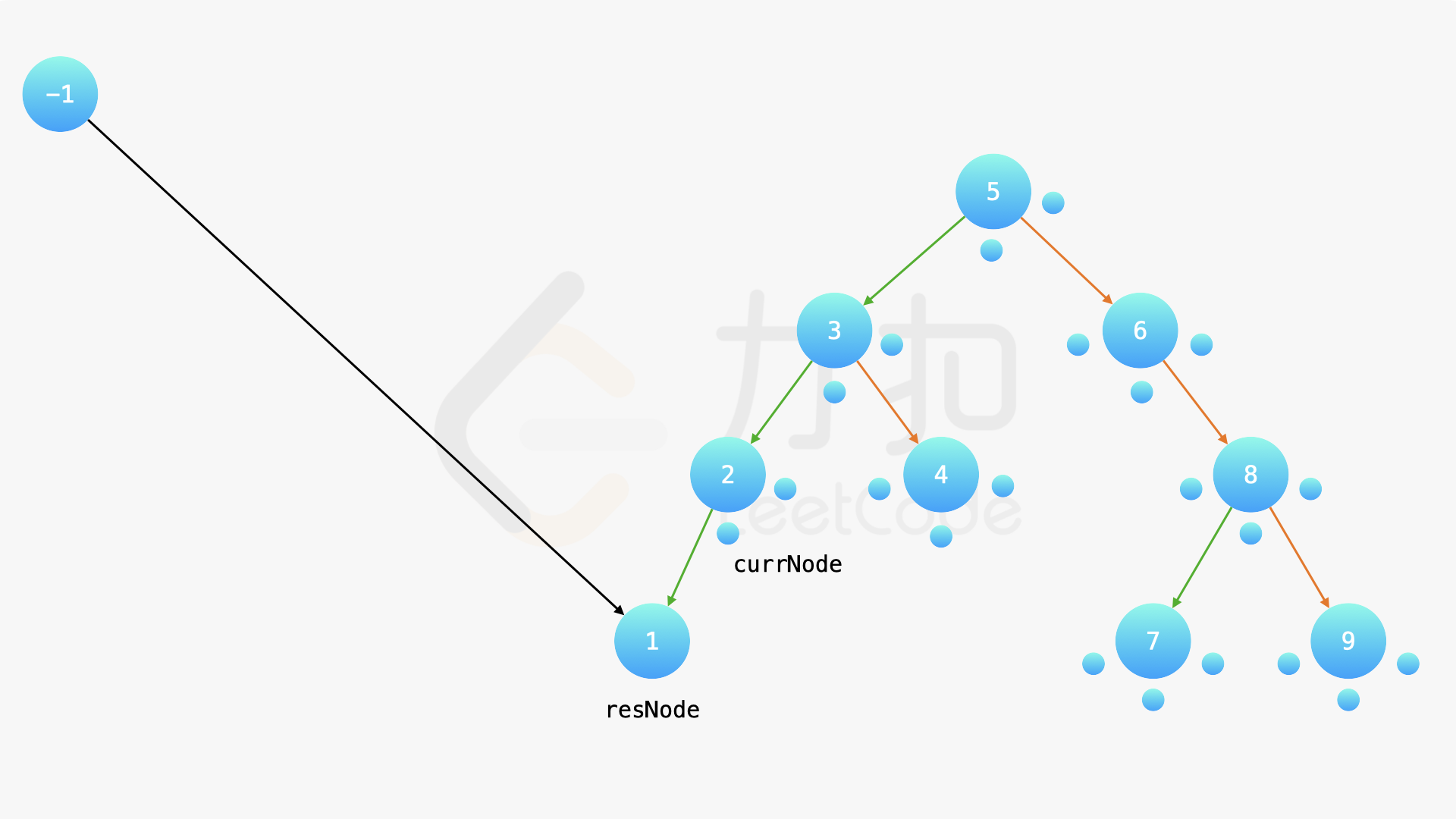
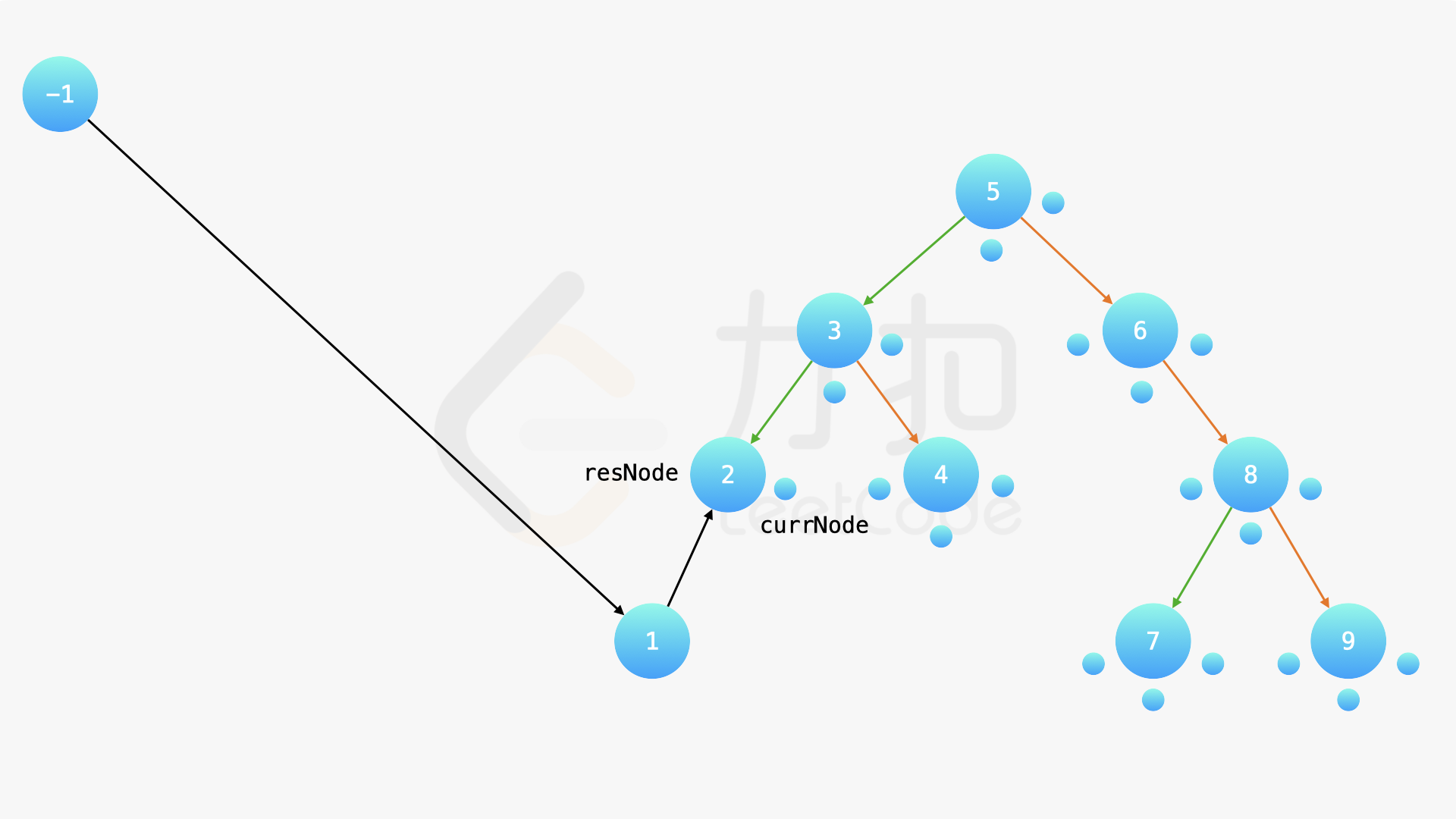
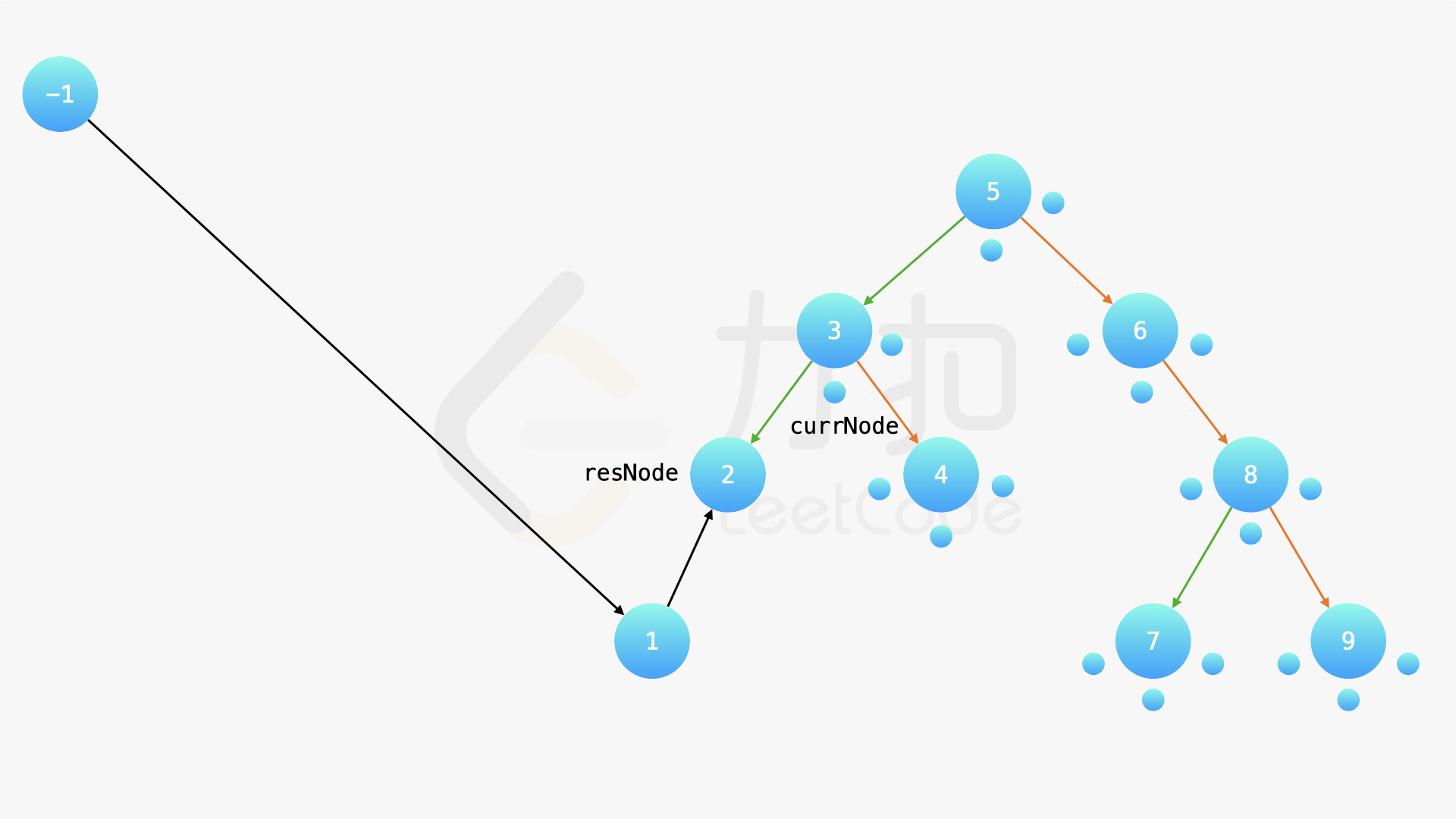
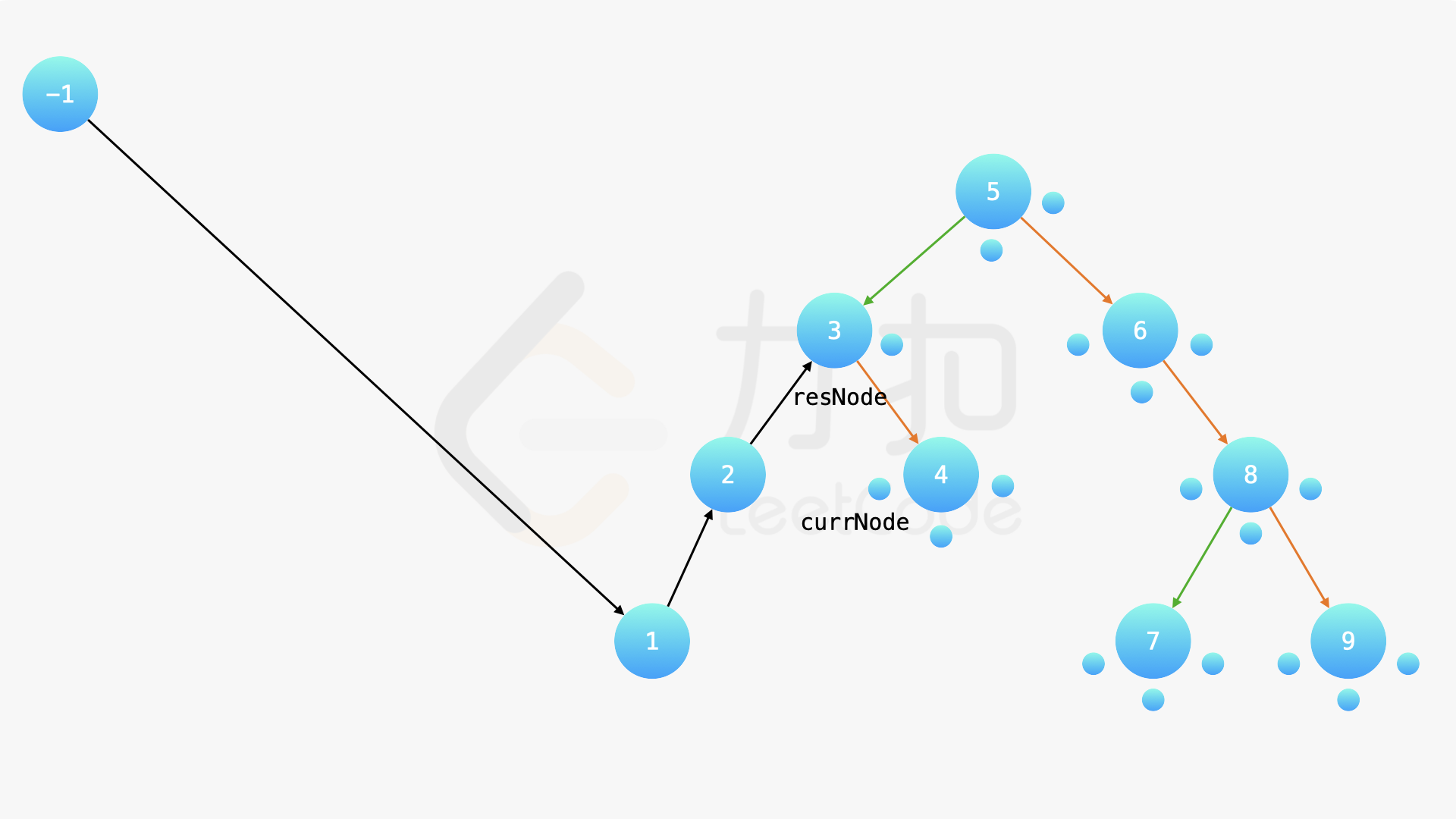
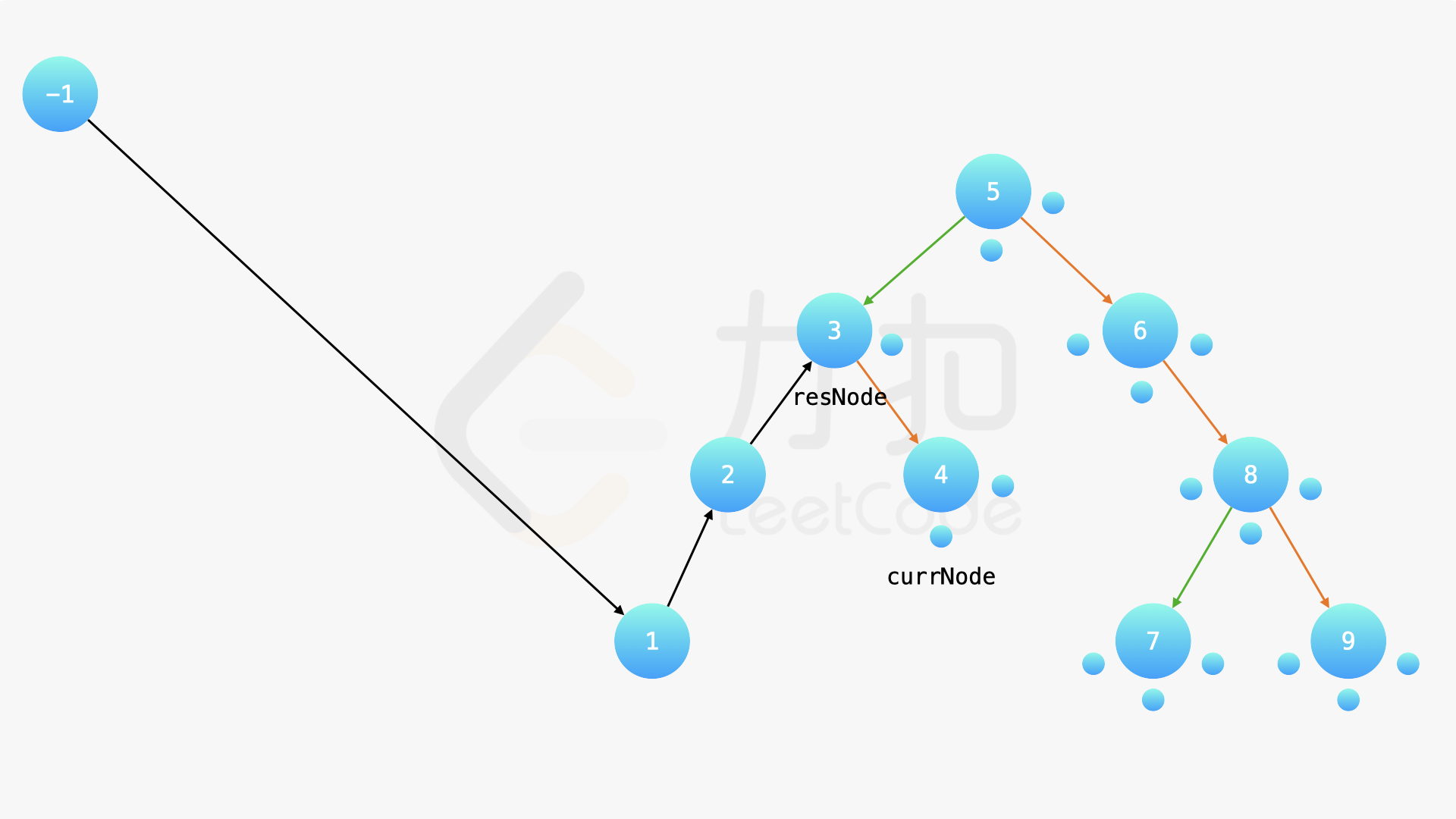
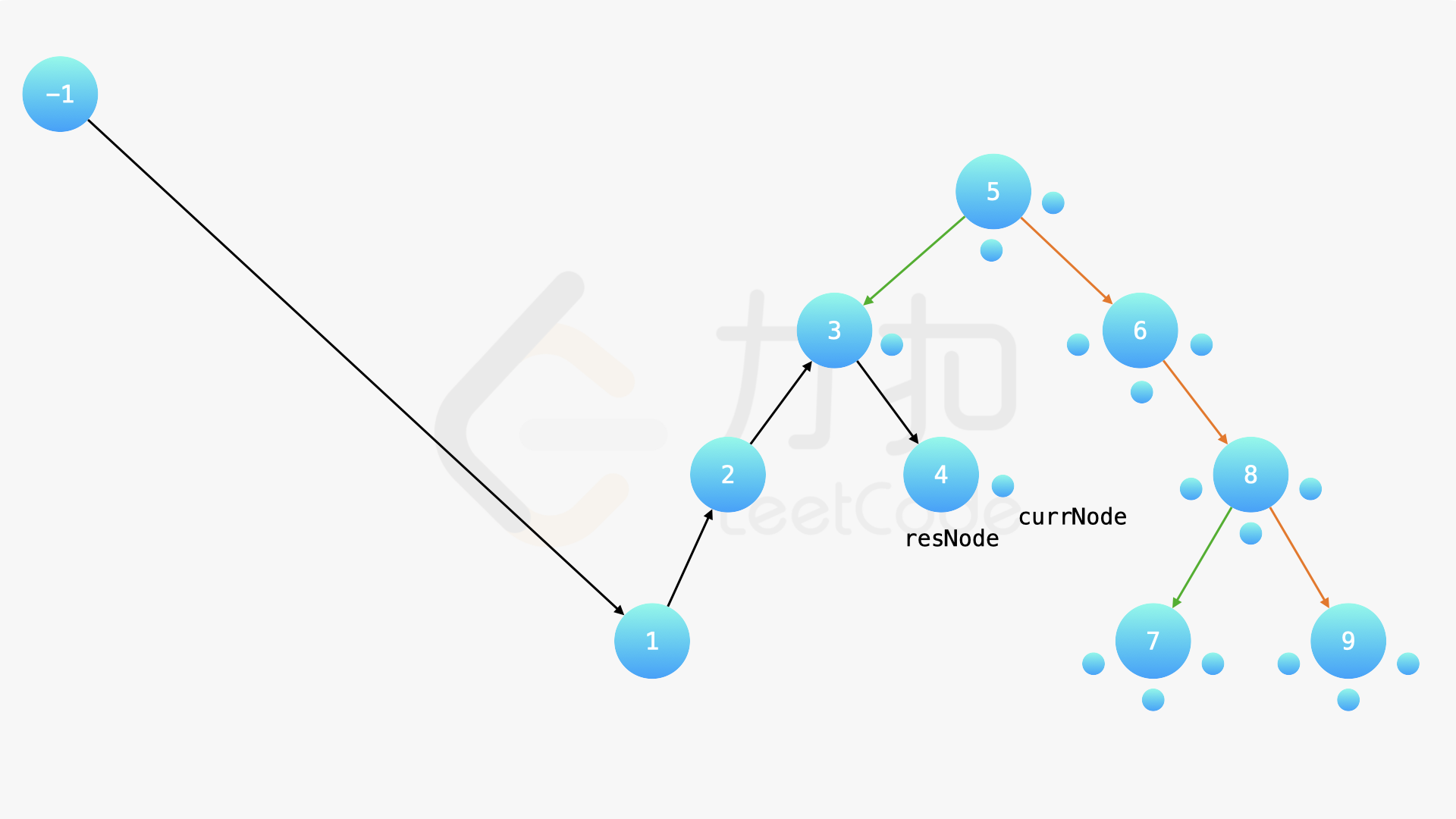
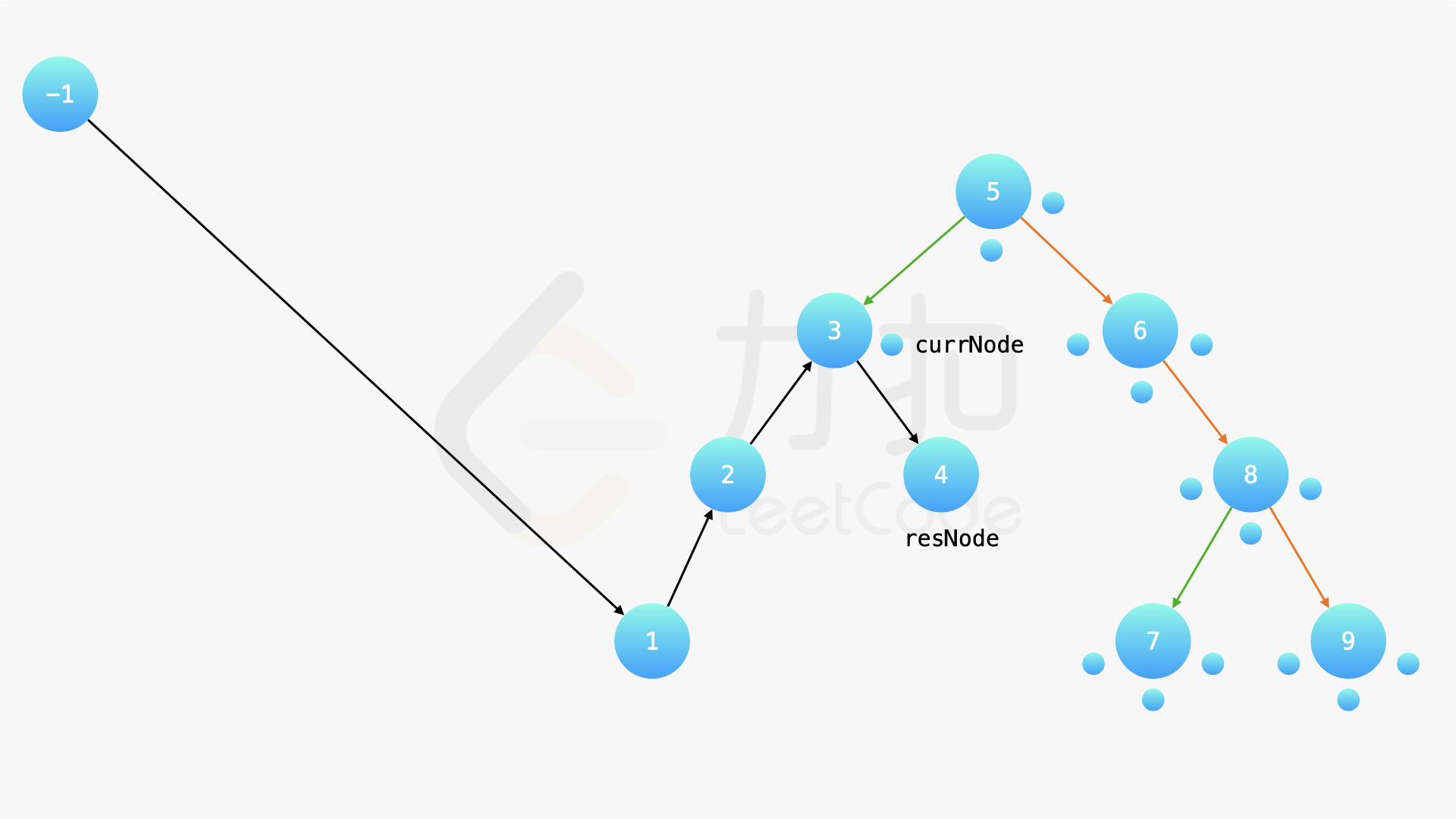
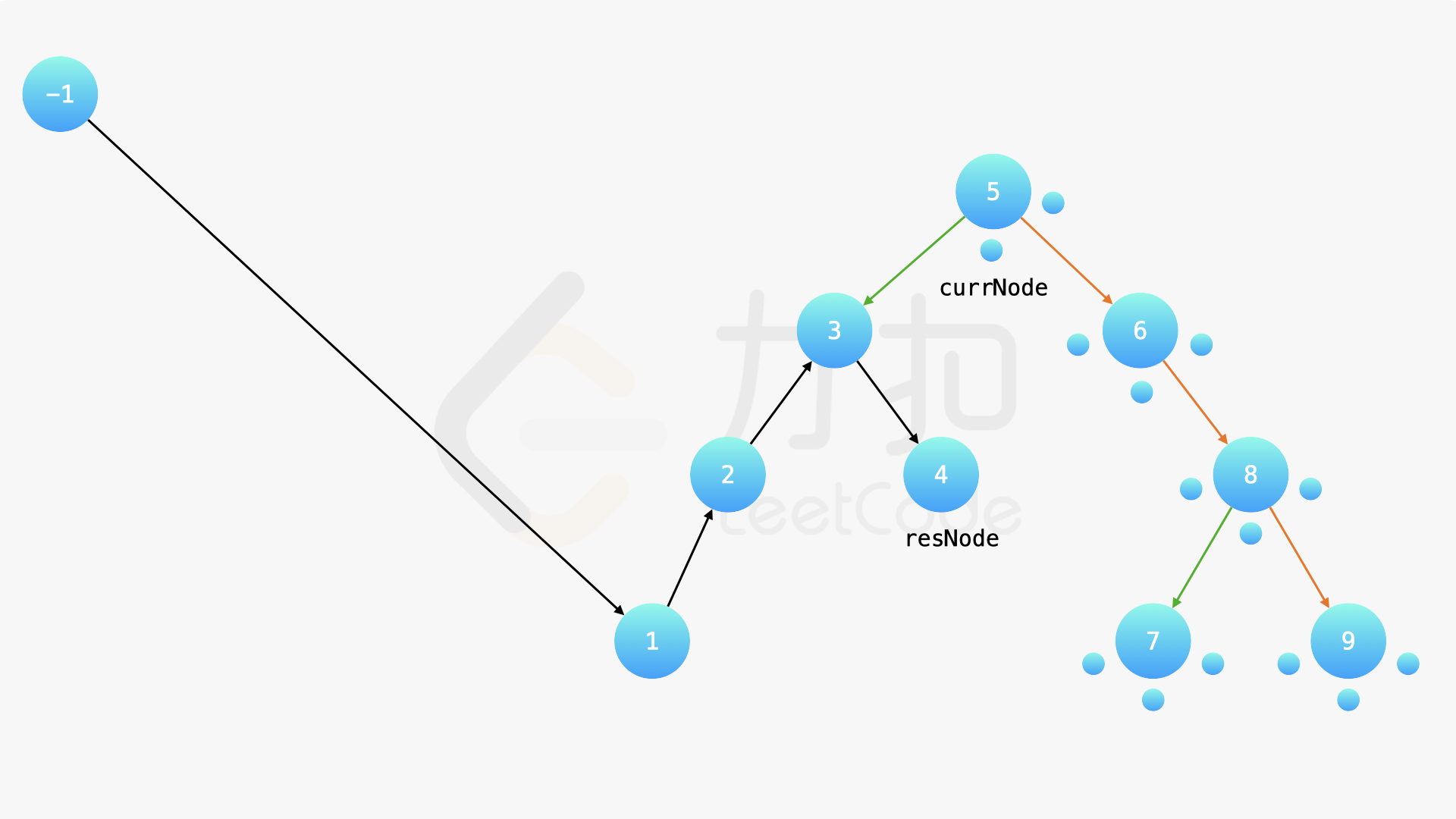
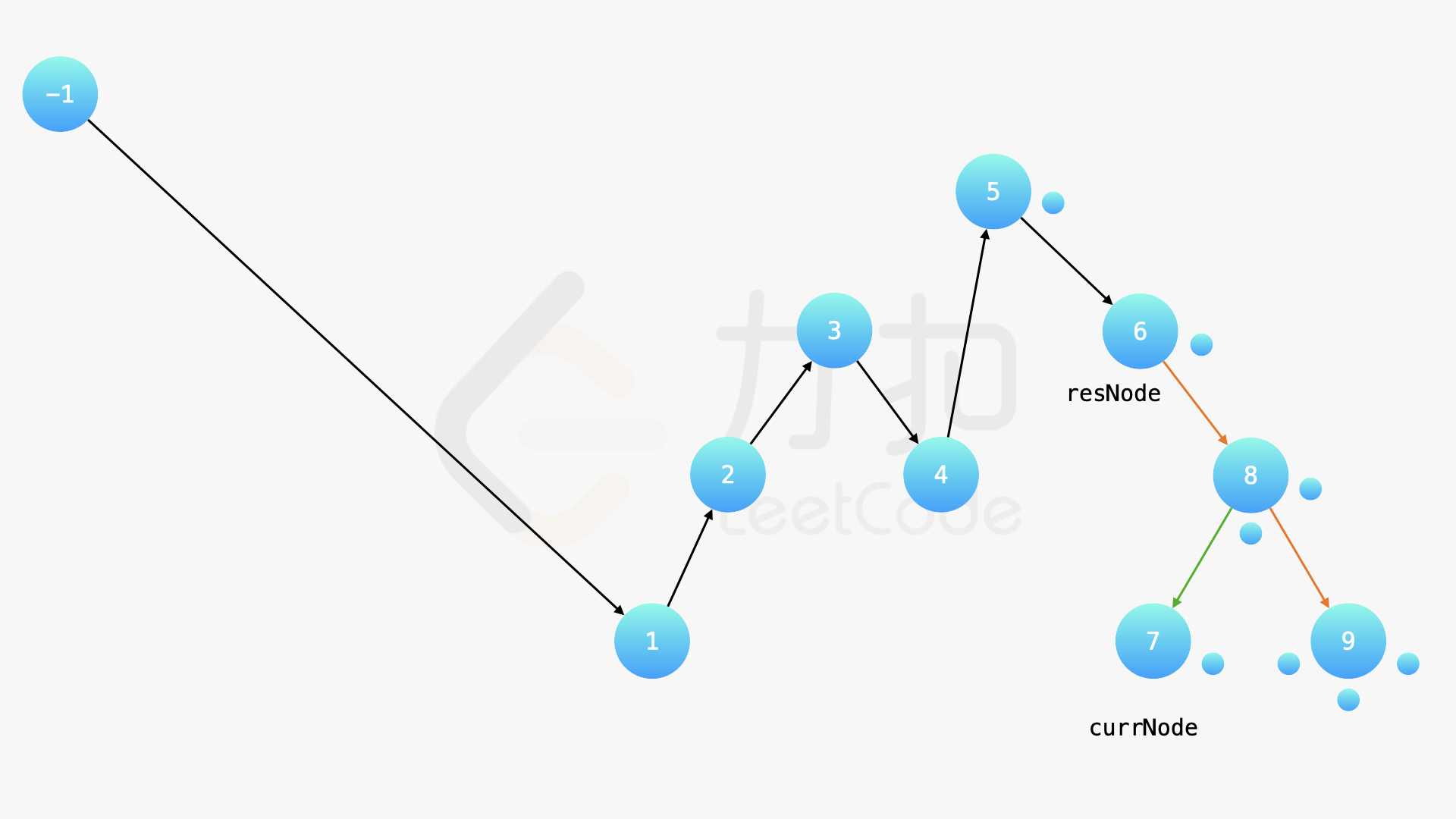
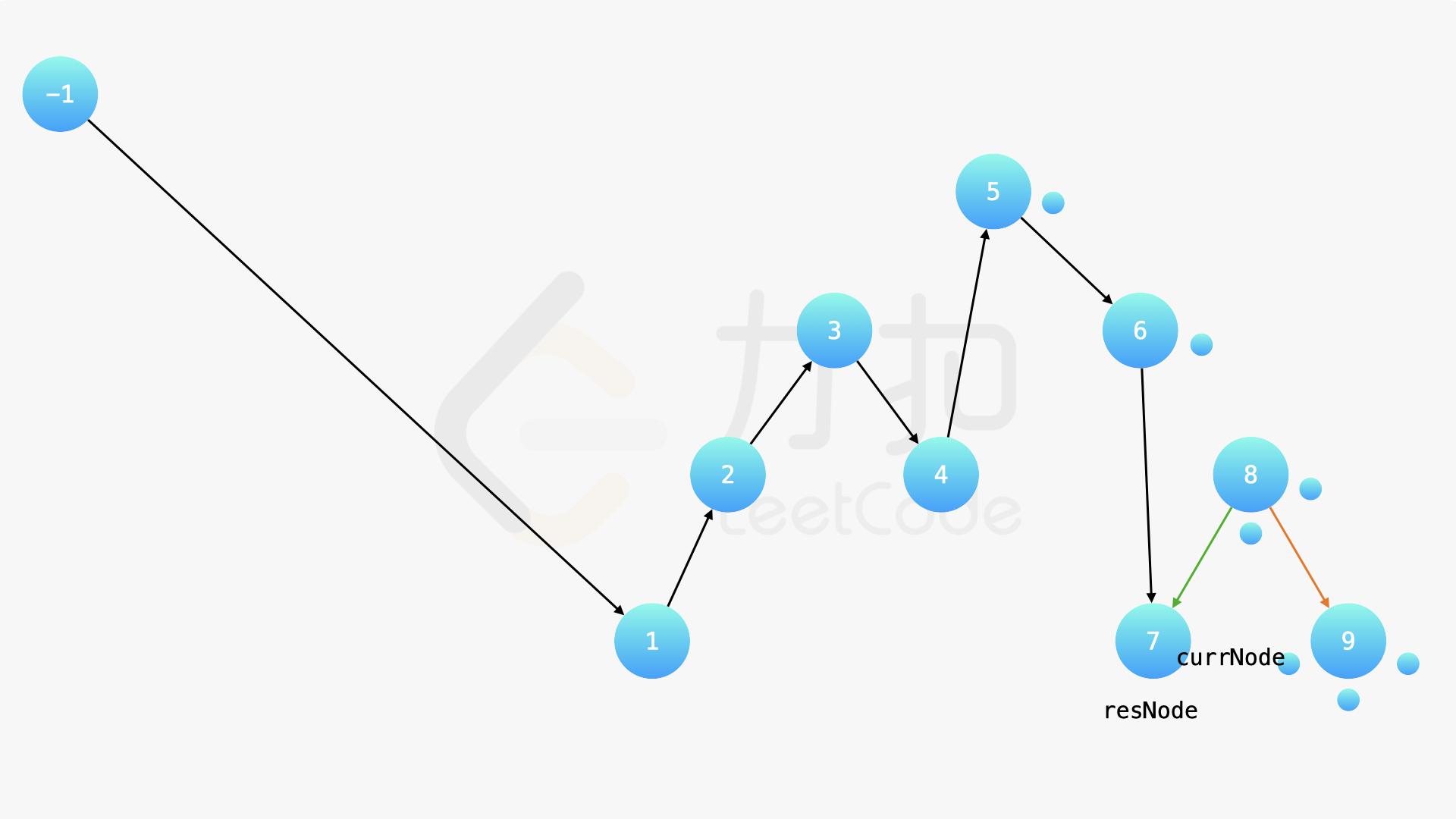
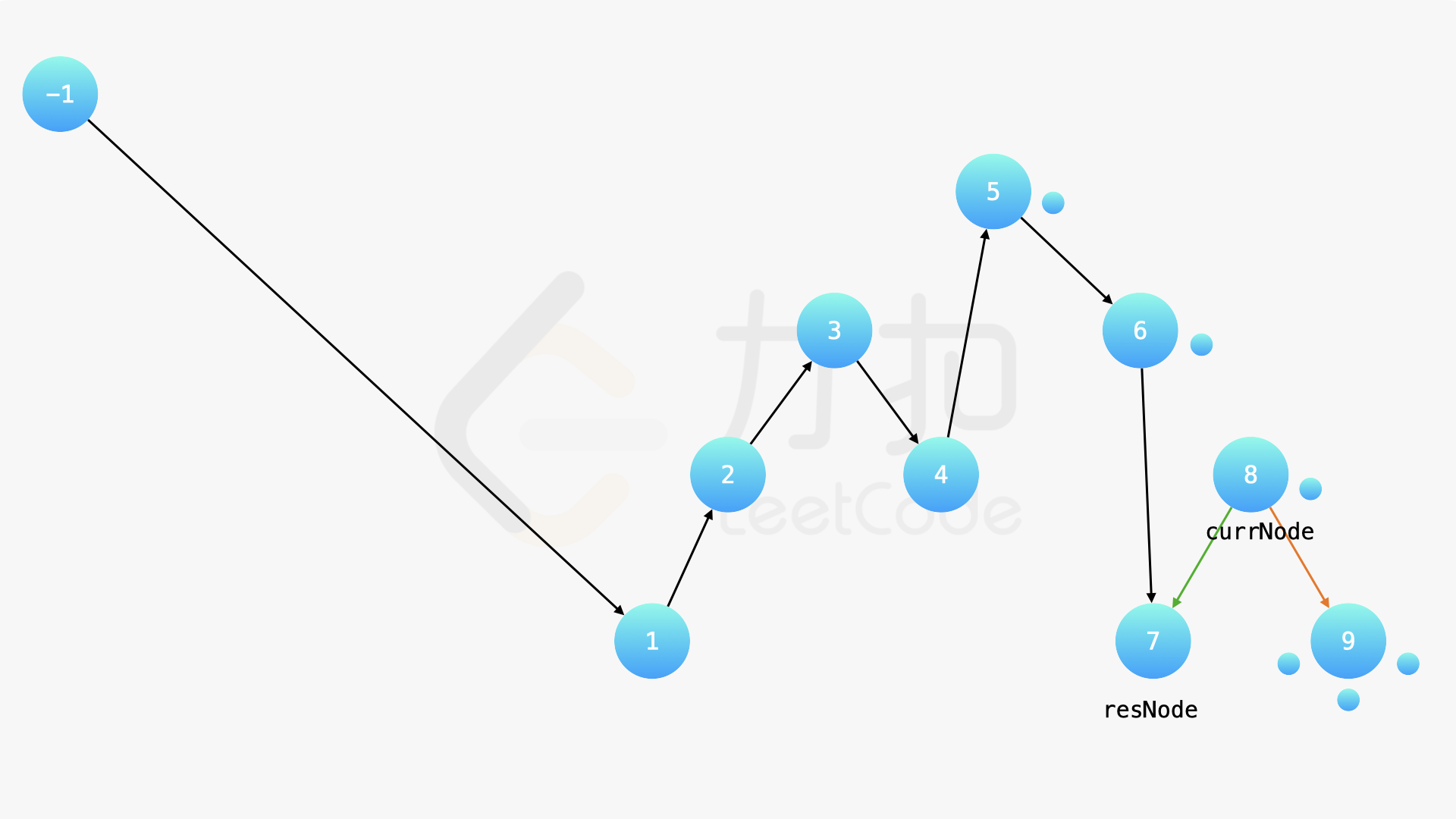
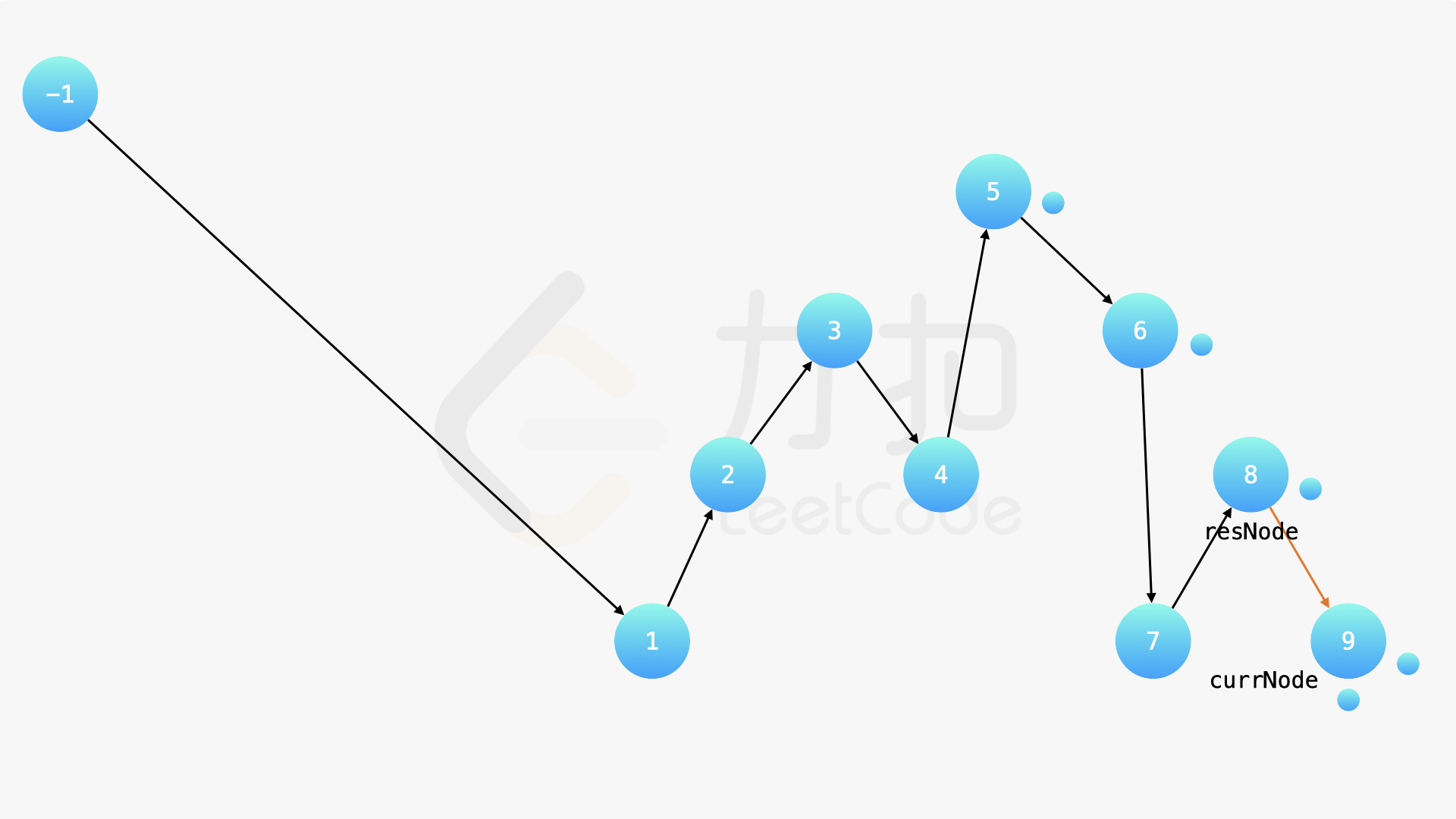
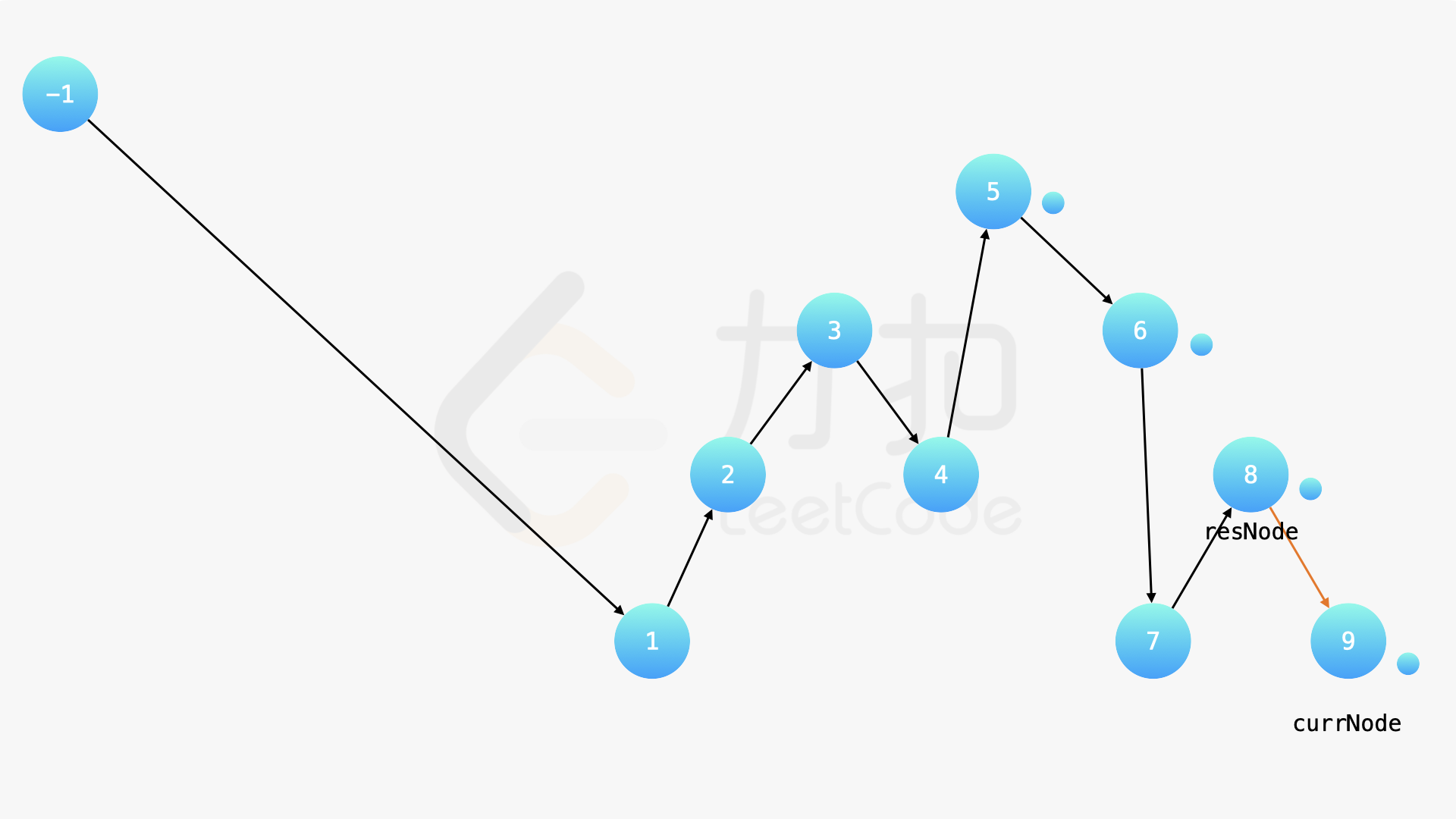
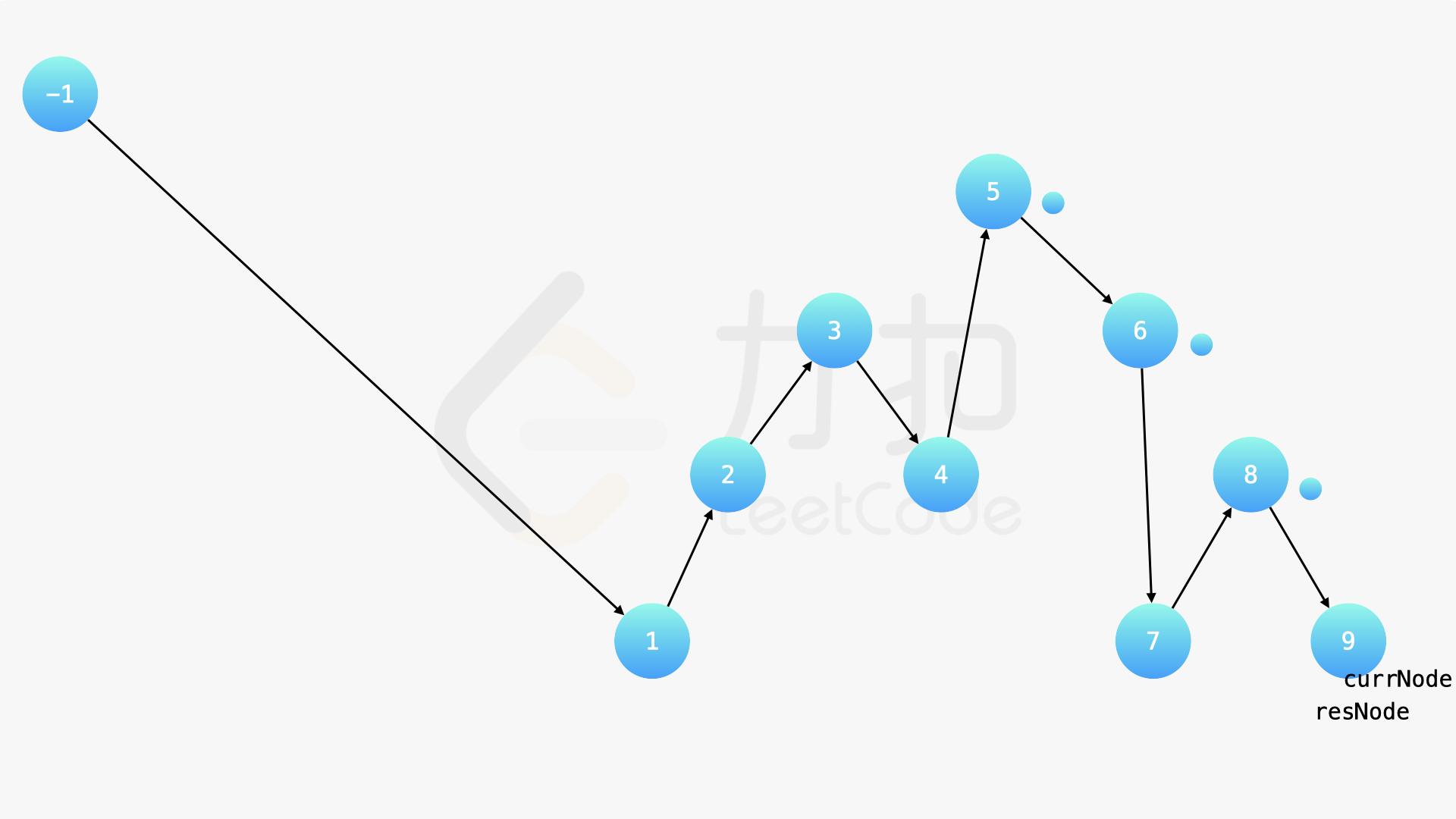
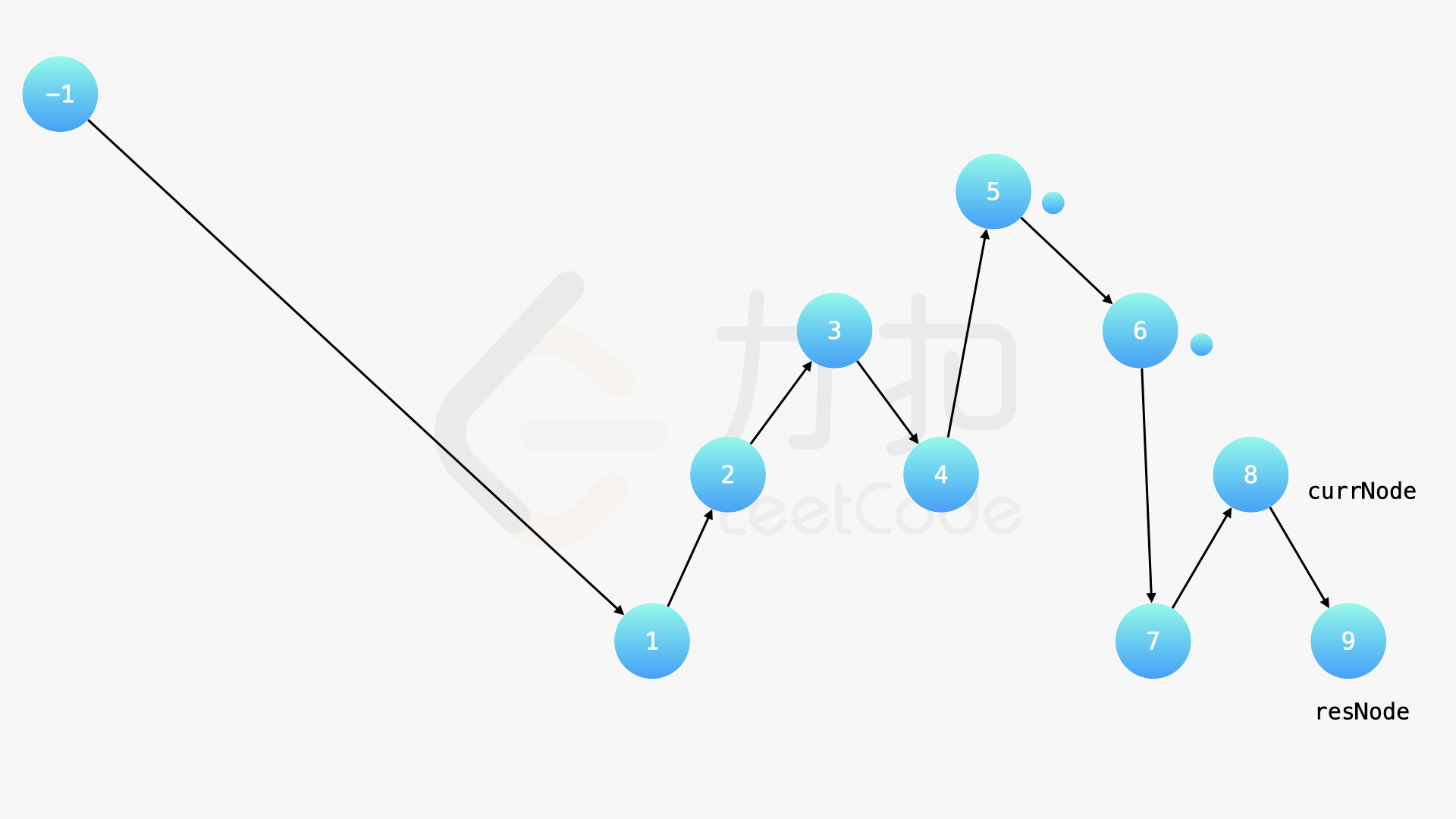
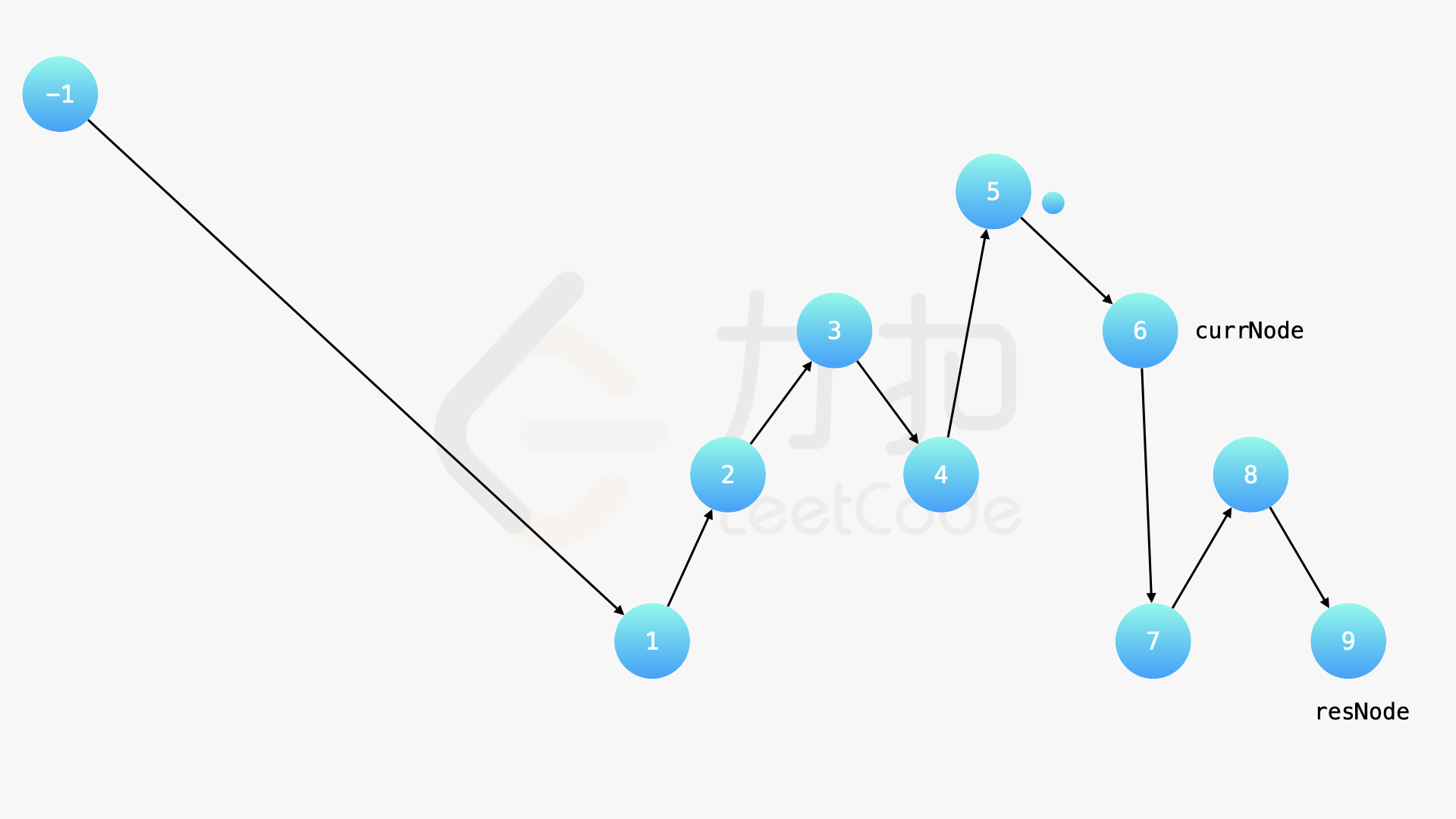
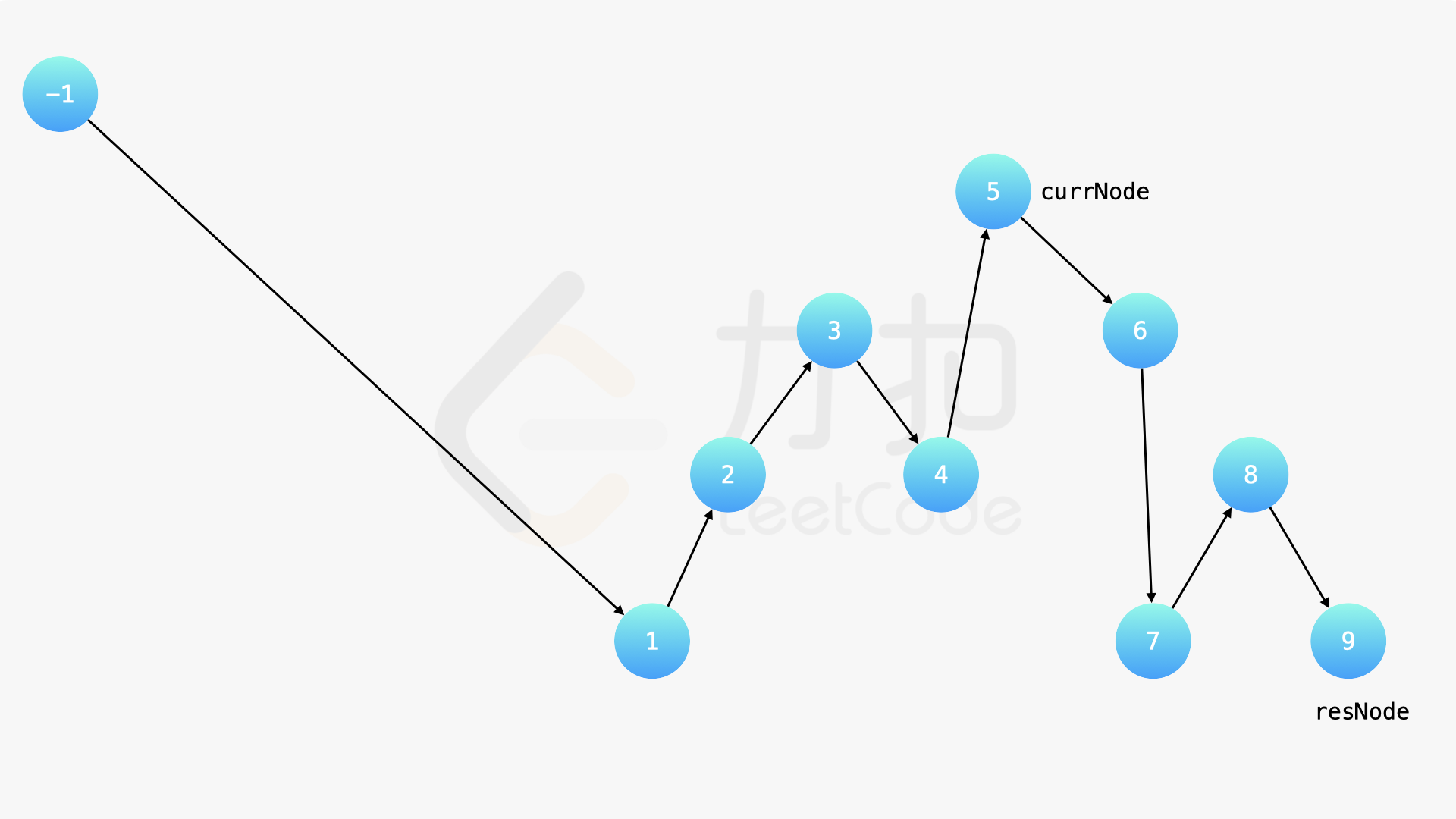
在中序遍历的时候,修改节点指向就可以实现。具体地,当我们遍历到一个节点时,把它的左孩子设为空,并将其本身作为上一个遍历到的节点的右孩子。这里需要有一些想象能力。递归遍历的过程中,由于递归函数的调用栈保存了节点的引用,因此上述操作可以实现。下面的幻灯片展示了这样的过程。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码
[sol2-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| class Solution {
private TreeNode resNode;
public TreeNode increasingBST(TreeNode root) {
TreeNode dummyNode = new TreeNode(-1);
resNode = dummyNode;
inorder(root);
return dummyNode.right;
}
public void inorder(TreeNode node) {
if (node == null) {
return;
}
inorder(node.left);
resNode.right = node;
node.left = null;
resNode = node;
inorder(node.right);
}
}
|
[sol2-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| var increasingBST = function(root) {
const dummyNode = new TreeNode(-1);
let resNode = dummyNode;
const inorder = (node) => {
if (!node) {
return;
}
inorder(node.left);
resNode.right = node;
node.left = null;
resNode = node;
inorder(node.right);
}
inorder(root);
return dummyNode.right;
};
|
[sol2-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| func increasingBST(root *TreeNode) *TreeNode {
dummyNode := &TreeNode{}
resNode := dummyNode
var inorder func(*TreeNode)
inorder = func(node *TreeNode) {
if node == nil {
return
}
inorder(node.Left)
resNode.Right = node
node.Left = nil
resNode = node
inorder(node.Right)
}
inorder(root)
return dummyNode.Right
}
|
[sol2-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| class Solution {
private:
TreeNode *resNode;
public:
void inorder(TreeNode *node) {
if (node == nullptr) {
return;
}
inorder(node->left);
resNode->right = node;
node->left = nullptr;
resNode = node;
inorder(node->right);
}
TreeNode *increasingBST(TreeNode *root) {
TreeNode *dummyNode = new TreeNode(-1);
resNode = dummyNode;
inorder(root);
return dummyNode->right;
}
};
|
[sol2-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| struct TreeNode* createTreeNode(int val) {
struct TreeNode* ret = malloc(sizeof(struct TreeNode));
ret->val = val, ret->left = ret->right = NULL;
return ret;
}
struct TreeNode* resNode;
void inorder(struct TreeNode* node) {
if (node == NULL) {
return;
}
inorder(node->left);
resNode->right = node;
node->left = NULL;
resNode = node;
inorder(node->right);
}
struct TreeNode* increasingBST(struct TreeNode* root) {
struct TreeNode* dummyNode = createTreeNode(-1);
resNode = dummyNode;
inorder(root);
return dummyNode->right;
}
|
复杂度分析
4 月 22 日至 4 月 28 日,进入「学习 」,完成页面右上角的「让时间更有价值」限时阅读任务,可获得「2021 读书日纪念勋章」。更多活动详情戳上方标题了解更多👆
今日学习任务:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>