0913-猫和老鼠
两位玩家分别扮演猫和老鼠,在一张 无向 图上进行游戏,两人轮流行动。
图的形式是:graph[a] 是一个列表,由满足 ab 是图中的一条边的所有节点 b 组成。
老鼠从节点 1 开始,第一个出发;猫从节点 2 开始,第二个出发。在节点 0 处有一个洞。
在每个玩家的行动中,他们 必须 沿着图中与所在当前位置连通的一条边移动。例如,如果老鼠在节点 1 ,那么它必须移动到 graph[1]
中的任一节点。
此外,猫无法移动到洞中(节点 0)。
然后,游戏在出现以下三种情形之一时结束:
- 如果猫和老鼠出现在同一个节点,猫获胜。
- 如果老鼠到达洞中,老鼠获胜。
- 如果某一位置重复出现(即,玩家的位置和移动顺序都与上一次行动相同),游戏平局。
给你一张图 graph ,并假设两位玩家都都以最佳状态参与游戏:
- 如果老鼠获胜,则返回
1; - 如果猫获胜,则返回
2; - 如果平局,则返回
0。
示例 1:
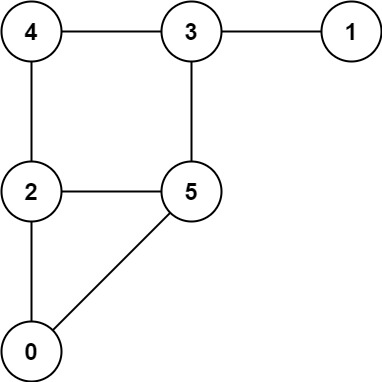
**输入:** graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]
**输出:** 0
示例 2:
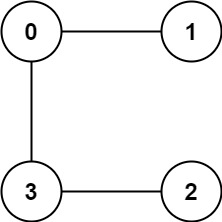
**输入:** graph = [[1,3],[0],[3],[0,2]]
**输出:** 1
提示:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]互不相同- 猫和老鼠在游戏中总是可以移动
前言
博弈知识介绍
这道题是博弈问题,猫和老鼠都按照最优策略参与游戏。
在阐述具体解法之前,首先介绍博弈问题中的三个概念:必胜状态、必败状态与必和状态。
对于特定状态,如果游戏已经结束,则根据结束时的状态决定必胜状态、必败状态与必和状态。
如果分出胜负,则该特定状态对于获胜方为必胜状态,对于落败方为必败状态。
如果是平局,则该特定状态对于双方都为必和状态。
从特定状态开始,如果存在一种操作将状态变成必败状态,则当前玩家可以选择该操作,将必败状态留给对方玩家,因此该特定状态对于当前玩家为必胜状态。
从特定状态开始,如果所有操作都会将状态变成必胜状态,则无论当前玩家选择哪种操作,都会将必胜状态留给对方玩家,因此该特定状态对于当前玩家为必败状态。
从特定状态开始,如果任何操作都不能将状态变成必败状态,但是存在一种操作将状态变成必和状态,则当前玩家可以选择该操作,将必和状态留给对方玩家,因此该特定状态对于双方玩家都为必和状态。
对于每个玩家,最优策略如下:
争取将必胜状态留给自己,将必败状态留给对方玩家。
在自己无法到达必胜状态的情况下,争取将必和状态留给自己。
自顶向下动态规划解法介绍
博弈问题通常可以使用动态规划求解。这道题由于数据规模的原因,动态规划方法不适用,因此只是介绍。
使用三维数组 dp 表示状态,dp}[\textit{mouse}][\textit{cat}][\textit{turns}] 表示从老鼠位于节点 mouse、猫位于节点 cat、游戏已经进行了 turns 轮的状态开始,猫和老鼠都按照最优策略的情况下的游戏结果。假设图中的节点数是 n,则有 0 \le \textit{mouse}, \textit{cat} < n。
由于游戏的初始状态是老鼠位于节点 1,猫位于节点 2,因此 dp}[1][2][0] 为从初始状态开始的游戏结果。
动态规划的边界条件为可以直接得到游戏结果的状态,包括以下三种状态:
如果 mouse} = 0,老鼠躲入洞里,则老鼠获胜,因此对于任意 cat 和 turns 都有 dp}[0][\textit{cat}][\textit{turns}] = 1,该状态为老鼠的必胜状态,猫的必败状态。
如果 cat} = \textit{mouse,猫和老鼠占据相同的节点,则猫获胜,因此当 cat} = \textit{mouse 时,对于任意 mouse、cat 和 turns 都有 dp}[\textit{mouse}][\textit{cat}][\textit{turns}] = 2,该状态为老鼠的必败状态,猫的必胜状态。注意猫不能移动到节点 0,因此当 mouse} = 0 时,一定有 cat} \ne \textit{mouse。
如果 turns} \ge 2n(n - 1),则是平局,该状态为双方的必和状态。
由于游戏中的每个局面由老鼠的位置、猫的位置和轮到移动的一方三个因素确定,老鼠可能的位置数是 n,因此猫可能的位置数是 n - 1(由于猫不能移动到节点 0),轮到移动的一方有 2 种可能,因此游戏中所有可能的局面数是 2n(n - 1)。
根据抽屉原理可知,当游戏进行了 2n(n - 1) 轮时,一定存在至少一个猫和老鼠重复经过的局面。由于猫和老鼠都按照最优策略参与游戏,对于同一个局面,游戏结果是相同的。
考虑该重复经过的局面。从该局面开始,双方按照最优策略移动,结果只能回到该局面,任何一方都无法让己方到达必胜状态,让对方到达必败状态,因此该状态对于双方都不是必胜状态,只能是必和状态。
如果该重复经过的局面和初始局面相同,则初始局面即为双方的必和状态。如果该重复经过的局面和初始局面不同,则从初始局面开始,双方按照最优策略移动,结果只能到达双方的必和状态,任何一方都无法让己方到达必胜状态,让对方到达必败状态,因此初始局面对于双方都不是必胜状态,只能是必和状态。
综上所述,如果游戏进行了 2n(n - 1) 轮还没有任何一方获胜,则是平局。
动态规划的状态转移需要考虑当前玩家所有可能的移动,选择最优策略的移动。
由于老鼠先开始移动,猫后开始移动,因此可以根据游戏已经进行的轮数 turns 的奇偶性决定当前轮到的玩家,当 turns 是偶数时轮到老鼠移动,当 turns 是奇数时轮到猫移动。
如果轮到老鼠移动,则对于老鼠从当前节点移动一次之后可能到达的每个节点,进行如下操作:
如果存在一个节点,老鼠到达该节点之后,老鼠可以获胜,则老鼠到达该节点之后的状态为老鼠的必胜状态,猫的必败状态,因此在老鼠移动之前的当前状态为老鼠的必胜状态。
如果老鼠到达任何节点之后的状态都不是老鼠的必胜状态,但是存在一个节点,老鼠到达该节点之后,结果是平局,则老鼠到达该节点之后的状态为双方的必和状态,因此在老鼠移动之前的当前状态为双方的必和状态。
如果老鼠到达任何节点之后的状态都不是老鼠的必胜状态或必和状态,则老鼠到达任何节点之后的状态都为老鼠的必败状态,猫的必胜状态,因此在老鼠移动之前的当前状态为老鼠的必败状态。
如果轮到猫移动,则对于猫从当前节点移动一次之后可能到达的每个节点,进行如下操作:
如果存在一个节点,猫到达该节点之后,猫可以获胜,则猫到达该节点之后的状态为猫的必胜状态,老鼠的必败状态,因此在猫移动之前的当前状态为猫的必胜状态。
如果猫到达任何节点之后的状态都不是猫的必胜状态,但是存在一个节点,猫到达该节点之后,结果是平局,则猫到达该节点之后的状态为双方的必和状态,因此在猫移动之前的当前状态为双方的必和状态。
如果猫到达任何节点之后的状态都不是猫的必胜状态或必和状态,则猫到达任何节点之后的状态都为猫的必败状态,老鼠的必胜状态,因此在猫移动之前的当前状态为猫的必败状态。
实现方面,由于双方移动的策略相似,因此可以使用一个函数实现移动策略,根据游戏已经进行的轮数的奇偶性决定当前轮到的玩家。对于特定玩家的移动,实现方法如下:
如果当前玩家存在一种移动方法到达非必败状态,则用该状态更新游戏结果。
如果该移动方法到达必胜状态,则将当前状态(移动前的状态)设为必胜状态,结束遍历其他可能的移动。
如果该移动方法到达必和状态,则将当前状态(移动前的状态)设为必和状态,继续遍历其他可能的移动,因为可能存在到达必胜状态的移动方法。
如果当前玩家的任何移动方法都到达必败状态,则将当前状态(移动前的状态)设为必败状态。
由于老鼠可能的位置有 n 个,猫可能的位置有 n - 1 个,游戏轮数最大为 2n(n - 1),因此动态规划的状态数是 O(n^4),对于每个状态需要 O(n) 的时间计算状态值,因此总时间复杂度是 O(n^5),该时间复杂度会超出时间限制,因此自顶向下的动态规划不适用于这道题。以下代码为自顶向下的动态规划的实现,仅供读者参考。
1 | class Solution { |
1 | public class Solution { |
1 | const int MOUSE_WIN = 1; |
1 | DRAW = 0 |
1 | const MOUSE_WIN = 1; |
1 | const ( |
1 |
|
方法一:拓扑排序
思路和算法
自顶向下的动态规划由于判定平局的标准和轮数有关,因此时间复杂度较高。为了降低时间复杂度,需要使用自底向上的方法实现,消除结果和轮数之间的关系。
使用自底向上的方法实现时,游戏中的状态由老鼠的位置、猫的位置和轮到移动的一方三个因素确定。初始时,只有边界情况的胜负结果已知,其余所有状态的结果都初始化为平局。边界情况为直接确定胜负的情况,包括两类情况:老鼠躲入洞里,无论猫位于哪个节点,都是老鼠获胜;猫和老鼠占据相同的节点,无论占据哪个节点,都是猫获胜。
从边界情况出发遍历其他情况。对于当前状态,可以得到老鼠的位置、猫的位置和轮到移动的一方,根据当前状态可知上一轮的所有可能状态,其中上一轮的移动方和当前的移动方相反,上一轮的移动方在上一轮状态和当前状态所在的节点不同。假设当前状态是老鼠所在节点是 mouse,猫所在节点是 cat,则根据当前的移动方,可以得到上一轮的所有可能状态:
如果当前的移动方是老鼠,则上一轮的移动方是猫,上一轮状态中老鼠所在节点是 mouse,猫所在节点可能是 graph}[\textit{cat}] 中的任意一个节点(除了节点 0);
如果当前的移动方是猫,则上一轮的移动方是老鼠,上一轮状态中老鼠所在节点可能是 graph}[\textit{mouse}] 中的任意一个节点,猫所在节点是 cat。
对于上一轮的每一种可能的状态,如果该状态的结果已知不是平局,则不需要重复计算该状态的结果,只有对结果是平局的状态,才需要计算该状态的结果。对于上一轮的移动方,只有当可以确定上一轮状态是必胜状态或者必败状态时,才更新上一轮状态的结果。
如果上一轮的移动方和当前状态的结果的获胜方相同,由于当前状态为上一轮的移动方的必胜状态,因此上一轮的移动方一定可以移动到当前状态而获胜,上一轮状态为上一轮的移动方的必胜状态。
如果上一轮的移动方和当前状态的结果的获胜方不同,则上一轮的移动方需要尝试其他可能的移动,可能有以下三种情况:
如果存在一种移动可以到达上一轮的移动方的必胜状态,则上一轮状态为上一轮的移动方的必胜状态;
如果所有的移动都到达上一轮的移动方的必败状态,则上一轮状态为上一轮的移动方的必败状态;
如果所有的移动都不能到达上一轮的移动方的必胜状态,但是存在一种移动可以到达上一轮的移动方的必和状态,则上一轮状态为上一轮的移动方的必和状态。
其中,对于必败状态与必和状态的判断依据为上一轮的移动方可能的移动是都到达必败状态还是可以到达必和状态。为了实现必败状态与必和状态的判断,需要记录每个状态的度,初始时每个状态的度为当前玩家在当前位置可以移动到的节点数。对于老鼠而言,初始的度为老鼠所在的节点的相邻节点数;对于猫而言,初始的度为猫所在的节点的相邻且非节点 0 的节点数。
遍历过程中,从当前状态出发遍历上一轮的所有可能状态,如果上一轮状态的结果是平局且上一轮的移动方和当前状态的结果的获胜方不同,则将上一轮状态的度减 1。如果上一轮状态的度减少到 0,则从上一轮状态出发到达的所有状态都是上一轮的移动方的必败状态,因此上一轮状态也是上一轮的移动方的必败状态。
在确定上一轮状态的结果(必胜或必败)之后,即可从上一轮状态出发,遍历其他结果是平局的状态。当没有更多的状态可以确定胜负结果时,遍历结束,此时即可得到初始状态的结果。
细心的读者可以发现,上述遍历的过程其实是拓扑排序。
证明
必胜状态和必败状态都符合博弈中的最优策略,需要证明的是必和状态的正确性。
遍历结束之后,如果一个状态的结果是平局,则该状态满足以下两个条件:
从该状态出发,任何移动都无法到达该状态的移动方的必胜状态;
从该状态出发,存在一种移动可以到达必和状态。
对于标记结果是平局的状态,如果其实际结果是该状态的移动方必胜,则一定存在一个下一轮状态,为当前状态的移动方的必胜状态,在根据下一轮状态的结果标记当前状态的结果时会将当前状态标记为当前状态的移动方的必胜状态,和标记结果是平局矛盾。
对于标记结果是平局的状态,如果其实际结果是该状态的移动方必败,则所有的下一轮状态都为当前状态的移动方的必败状态,在根据下一轮状态的结果标记当前状态的结果时会将当前状态标记为当前状态的移动方的必败状态,和标记结果是平局矛盾。
因此,如果标记的状态是必和状态,则实际结果一定是必和状态。
代码
1 | class Solution { |
1 | public class Solution { |
1 | class Solution { |
1 | MOUSE_TURN = 0 |
1 | const MOUSE_TURN = 0, CAT_TURN = 1; |
1 | const ( |
复杂度分析
时间复杂度:O(n^3),其中 n 是图中的节点数。状态数是 O(n^2),对于每个状态需要 O(n) 的时间计算状态值,因此总时间复杂度是 O(n^3)。
空间复杂度:O(n^2),其中 n 是图中的节点数。需要记录每个状态的度和结果,状态数是 O(n^2)。