0919-完全二叉树插入器

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:31 2023-09-13 16:06:31 Updated    

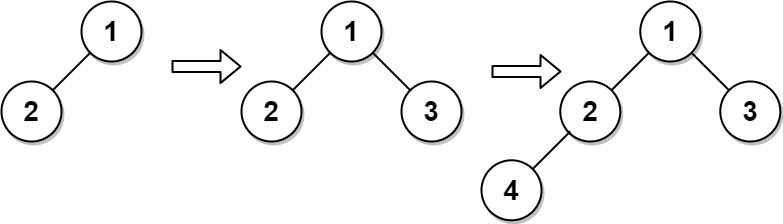
完全二叉树 是每一层（除最后一层外）都是完全填充（即，节点数达到最大）的，并且所有的节点都尽可能地集中在左侧。

设计一种算法，将一个新节点插入到一个完整的二叉树中，并在插入后保持其完整。

实现 CBTInserter 类:

  • CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构；
  • CBTInserter.insert(int v) 向树中插入一个值为 Node.val == val的新节点 TreeNode。使树保持完全二叉树的状态， 并返回插入节点 TreeNode 的父节点的值 ；
  • CBTInserter.get_root() 将返回树的头节点。

示例 1：

**输入**
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
**输出**
[null, 1, 2, [1, 2, 3, 4]]

**解释**
CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3);  // 返回 1
cBTInserter.insert(4);  // 返回 2
cBTInserter.get_root(); // 返回 [1, 2, 3, 4]

提示：

  • 树中节点数量范围为 [1, 1000]
  • 0 <= Node.val <= 5000
  • root 是完全二叉树
  • 0 <= val <= 5000
  • 每个测试用例最多调用 insert 和 get_root 操作 104 次

方法一：队列

思路与算法

对于一棵完全二叉树而言，其除了最后一层之外都是完全填充的，并且最后一层的节点全部在最左侧。那么，只有倒数第二层（如果存在）最右侧的若干个节点，以及最后一层的全部节点可以再添加子节点，其余的节点都已经拥有两个子节点。

因此，我们可以使用一个队列存储上述提到的这些可以添加子节点的节点。队列中的存储顺序为：首先「从左往右」存储倒数第二层最右侧的节点，再「从左往右」存储最后一层的全部节点。这一步可以使用广度优先搜索来完成，因为广度优先搜索就是按照层优先进行遍历的。

随后，当我们每次调用 insert(val) 时，我们就创建出一个节点 child，并将它作为队列的队首节点的子节点。在这之后，我们需要把 child 加入队尾，并且如果对队首节点已经有两个子节点，我们需要将其从队列中移除。

代码

[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class CBTInserter {
public:
    CBTInserter(TreeNode* root) {
        this->root = root;

        queue<TreeNode*> q;
        q.push(root);
        
        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();
            if (node->left) {
                q.push(node->left);
            }
            if (node->right) {
                q.push(node->right);
            }
            if (!(node->left && node->right)) {
                candidate.push(node);
            }
        }
    }
    
    int insert(int val) {
        TreeNode* child = new TreeNode(val);
        TreeNode* node = candidate.front();
        int ret = node->val;
        if (!node->left) {
            node->left = child;
        }
        else {
            node->right = child;
            candidate.pop();
        }
        candidate.push(child);
        return ret;
    }
    
    TreeNode* get_root() {
        return root;
    }

private:
    queue<TreeNode*> candidate;
    TreeNode* root;
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class CBTInserter {
    Queue<TreeNode> candidate;
    TreeNode root;

    public CBTInserter(TreeNode root) {
        this.candidate = new ArrayDeque<TreeNode>();
        this.root = root;

        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
            if (!(node.left != null && node.right != null)) {
                candidate.offer(node);
            }
        }
    }

    public int insert(int val) {
        TreeNode child = new TreeNode(val);
        TreeNode node = candidate.peek();
        int ret = node.val;
        if (node.left == null) {
            node.left = child;
        } else {
            node.right = child;
            candidate.poll();
        }
        candidate.offer(child);
        return ret;
    }

    public TreeNode get_root() {
        return root;
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class CBTInserter {
    Queue<TreeNode> candidate;
    TreeNode root;

    public CBTInserter(TreeNode root) {
        this.candidate = new Queue<TreeNode>();
        this.root = root;

        Queue<TreeNode> queue = new Queue<TreeNode>();
        queue.Enqueue(root);

        while (queue.Count > 0) {
            TreeNode node = queue.Dequeue();
            if (node.left != null) {
                queue.Enqueue(node.left);
            }
            if (node.right != null) {
                queue.Enqueue(node.right);
            }
            if (!(node.left != null && node.right != null)) {
                candidate.Enqueue(node);
            }
        }
    }

    public int Insert(int val) {
        TreeNode child = new TreeNode(val);
        TreeNode node = candidate.Peek();
        int ret = node.val;
        if (node.left == null) {
            node.left = child;
        } else {
            node.right = child;
            candidate.Dequeue();
        }
        candidate.Enqueue(child);
        return ret;
    }

    public TreeNode Get_root() {
        return root;
    }
}
[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class CBTInserter:

    def __init__(self, root: TreeNode):
        self.root = root
        self.candidate = deque()

        q = deque([root])
        while q:
            node = q.popleft()
            if node.left:
                q.append(node.left)
            if node.right:
                q.append(node.right)
            if not (node.left and node.right):
                self.candidate.append(node)

    def insert(self, val: int) -> int:
        candidate_ = self.candidate

        child = TreeNode(val)
        node = candidate_[0]
        ret = node.val
        
        if not node.left:
            node.left = child
        else:
            node.right = child
            candidate_.popleft()
        
        candidate_.append(child)
        return ret

    def get_root(self) -> TreeNode:
        return self.root
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
typedef struct DLinkListNode {
    struct TreeNode *val;
    struct DLinkListNode *prev, *next;
} DLinkListNode;

typedef struct {
    DLinkListNode *head, *tail;
    int size;
} Deque;

DLinkListNode * dLinkListNodeCreat(struct TreeNode* val) {
    DLinkListNode *obj = (DLinkListNode *)malloc(sizeof(DLinkListNode));
    obj->val = val;
    obj->prev = NULL;
    obj->next = NULL;
    return obj;
} 

Deque* dequeCreate() {
    Deque *obj = (Deque *)malloc(sizeof(Deque));
    obj->size = 0;
    obj->head = obj->tail = NULL;
    return obj;
}

bool dequeInsertFront(Deque* obj, struct TreeNode* value) {
    DLinkListNode *node = dLinkListNodeCreat(value);
    if (obj->size == 0) {
        obj->head = obj->tail = node;
    } else {
        node->next = obj->head;
        obj->head->prev = node;
        obj->head = node;
    }
    obj->size++;
    return true;
}

bool dequeInsertLast(Deque* obj, struct TreeNode* value) {
    DLinkListNode *node = dLinkListNodeCreat(value);
    if (obj->size == 0) {
        obj->head = obj->tail = node;
    } else {
        obj->tail->next = node;
        node->prev = obj->tail;
        obj->tail = node;
    }
    obj->size++;
    return true;
}

bool dequeDeleteFront(Deque* obj) {
    if (obj->size == 0) {
        return false;
    }
    DLinkListNode *node = obj->head;
    obj->head = obj->head->next;
    if (obj->head) {
        obj->head->prev = NULL;
    }
    free(node);
    obj->size--;
    return true;
}

bool dequeDeleteLast(Deque* obj) {
    if (obj->size == 0) {
        return false;
    }
    DLinkListNode *node = obj->tail;
    obj->tail = obj->tail->prev;
    if (obj->tail) {
        obj->tail->next = NULL;
    }
    free(node);
    obj->size--;
    return true;
}

struct TreeNode* dequeGetFront(Deque* obj) {
    if (obj->size == 0) {
        return NULL;
    }
    return obj->head->val;
}

struct TreeNode* dequeGetRear(Deque* obj) {
    if (obj->size == 0) {
        return NULL;
    }
    return obj->tail->val;
}

bool dequeIsEmpty(Deque* obj) {
    return obj->size == 0;
}

void dequeFree(Deque* obj) {
    for (DLinkListNode *curr = obj->head; curr;) {
        DLinkListNode *node = curr;
        curr = curr->next;
        free(node);
    }
    free(obj);
}

typedef struct {
    Deque* candidate;
    struct TreeNode* root;
} CBTInserter;


CBTInserter* cBTInserterCreate(struct TreeNode* root) {
    CBTInserter *obj = (CBTInserter *)malloc(sizeof(CBTInserter));
    obj->candidate = dequeCreate();
    obj->root = root;
    Deque *q = dequeCreate();
    dequeInsertLast(q, root);
    while (!dequeIsEmpty(q)) {
        struct TreeNode* node = dequeGetFront(q);
        dequeDeleteFront(q);
        if (node->left) {
            dequeInsertLast(q, node->left);
        }
        if (node->right) {
            dequeInsertLast(q, node->right);
        }
        if (!(node->left && node->right)) {
            dequeInsertLast(obj->candidate, node);
        }
    }
    return obj;
}

int cBTInserterInsert(CBTInserter* obj, int val) {
    struct TreeNode* child = (struct TreeNode *)malloc(sizeof(struct TreeNode));
    child->val = val;
    child->left = NULL;
    child->right = NULL;
    struct TreeNode* node = dequeGetFront(obj->candidate);
    int ret = node->val;
    if (!node->left) {
        node->left = child;
    } else {
        node->right = child;
        dequeDeleteFront(obj->candidate);
    }
    dequeInsertLast(obj->candidate, child);
    return ret;
}

struct TreeNode* cBTInserterGet_root(CBTInserter* obj) {
    return obj->root;
}

void cBTInserterFree(CBTInserter* obj) {
    dequeFree(obj->candidate);
    free(obj);
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
type CBTInserter struct {
    root      *TreeNode
    candidate []*TreeNode
}

func Constructor(root *TreeNode) CBTInserter {
    q := []*TreeNode{root}
    candidate := []*TreeNode{}
    for len(q) > 0 {
        node := q[0]
        q = q[1:]
        if node.Left != nil {
            q = append(q, node.Left)
        }
        if node.Right != nil {
            q = append(q, node.Right)
        }
        if node.Left == nil || node.Right == nil {
            candidate = append(candidate, node)
        }
    }
    return CBTInserter{root, candidate}
}

func (c *CBTInserter) Insert(val int) int {
    child := &TreeNode{Val: val}
    node := c.candidate[0]
    if node.Left == nil {
        node.Left = child
    } else {
        node.Right = child
        c.candidate = c.candidate[1:]
    }
    c.candidate = append(c.candidate, child)
    return node.Val
}

func (c *CBTInserter) Get_root() *TreeNode {
    return c.root
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var CBTInserter = function(root) {
    this.candidate = [];
    this.root = root;

    const queue = [];
    queue.push(root);

    while (queue.length) {
        const node = queue.shift();
        if (node.left) {
            queue.push(node.left);
        }
        if (node.right) {
            queue.push(node.right);
        }
        if (!(node.left && node.right)) {
            this.candidate.push(node);
        }
    }
};

CBTInserter.prototype.insert = function(val) {
    const child = new TreeNode(val);
    const node = this.candidate[0];
    let ret = node.val;
    if (!node.left) {
        node.left = child;
    } else {
        node.right = child;
        this.candidate.shift();
    }
    this.candidate.push(child);
    return ret;
};

CBTInserter.prototype.get_root = function() {
    return this.root;
};

复杂度分析

  • 时间复杂度：初始化 CBTInserter(root) 需要的时间为 O(n)，其中 n 是给定的初始完全二叉树的节点个数。insert(v) 和 get_root() 的时间复杂度均为 O(1)。

  • 空间复杂度：O(n+q)，其中 q 是 insert(v) 的调用次数。在调用了 q 次 insert(v) 后，完全二叉树中有 n+q 个节点，其中有一半的节点在队列中，需要 O(n+q) 的空间。

方法二：二进制表示

思路与算法

如果我们将完全二叉树的每个节点进行编号，其中：

  • 根节点的编号为 1；

  • 如果某个节点的编号为 x，那么其左子节点的编号为 2x，右子节点的编号为 2x+1。

那么我们可以发现，按照广度优先搜索的顺序，完全二叉树中的所有节点的编号是连续的。这可以用二进制表示看出：完全二叉树的第 i (i \geq 1) 层有 2^{i-1 个节点，它们的编号恰好对应着 i 位的二进制表示，共有 2^{i-1 个（最高位必须为 1）。当某个节点编号为 x 时，左子节点的编号 2x 即为将 x 的二进制表示左移一位后在最低位补 0，右子节点的编号即为将 x 的二进制表示右移一位后在最低位补 1。

因此，在初始化时，我们只需要使用深度优先搜索或者广度优先搜索，得到初始完全二叉树中的节点个数。在调用 insert(v) 时，我们可以知道它的编号 x，那么就可以从高到低遍历 x 的每一个二进制位（忽略最高位的 1），如果为 0 就往左子节点移动，否则往右子节点移动，这样就可以到达节点需要被插入的位置。

代码

[sol2-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
class CBTInserter {
public:
    CBTInserter(TreeNode* root) {
        this->root = root;

        queue<TreeNode*> q;
        q.push(root);
        
        while (!q.empty()) {
            ++cnt;
            TreeNode* node = q.front();
            q.pop();
            if (node->left) {
                q.push(node->left);
            }
            if (node->right) {
                q.push(node->right);
            }
        }
    }
    
    int insert(int val) {
        ++cnt;
        TreeNode* child = new TreeNode(val);
        TreeNode* node = root;
        int highbit = 31 - __builtin_clz(cnt);
        for (int i = highbit - 1; i >= 1; --i) {
            if (cnt & (1 << i)) {
                node = node->right;
            }
            else {
                node = node->left;
            }
        }
        if (cnt & 1) {
            node->right = child;
        }
        else {
            node->left = child;
        }
        return node->val;
    }
    
    TreeNode* get_root() {
        return root;
    }

private:
    int cnt = 0;
    TreeNode* root;
};
[sol2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class CBTInserter {
    int cnt;
    TreeNode root;

    public CBTInserter(TreeNode root) {
        this.cnt = 0;
        this.root = root;

        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            ++cnt;
            TreeNode node = queue.poll();
            if (node.left != null) {
                queue.offer(node.left);
            }
            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

    public int insert(int val) {
        ++cnt;
        TreeNode child = new TreeNode(val);
        TreeNode node = root;
        int highbit = 31 - Integer.numberOfLeadingZeros(cnt);
        for (int i = highbit - 1; i >= 1; --i) {
            if ((cnt & (1 << i)) != 0) {
                node = node.right;
            } else {
                node = node.left;
            }
        }
        if ((cnt & 1) != 0) {
            node.right = child;
        } else {
            node.left = child;
        }
        return node.val;
    }

    public TreeNode get_root() {
        return root;
    }
}
[sol2-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class CBTInserter:

    def __init__(self, root: TreeNode):
        self.root = root
        self.cnt = 0

        q = deque([root])
        while q:
            self.cnt += 1
            node = q.popleft()
            if node.left:
                q.append(node.left)
            if node.right:
                q.append(node.right)

    def insert(self, val: int) -> int:
        self.cnt += 1

        child = TreeNode(val)
        node = self.root
        highbit = self.cnt.bit_length() - 1

        for i in range(highbit - 1, 0, -1):
            if self.cnt & (1 << i):
                node = node.right
            else:
                node = node.left
        
        if self.cnt & 1:
            node.right = child
        else:
            node.left = child
        
        return node.val

    def get_root(self) -> TreeNode:
        return self.root
[sol2-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#define MAX_NODE_SIZE 1000

typedef struct {
    int cnt;
    struct TreeNode* root;
} CBTInserter;

CBTInserter* cBTInserterCreate(struct TreeNode* root) {
    CBTInserter *obj = (CBTInserter *)malloc(sizeof(CBTInserter));
    obj->root = root;
    obj->cnt = 0;
    struct TreeNode **queue = (struct TreeNode **)malloc(sizeof(struct TreeNode *) * MAX_NODE_SIZE);
    int head = 0, tail = 0;
    queue[tail++] = root;
    while (head != tail) {
        ++obj->cnt;
        struct TreeNode* node = queue[head++];
        if (node->left) {
            queue[tail++] = node->left;
        }
        if (node->right) {
            queue[tail++] = node->right;
        }
    }
    free(queue);
    return obj;
}

int cBTInserterInsert(CBTInserter* obj, int val) {
    ++obj->cnt;
    struct TreeNode* child = (struct TreeNode*)malloc(sizeof(struct TreeNode));
    child->val = val;
    child->left = NULL;
    child->right = NULL;
    struct TreeNode* node = obj->root;
    int highbit = 31 - __builtin_clz(obj->cnt);
    for (int i = highbit - 1; i >= 1; --i) {
        if (obj->cnt & (1 << i)) {
            node = node->right;
        }
        else {
            node = node->left;
        }
    }
    if (obj->cnt & 1) {
        node->right = child;
    }
    else {
        node->left = child;
    }
    return node->val;
}

struct TreeNode* cBTInserterGet_root(CBTInserter* obj) {
    return obj->root;
}

void cBTInserterFree(CBTInserter* obj) {
    free(obj);
}
[sol2-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
type CBTInserter struct {
    root *TreeNode
    cnt  int
}

func Constructor(root *TreeNode) CBTInserter {
    q := []*TreeNode{root}
    cnt := 0
    for len(q) > 0 {
        cnt++
        node := q[0]
        q = q[1:]
        if node.Left != nil {
            q = append(q, node.Left)
        }
        if node.Right != nil {
            q = append(q, node.Right)
        }
    }
    return CBTInserter{root, cnt}
}

func (c *CBTInserter) Insert(val int) int {
    c.cnt++
    child := &TreeNode{Val: val}
    node := c.root
    for i := bits.Len(uint(c.cnt)) - 2; i > 0; i-- {
        if c.cnt>>i&1 == 0 {
            node = node.Left
        } else {
            node = node.Right
        }
    }
    if c.cnt&1 == 0 {
        node.Left = child
    } else {
        node.Right = child
    }
    return node.Val
}

func (c *CBTInserter) Get_root() *TreeNode {
    return c.root
}
[sol2-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
var CBTInserter = function(root) {
    this.cnt = 0;
    this.root = root;

    const queue = [];
    queue.push(root);
    
    while (queue.length) {
        ++this.cnt;
        const node = queue.shift();
        if (node.left) {
            queue.push(node.left);
        }
        if (node.right) {
            queue.push(node.right);
        }
    }
};

CBTInserter.prototype.insert = function(val) {
    ++this.cnt;
    const child = new TreeNode(val);
    let node = this.root;
    const highbit = ('' + this.cnt.toString(2)).length - 1;
    for (let i = highbit - 1; i >= 1; --i) {
        if ((this.cnt & (1 << i)) !== 0) {
            node = node.right;
        } else {
            node = node.left;
        }
    }
    if ((this.cnt & 1) !== 0) {
        node.right = child;
    } else {
        node.left = child;
    }
    return node.val;
};

CBTInserter.prototype.get_root = function() {
    return this.root;
};

复杂度分析

  • 时间复杂度：初始化 CBTInserter(root) 需要的时间为 O(n)，其中 n 是给定的初始完全二叉树的节点个数。这里也可以通过 222. 完全二叉树的节点个数 中的方法优化到 O(\log^2 n)。insert(v) 需要的时间为 O(\log (n+q))，其中 q 是 insert(v) 的调用次数。get_root() 的时间复杂度为 O(1)。

  • 空间复杂度：初始化 CBTInserter(root) 需要的空间为 O(n)。如果使用优化方法，空间可以降低到 O(\log n)。其它所有函数调用都只需要 O(1) 的空间。

 Comments
On this page
0919-完全二叉树插入器