给你一个 n x n 的 方形 整数数组 matrix ,请你找出并返回通过 matrix 的 下降路径 __ 的
****最小和 。
下降路径
可以从第一行中的任何元素开始,并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列(即位于正下方或者沿对角线向左或者向右的第一个元素)。具体来说,位置
(row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 `(row + 1, col
示例 1:

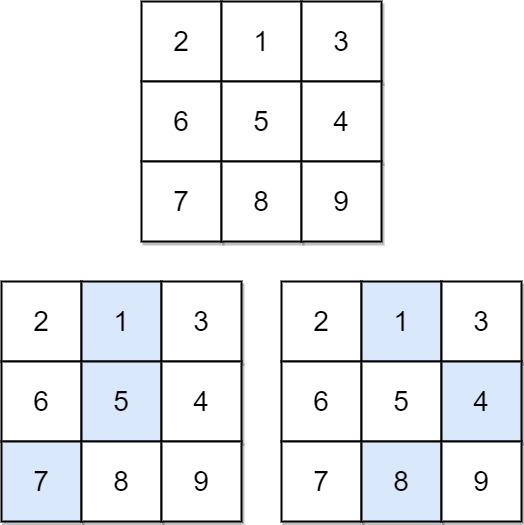
**输入:** matrix = [[2,1,3],[6,5,4],[7,8,9]]
**输出:** 13
**解释:** 如图所示,为和最小的两条下降路径
示例 2:

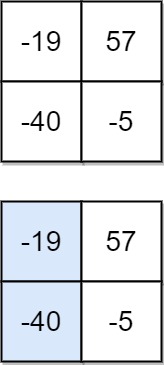
**输入:** matrix = [[-19,57],[-40,-5]]
**输出:** -59
**解释:** 如图所示,为和最小的下降路径
提示:
n == matrix.length == matrix[i].length1 <= n <= 100-100 <= matrix[i][j] <= 100
方法一:动态规划
思路
题目需要求出矩阵的和最小下降路径,可以求出末行每个元素的和最小下降路径,然后找到其中和最小的那一条路径即可。而根据题意,每个坐标仅可以通过它的上一排紧邻的三个坐标到达(左上,正上,右上),根据贪心思想,每个坐标的和最小下降路径长度即为它的上一排紧邻的三个坐标的和最小下降路径长度的最小值,再加上当前坐标的和。用 dp 表示和最小下降路径长度的话,即为 dp}[i][j] = \textit{matrix}[i][j] + \min(\textit{dp}[i-1][j-1], \textit{dp}[i-1][j], \textit{dp}[i-1][j+1]),第一列和最后一列有边界情况,需要特殊处理。而第一行每个元素的和最小下降路径长度为它们本身的值。最后返回最后一行的和最小下降路径长度的最小值即可。
代码
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
dp = [matrix[0]]
n = len(matrix)
for i in range(1, n):
cur = [0] * n
for j in range(n):
mn = dp[-1][j]
if j > 0:
mn = min(mn, dp[-1][j - 1])
if j < n - 1:
mn = min(mn, dp[-1][j + 1])
cur[j] = mn + matrix[i][j]
dp.append(cur)
return min(dp[-1])
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| class Solution {
public int minFallingPathSum(int[][] matrix) {
int n = matrix.length;
int[][] dp = new int[n][n];
System.arraycopy(matrix[0], 0, dp[0], 0, n);
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
int mn = dp[i - 1][j];
if (j > 0) {
mn = Math.min(mn, dp[i - 1][j - 1]);
}
if (j < n - 1) {
mn = Math.min(mn, dp[i - 1][j + 1]);
}
dp[i][j] = mn + matrix[i][j];
}
}
return Arrays.stream(dp[n - 1]).min().getAsInt();
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| public class Solution {
public int MinFallingPathSum(int[][] matrix) {
int n = matrix.Length;
int[][] dp = new int[n][];
for (int i = 0; i < n; i++) {
dp[i] = new int[n];
}
Array.Copy(matrix[0], 0, dp[0], 0, n);
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
int mn = dp[i - 1][j];
if (j > 0) {
mn = Math.Min(mn, dp[i - 1][j - 1]);
}
if (j < n - 1) {
mn = Math.Min(mn, dp[i - 1][j + 1]);
}
dp[i][j] = mn + matrix[i][j];
}
}
return dp[n - 1].Min();
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public:
int minFallingPathSum(vector<vector<int>>& matrix) {
int n = matrix.size();
vector<vector<int>> dp(n, vector<int>(n));
copy(matrix[0].begin(), matrix[0].end(), dp[0].begin());
for (int i = 1; i < n; i++) {
for (int j = 0; j < n; j++) {
int mn = dp[i - 1][j];
if (j > 0) {
mn = min(mn, dp[i - 1][j - 1]);
}
if (j < n - 1) {
mn = min(mn, dp[i - 1][j + 1]);
}
dp[i][j] = mn + matrix[i][j];
}
}
return *min_element(dp[n - 1].begin(), dp[n - 1].end());
}
};
|
[sol1-Go]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| func minFallingPathSum(matrix [][]int) int {
n := len(matrix)
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, n)
}
copy(dp[0], matrix[0])
for i := 1; i < n; i++ {
for j := 0; j < n; j++ {
mn := dp[i - 1][j]
if j > 0 {
mn = min(mn, dp[i - 1][j - 1])
}
if j < n - 1 {
mn = min(mn, dp[i - 1][j + 1])
}
dp[i][j] = mn + matrix[i][j]
}
}
minVal := dp[n-1][0]
for _, val := range dp[n-1] {
if val < minVal {
minVal = val
}
}
return minVal
}
func min(a, b int) int {
if a < b {
return a
}
return b
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| var minFallingPathSum = function(matrix) {
const n = matrix.length;
const dp = new Array(n).fill(0).map(() => new Array(n).fill(0));
dp[0] = [...matrix[0]];
for (let i = 1; i < n; i++) {
for (let j = 0; j < n; j++) {
let mn = dp[i - 1][j];
if (j > 0) {
mn = Math.min(mn, dp[i - 1][j - 1]);
}
if (j < n - 1) {
mn = Math.min(mn, dp[i - 1][j + 1]);
}
dp[i][j] = mn + matrix[i][j];
}
}
return Math.min(...dp[n - 1]);
}
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| int min(int a, int b) {
return a < b ? a : b;
}
int minFallingPathSum(int** matrix, int matrixSize, int* matrixColSize) {
int n = matrixSize, m = *matrixColSize;
int** dp = (int**)malloc(n * sizeof(int*));
for (int i = 0; i < n; i++) {
dp[i] = (int*)malloc(m * sizeof(int));
}
for (int i = 0; i < n; i++) {
dp[0][i] = matrix[0][i];
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < m; j++) {
int mn = dp[i - 1][j];
if (j > 0) {
mn = min(mn, dp[i - 1][j - 1]);
}
if (j < m - 1) {
mn = min(mn, dp[i - 1][j + 1]);
}
dp[i][j] = mn + matrix[i][j];
}
}
int minVal = INT_MAX;
for (int i = 0; i < n; i++) {
if (dp[n - 1][i] < minVal) {
minVal = dp[n - 1][i];
}
}
for (int i = 0; i < n; i++) {
free(dp[i]);
}
free(dp);
return minVal;
}
|
复杂度分析