0935-骑士拨号器

象棋骑士有一个 独特的移动方式 ，它可以垂直移动两个方格，水平移动一个方格，或者水平移动两个方格，垂直移动一个方格(两者都形成一个 **L
**的形状)。

象棋骑士可能的移动方式如下图所示:

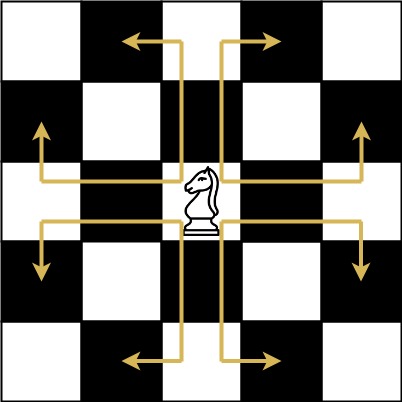
我们有一个象棋骑士和一个电话垫，如下所示，骑士 只能站在一个数字单元格上 (即蓝色单元格)。

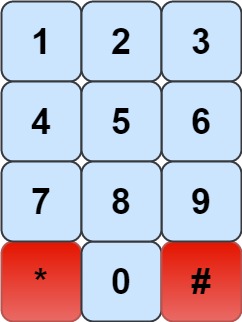
给定一个整数 n，返回我们可以拨多少个长度为 n 的不同电话号码。

你可以将骑士放置在 任何数字单元格 上，然后你应该执行 n - 1 次移动来获得长度为 n 的号码。所有的跳跃应该是 有效 的骑士跳跃。

因为答案可能很大， **所以输出答案模 **109 + 7.

示例 1：

**输入：** n = 1
**输出：** 10
**解释：** 我们需要拨一个长度为1的数字，所以把骑士放在10个单元格中的任何一个数字单元格上都能满足条件。

示例 2：

**输入：** n = 2
**输出：** 20
**解释：** 我们可以拨打的所有有效号码为[04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]

示例 3：

**输入：** n = 3131
**输出：** 136006598
**解释：** 注意取模

提示：

• 1 <= n <= 5000

方法一：动态规划

我们用 f(start, n) 表示骑士从数字 start 开始，跳了 n - 1 步得到不同的 n 位数字的个数。f(start, n) 可以从 f(x, n - 1) 转移而来，其中 x 是任意一个可以一步跳到 start 的数字。例如当 start = 1，时，x 可以为 6 或 8，因此有 f(1, n) = f(6, n - 1) + f(8, n - 1)。

最终的答案即为 f(0, N) + f(1, N) + ... + f(9, N)。我们可以使用滚动数组减少空间复杂度，这是因为 f(start, n) 只和 f(x, n - 1) 有关，因此在计算 f(start, n) 时，所有第二维小于 n - 1 的 f 值都不必存储。也就是说，我们只要实时存储当前正在计算的所有 f 值（n 位数字）以及上一个状态的 f 值（n - 1 位数字）即可。在 Java 代码中，我们使用 dp[0][start] 和 dp[1][start] 交替表示当前和上一个状态的 f 值。在 Python 代码中，我们使用 dp2 数组计算出当前的 f 值后，直接覆盖存储了上一个状态的 f 值的 dp 数组。

[sol1]

class Solution {
    public int knightDialer(int N) {
        int MOD = 1_000_000_007;
        int[][] moves = new int[][]{
            {4,6},{6,8},{7,9},{4,8},{3,9,0},
            {},{1,7,0},{2,6},{1,3},{2,4}};

        int[][] dp = new int[2][10];
        Arrays.fill(dp[0], 1);
        for (int hops = 0; hops < N-1; ++hops) {
            Arrays.fill(dp[~hops & 1], 0);
            for (int node = 0; node < 10; ++node)
                for (int nei: moves[node]) {
                    dp[~hops & 1][nei] += dp[hops & 1][node];
                    dp[~hops & 1][nei] %= MOD;
                }
        }

        long ans = 0;
        for (int x: dp[~N & 1])
            ans += x;
        return (int) (ans % MOD);
    }
}

[sol1]

class Solution(object):
    def knightDialer(self, N):
        MOD = 10**9 + 7
        moves = [[4,6],[6,8],[7,9],[4,8],[3,9,0],[],
                     [1,7,0],[2,6],[1,3],[2,4]]

        dp = [1] * 10
        for hops in xrange(N-1):
            dp2 = [0] * 10
            for node, count in enumerate(dp):
                for nei in moves[node]:
                    dp2[nei] += count
                    dp2[nei] %= MOD
            dp = dp2
        return sum(dp) % MOD

复杂度分析

• 时间复杂度：O(N)。

• 空间复杂度：如果使用滚动数组，则空间复杂度为 O(1)，也可以看成 O(10)。否则空间复杂度为 O(N)。