0941-有效的山脉数组

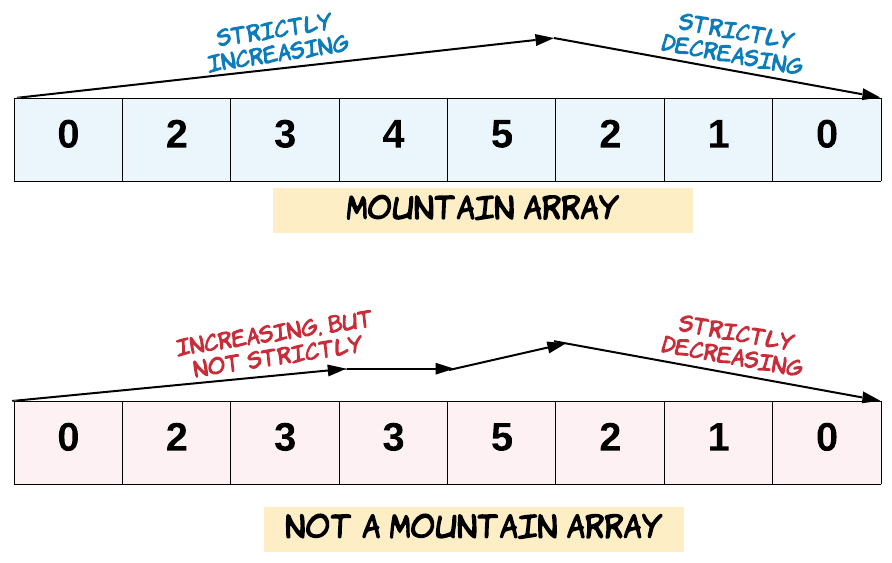
给定一个整数数组 arr，如果它是有效的山脉数组就返回 true，否则返回 false。

让我们回顾一下，如果 arr 满足下述条件，那么它是一个山脉数组：

• arr.length >= 3
• 在 0 < i < arr.length - 1 条件下，存在 i 使得：
  • arr[0] < arr[1] < ... arr[i-1] < arr[i]
  • arr[i] > arr[i+1] > ... > arr[arr.length - 1]

示例 1：

**输入：** arr = [2,1]
**输出：** false

示例 2：

**输入：** arr = [3,5,5]
**输出：** false

示例 3：

**输入：** arr = [0,3,2,1]
**输出：** true

提示：

• 1 <= arr.length <= 104
• 0 <= arr[i] <= 104

方法一：线性扫描

按题意模拟即可。我们从数组的最左侧开始向右扫描，直到找到第一个不满足 arr}[i] < \textit{arr}[i + 1] 的下标 i，那么 i 就是这个数组的最高点的下标。如果 i = 0 或者不存在这样的 i（即整个数组都是单调递增的），那么就返回 false。否则从 i 开始继续向右扫描，判断接下来的的下标 j 是否都满足 arr}[j] > \textit{arr}[j + 1]，若都满足就返回 true，否则返回 false。

[sol1-Java]

class Solution {
    public boolean validMountainArray(int[] arr) {
        int N = arr.length;
        int i = 0;

        // 递增扫描
        while (i + 1 < N && arr[i] < arr[i + 1]) {
            i++;
        }

        // 最高点不能是数组的第一个位置或最后一个位置
        if (i == 0 || i == N - 1) {
            return false;
        }

        // 递减扫描
        while (i + 1 < N && arr[i] > arr[i + 1]) {
            i++;
        }

        return i == N - 1;
    }
}

[sol1-Python3]

class Solution:
    def validMountainArray(self, arr: List[int]) -> bool:
        N = len(arr)
        i = 0

        # 递增扫描
        while i + 1 < N and arr[i] < arr[i + 1]:
            i += 1

        # 最高点不能是数组的第一个位置或最后一个位置
        if i == 0 or i == N - 1:
            return False

        # 递减扫描
        while i + 1 < N and arr[i] > arr[i + 1]:
            i += 1

        return i == N - 1

[sol1-C++]

class Solution {
public:
    bool validMountainArray(vector<int>& arr) {
        int N = arr.size();
        int i = 0;

        // 递增扫描
        while (i + 1 < N && arr[i] < arr[i + 1]) {
            i++;
        }

        // 最高点不能是数组的第一个位置或最后一个位置
        if (i == 0 || i == N - 1) {
            return false;
        }

        // 递减扫描
        while (i + 1 < N && arr[i] > arr[i + 1]) {
            i++;
        }

        return i == N - 1;
    }
};

[sol1-JavaScript]

var validMountainArray = function(arr) {
    const N = arr.length;
    let i = 0;

    // 递增扫描
    while (i + 1 < N && arr[i] < arr[i + 1]) {
        i++;
    }

    // 最高点不能是数组的第一个位置或最后一个位置
    if (i === 0 || i === N - 1) {
        return false;
    }

    // 递减扫描
    while (i + 1 < N && arr[i] > arr[i + 1]) {
        i++;
    }

    return i === N - 1;
};

[sol1-Golang]

func validMountainArray(arr []int) bool {
    i, n := 0, len(arr)

    // 递增扫描
    for ; i+1 < n && arr[i] < arr[i+1]; i++ {
    }

    // 最高点不能是数组的第一个位置或最后一个位置
    if i == 0 || i == n-1 {
        return false
    }

    // 递减扫描
    for ; i+1 < n && arr[i] > arr[i+1]; i++ {
    }

    return i == n-1
}

[sol1-C]

bool validMountainArray(int* arr, int arrSize) {
    int i = 0;

    // 递增扫描
    while (i + 1 < arrSize && arr[i] < arr[i + 1]) {
        i++;
    }

    // 最高点不能是数组的第一个位置或最后一个位置
    if (i == 0 || i == arrSize - 1) {
        return false;
    }

    // 递减扫描
    while (i + 1 < arrSize && arr[i] > arr[i + 1]) {
        i++;
    }

    return i == arrSize - 1;
}

复杂度分析

• 时间复杂度：O(N)，其中 N 是数组 arr 的长度。

• 空间复杂度：O(1)。