0951-翻转等价二叉树

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:30 2023-09-13 16:06:30 Updated    

我们可以为二叉树 T 定义一个 **翻转操作 **，如下所示：选择任意节点，然后交换它的左子树和右子树。

只要经过一定次数的翻转操作后，能使 X 等于 Y ，我们就称二叉树 X _翻转 等价 _于二叉树 Y 。

这些树由根节点 root1 和 root2 给出。如果两个二叉树是否是 _翻转 等价 _的函数，则返回 true ，否则返回 false
。

示例 1：

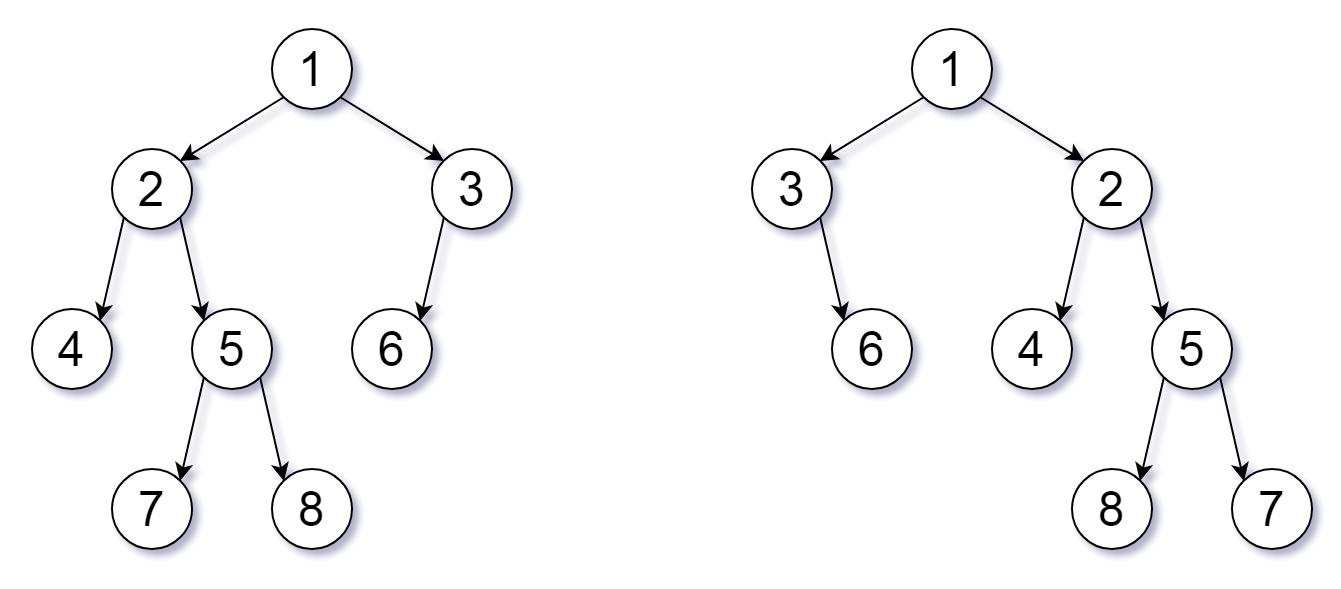
Flipped Trees Diagram

**输入：** root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
**输出：** true
**解释：** 我们翻转值为 1，3 以及 5 的三个节点。

示例 2:

**输入:** root1 = [], root2 = []
**输出:** true

示例 3:

**输入:** root1 = [], root2 = [1]
**输出:** false

提示：

  • 每棵树节点数在 [0, 100] 范围内
  • 每棵树中的每个值都是唯一的、在 [0, 99] 范围内的整数

方法一： 递归

思路

如果二叉树 root1，root2 根节点值相等，那么只需要检查他们的孩子是不是相等就可以了。

算法

存在三种情况：

  • 如果 root1 或者 root2 是 null，那么只有在他们都为 null 的情况下这两个二叉树才等价。
  • 如果 root1，root2 的值不相等，那这两个二叉树的一定不等价。
  • 如果以上条件都不满足，也就是当 root1 和 root2 的值相等的情况下，需要继续判断 root1 的孩子节点是不是跟 root2 的孩子节点相当。因为可以做翻转操作，所以这里有两种情况需要去判断。
[solution1-Java]
1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public boolean flipEquiv(TreeNode root1, TreeNode root2) {
        if (root1 == root2)
            return true;
        if (root1 == null || root2 == null || root1.val != root2.val)
            return false;

        return (flipEquiv(root1.left, root2.left) && flipEquiv(root1.right, root2.right) ||
                flipEquiv(root1.left, root2.right) && flipEquiv(root1.right, root2.left));
    }
}
[solution1-Python]
1
2
3
4
5
6
7
8
9
10
11
class Solution(object):
    def flipEquiv(self, root1, root2):
        if root1 is root2:
            return True
        if not root1 or not root2 or root1.val != root2.val:
            return False

        return (self.flipEquiv(root1.left, root2.left) and
                self.flipEquiv(root1.right, root2.right) or
                self.flipEquiv(root1.left, root2.right) and
                self.flipEquiv(root1.right, root2.left))

复杂度分析

  • 时间复杂度： O(min(N_1, N_2))，其中 N_1，N_2 分别是二叉树 root1，root2 的大小。

  • 空间复杂度： O(min(H_1, H_2))，其中 H_1，H_2 分别是二叉树 root1， root2 的高度。

方法二： 标准态遍历

思路

让树中所有节点的左孩子都小于右孩子，如果当前不满足就翻转。我们把这种状态的二叉树称为 标准态。所有等价二叉树在转换成标准态后都是完全一样的。

算法

用深度优先遍历来对比这两棵树在标准态下是否完全一致。对于两颗等价树，在标准态下遍历的结果一定是一样的。

[solution2-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public boolean flipEquiv(TreeNode root1, TreeNode root2) {
        List<Integer> vals1 = new ArrayList();
        List<Integer> vals2 = new ArrayList();
        dfs(root1, vals1);
        dfs(root2, vals2);
        return vals1.equals(vals2);
    }

    public void dfs(TreeNode node, List<Integer> vals) {
        if (node != null) {
            vals.add(node.val);
            int L = node.left != null ? node.left.val : -1;
            int R = node.right != null ? node.right.val : -1;

            if (L < R) {
                dfs(node.left, vals);
                dfs(node.right, vals);
            } else {
                dfs(node.right, vals);
                dfs(node.left, vals);
            }

            vals.add(null);
        }
    }
}

[solution2-Python]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution:
    def flipEquiv(self, root1, root2):
        def dfs(node):
            if node:
                yield node.val
                L = node.left.val if node.left else -1
                R = node.right.val if node.right else -1
                if L < R:
                    yield from dfs(node.left)
                    yield from dfs(node.right)
                else:
                    yield from dfs(node.right)
                    yield from dfs(node.left)
                yield '#'

        return all(x == y for x, y in itertools.zip_longest(
            dfs(root1), dfs(root2)))

复杂度分析

  • 时间复杂度： O(N_1 + N_2)，其中 N_1，N_2 分别为二叉树 root1，root2 的大小（在 Python 实现中，复杂度为 O(\min(N_1, N_2))。）

  • 空间复杂度： O(N_1 + N_2)。其中 H_1，H_2 是二叉树 root1，root2 的高度。（在 Python 实现中，复杂度为 O(\min(H_1, H_2))。）

 Comments
On this page
0951-翻转等价二叉树