0958-二叉树的完全性检验

给你一棵二叉树的根节点 root ，请你判断这棵树是否是一棵 完全二叉树 。

在一棵 完全二叉树
中，除了最后一层外，所有层都被完全填满，并且最后一层中的所有节点都尽可能靠左。最后一层（第 h 层）中可以包含 1 到 2h 个节点。

示例 1：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/15/complete-binary-tree-1.png)

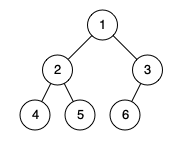
**输入：** root = [1,2,3,4,5,6]
**输出：** true
**解释：** 最后一层前的每一层都是满的（即，节点值为 {1} 和 {2,3} 的两层），且最后一层中的所有节点（{4,5,6}）尽可能靠左。

示例 2：

![](https://assets.leetcode-cn.com/aliyun-lc-
upload/uploads/2018/12/15/complete-binary-tree-2.png)

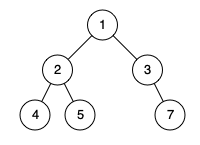
**输入：** root = [1,2,3,4,5,null,7]
**输出：** false
**解释：** 值为 7 的节点不满足条件「节点尽可能靠左」。

提示：

• 树中节点数目在范围 [1, 100] 内
• 1 <= Node.val <= 1000

方法 1：广度优先搜索

想法

这个问题可以简化成两个小问题：用 (depth, position) 元组表示每个节点的”位置“；确定如何定义所有节点都是在最左边的。

假如我们在深度为 3 的行有 4 个节点，位置为 0，1，2，3；那么就有 8 个深度为 4 的新节点位置在 0，1，2，3，4，5，6，7；所以我们可以找到规律：对于一个节点，它的左孩子为：(depth, position) -> (depth + 1, position * 2)，右孩子为 (depth, position) -> (depth + 1, position * 2 + 1)。所以，对于深度为 d 的行恰好含有 2^{d-1 个节点，所有节点都是靠左边排列的当他们的位置编号是 0, 1, ... 且没有间隙。

一个更简单的表示深度和位置的方法是：用 1 表示根节点，对于任意一个节点 v，它的左孩子为 2*v 右孩子为 2*v + 1。这就是我们用的规则，在这个规则下，一颗二叉树是完全二叉树当且仅当节点编号依次为 1, 2, 3, ... 且没有间隙。

算法

对于根节点，我们定义其编号为 1。然后，对于每个节点 v，我们将其左节点编号为 2 * v，将其右节点编号为 2 * v + 1。

我们可以发现，树中所有节点的编号按照广度优先搜索顺序正好是升序。（也可以使用深度优先搜索，之后对序列排序）。

然后，我们检测编号序列是否为无间隔的 1, 2, 3, …，事实上，我们只需要检查最后一个编号是否正确，因为最后一个编号的值最大。

[]

class Solution {
    public boolean isCompleteTree(TreeNode root) {
        List<ANode> nodes = new ArrayList();
        nodes.add(new ANode(root, 1));
        int i = 0;
        while (i < nodes.size()) {
            ANode anode = nodes.get(i++);
            if (anode.node != null) {
                nodes.add(new ANode(anode.node.left, anode.code * 2));
                nodes.add(new ANode(anode.node.right, anode.code * 2 + 1));
            }
        }

        return nodes.get(i-1).code == nodes.size();
    }
}

class ANode {  // Annotated Node
    TreeNode node;
    int code;
    ANode(TreeNode node, int code) {
        this.node = node;
        this.code = code;
    }
}

[]

class Solution(object):
    def isCompleteTree(self, root):
        nodes = [(root, 1)]
        i = 0
        while i < len(nodes):
            node, v = nodes[i]
            i += 1
            if node:
                nodes.append((node.left, 2*v))
                nodes.append((node.right, 2*v+1))

        return  nodes[-1][1] == len(nodes)

复杂度分析

• 时间复杂度：O(N)，其中 N 是树节点个数。
• 空间复杂度：O(N)。