0971-翻转二叉树以匹配先序遍历

给你一棵二叉树的根节点 root ，树中有 n 个节点，每个节点都有一个不同于其他节点且处于 1 到 n 之间的值。

另给你一个由 n 个值组成的行程序列 voyage ，表示 预期 的二叉树
先序遍历
结果。

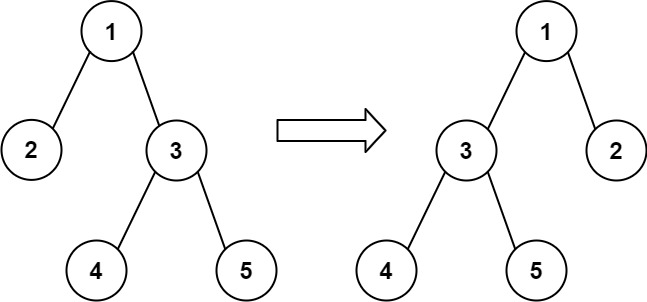
通过交换节点的左右子树，可以 翻转 该二叉树中的任意节点。例，翻转节点 1 的效果如下：

请翻转 最少 的树中节点，使二叉树的 先序遍历 与预期的遍历行程 voyage 相匹配 。

如果可以，则返回 翻转的 所有节点的值的列表。你可以按任何顺序返回答案。如果不能，则返回列表 [-1]。

示例 1：

**输入：** root = [1,2], voyage = [2,1]
**输出：** [-1]
**解释：** 翻转节点无法令先序遍历匹配预期行程。

示例 2：

**输入：** root = [1,2,3], voyage = [1,3,2]
**输出：** [1]
**解释：** 交换节点 2 和 3 来翻转节点 1 ，先序遍历可以匹配预期行程。

示例 3：

**输入：** root = [1,2,3], voyage = [1,2,3]
**输出：** []
**解释：** 先序遍历已经匹配预期行程，所以不需要翻转节点。

提示：

• 树中的节点数目为 n
• n == voyage.length
• 1 <= n <= 100
• 1 <= Node.val, voyage[i] <= n
• 树中的所有值 互不相同
• voyage 中的所有值 互不相同

方法：深度优先搜索

思路

当做先序遍历的时候，我们可能会翻转某一个节点，尝试使我们当前的遍历序列与给定的行程序列相匹配。

如果我们希望先序遍历序列的下一个数字是 voyage[i] ，那么至多只有一种可行的遍历路径供我们选择，因为所有节点的值都不相同。

算法

进行深度优先遍历。如果遍历到某一个节点的时候，节点值不能与行程序列匹配，那么答案一定是 [-1]。

否则，当行程序列中的下一个期望数字 voyage[i] 与我们即将遍历的子节点的值不同的时候，我们就要翻转一下当前这个节点。

[Qqi74tmF-Java]

class Solution {
    List<Integer> flipped;
    int index;
    int[] voyage;

    public List<Integer> flipMatchVoyage(TreeNode root, int[] voyage) {
        flipped = new ArrayList();
        index = 0;
        this.voyage = voyage;

        dfs(root);
        if (!flipped.isEmpty() && flipped.get(0) == -1) {
            flipped.clear();
            flipped.add(-1);
        }

        return flipped;
    }

    public void dfs(TreeNode node) {
        if (node != null) {
            if (node.val != voyage[index++]) {
                flipped.clear();
                flipped.add(-1);
                return;
            }

            if (index < voyage.length && node.left != null &&
                    node.left.val != voyage[index]) {
                flipped.add(node.val);
                dfs(node.right);
                dfs(node.left);
            } else {
                dfs(node.left);
                dfs(node.right);
            }
        }
    }
}

[Qqi74tmF-Python]

class Solution(object):
    def flipMatchVoyage(self, root, voyage):
        self.flipped = []
        self.i = 0

        def dfs(node):
            if node:
                if node.val != voyage[self.i]:
                    self.flipped = [-1]
                    return
                self.i += 1

                if (self.i < len(voyage) and
                        node.left and node.left.val != voyage[self.i]):
                    self.flipped.append(node.val)
                    dfs(node.right)
                    dfs(node.left)
                else:
                    dfs(node.left)
                    dfs(node.right)

        dfs(root)
        if self.flipped and self.flipped[0] == -1:
            self.flipped = [-1]
        return self.flipped

复杂度分析

• 时间复杂度：O(N)，其中 N 是给定树中节点的数量。

• 空间复杂度：O(N)。