0986-区间列表的交集
给定两个由一些 闭区间 组成的列表,firstList 和 secondList ,其中 firstList[i] = [starti, endi] 而 secondList[j] = [startj, endj] 。每个区间列表都是成对 不相交 的,并且 已经排序 。
返回这 两个区间列表的交集 。
形式上, 闭区间 [a, b](其中 a <= b)表示实数 x 的集合,而 a <= x <= b 。
两个闭区间的 交集 是一组实数,要么为空集,要么为闭区间。例如,[1, 3] 和 [2, 4] 的交集为 [2, 3] 。
示例 1:
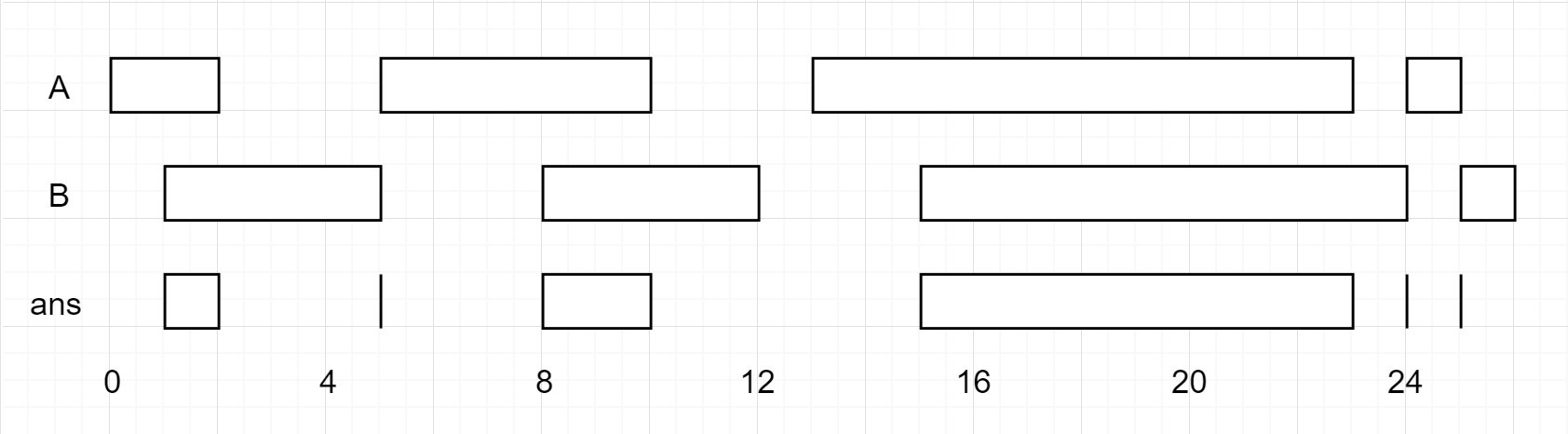
**输入:** firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
**输出:** [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]
示例 2:
**输入:** firstList = [[1,3],[5,9]], secondList = []
**输出:** []
示例 3:
**输入:** firstList = [], secondList = [[4,8],[10,12]]
**输出:** []
示例 4:
**输入:** firstList = [[1,7]], secondList = [[3,10]]
**输出:** [[3,7]]
提示:
0 <= firstList.length, secondList.length <= 1000firstList.length + secondList.length >= 10 <= starti < endi <= 109endi < starti+10 <= startj < endj <= 109endj < startj+1
方法:归并区间
思路
我们称 b 为区间 [a, b] 的末端点。
在两个数组给定的所有区间中,假设拥有最小末端点的区间是 A[0]。(为了不失一般性,该区间出现在数组 A 中)
然后,在数组 B 的区间中, A[0] 只可能与数组 B 中的至多一个区间相交。(如果 B 中存在两个区间均与 A[0] 相交,那么它们将共同包含 A[0] 的末端点,但是 B 中的区间应该是不相交的,所以存在矛盾)
算法
如果 A[0] 拥有最小的末端点,那么它只可能与 B[0] 相交。然后我们就可以删除区间 A[0],因为它不能与其他任何区间再相交了。
相似的,如果 B[0] 拥有最小的末端点,那么它只可能与区间 A[0] 相交,然后我们就可以将 B[0] 删除,因为它无法再与其他区间相交了。
我们用两个指针 i 与 j 来模拟完成删除 A[0] 或 B[0] 的操作。
1 | class Solution { |
1 | class Solution: |
复杂度分析
时间复杂度:O(M + N),其中 M, N 分别是数组
A和B的长度。空间复杂度:O(M + N),答案中区间数量的上限。
Comments