给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b"
或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。
只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。
示例 1：
**输入：** ["a==b","b!=a"]
**输出：** false
**解释：** 如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。
示例 2：
**输入：** ["b==a","a==b"]
**输出：** true
**解释：** 我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。
示例 3：
**输入：** ["a==b","b==c","a==c"]
**输出：** true
示例 4：
**输入：** ["a==b","b!=c","c==a"]
**输出：** false
示例 5：
**输入：** ["c==c","b==d","x!=z"]
**输出：** true
提示：
1 <= equations.length <= 500equations[i].length == 4equations[i][0] 和 equations[i][3] 是小写字母equations[i][1] 要么是 '='，要么是 '!'equations[i][2] 是 '='
📺 视频题解
📖 文字题解
方法一：并查集
我们可以将每一个变量看作图中的一个节点，把相等的关系 == 看作是连接两个节点的边，那么由于表示相等关系的等式方程具有传递性，即如果 a==b 和 b==c 成立，则 a==c 也成立。也就是说，所有相等的变量属于同一个连通分量。因此，我们可以使用并查集来维护这种连通分量的关系。
首先遍历所有的等式，构造并查集。同一个等式中的两个变量属于同一个连通分量，因此将两个变量进行合并。
然后遍历所有的不等式。同一个不等式中的两个变量不能属于同一个连通分量，因此对两个变量分别查找其所在的连通分量，如果两个变量在同一个连通分量中，则产生矛盾，返回 false。
如果遍历完所有的不等式没有发现矛盾，则返回 true。
{:width=”90%”}
具体实现方面，使用一个数组 parent 存储每个变量的连通分量信息，其中的每个元素表示当前变量所在的连通分量的父节点信息，如果父节点是自身，说明该变量为所在的连通分量的根节点。一开始所有变量的父节点都是它们自身。对于合并操作，我们将第一个变量的根节点的父节点指向第二个变量的根节点；对于查找操作，我们沿着当前变量的父节点一路向上查找，直到找到根节点。
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
| class Solution {
public boolean equationsPossible(String[] equations) {
int[] parent = new int[26];
for (int i = 0; i < 26; i++) {
parent[i] = i;
}
for (String str : equations) {
if (str.charAt(1) == '=') {
int index1 = str.charAt(0) - 'a';
int index2 = str.charAt(3) - 'a';
union(parent, index1, index2);
}
}
for (String str : equations) {
if (str.charAt(1) == '!') {
int index1 = str.charAt(0) - 'a';
int index2 = str.charAt(3) - 'a';
if (find(parent, index1) == find(parent, index2)) {
return false;
}
}
}
return true;
}
public void union(int[] parent, int index1, int index2) {
parent[find(parent, index1)] = find(parent, index2);
}
public int find(int[] parent, int index) {
while (parent[index] != index) {
parent[index] = parent[parent[index]];
index = parent[index];
}
return index;
}
}
|
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| class UnionFind {
private:
vector<int> parent;
public:
UnionFind() {
parent.resize(26);
iota(parent.begin(), parent.end(), 0);
}
int find(int index) {
if (index == parent[index]) {
return index;
}
parent[index] = find(parent[index]);
return parent[index];
}
void unite(int index1, int index2) {
parent[find(index1)] = find(index2);
}
};
class Solution {
public:
bool equationsPossible(vector<string>& equations) {
UnionFind uf;
for (const string& str: equations) {
if (str[1] == '=') {
int index1 = str[0] - 'a';
int index2 = str[3] - 'a';
uf.unite(index1, index2);
}
}
for (const string& str: equations) {
if (str[1] == '!') {
int index1 = str[0] - 'a';
int index2 = str[3] - 'a';
if (uf.find(index1) == uf.find(index2)) {
return false;
}
}
}
return true;
}
};
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution:
class UnionFind:
def __init__(self):
self.parent = list(range(26))
def find(self, index):
if index == self.parent[index]:
return index
self.parent[index] = self.find(self.parent[index])
return self.parent[index]
def union(self, index1, index2):
self.parent[self.find(index1)] = self.find(index2)
def equationsPossible(self, equations: List[str]) -> bool:
uf = Solution.UnionFind()
for st in equations:
if st[1] == "=":
index1 = ord(st[0]) - ord("a")
index2 = ord(st[3]) - ord("a")
uf.union(index1, index2)
for st in equations:
if st[1] == "!":
index1 = ord(st[0]) - ord("a")
index2 = ord(st[3]) - ord("a")
if uf.find(index1) == uf.find(index2):
return False
return True
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| func equationsPossible(equations []string) bool {
parent := make([]int, 26)
for i := 0; i < 26; i++ {
parent[i] = i
}
for _, str := range equations {
if str[1] == '=' {
index1 := int(str[0] - 'a')
index2 := int(str[3] - 'a')
union(parent, index1, index2)
}
}
for _, str := range equations {
if str[1] == '!' {
index1 := int(str[0] - 'a')
index2 := int(str[3] - 'a')
if find(parent, index1) == find(parent, index2) {
return false
}
}
}
return true
}
func union(parent []int, index1, index2 int) {
parent[find(parent, index1)] = find(parent, index2)
}
func find(parent []int, index int) int {
for parent[index] != index {
parent[index] = parent[parent[index]]
index = parent[index]
}
return index
}
|
复杂度分析
时间复杂度：O(n+C \log C)，其中 n 是 equations 中的方程数量，C 是变量的总数，在本题中变量都是小写字母，即 C \leq 26。上面的并查集代码中使用了路径压缩优化，对于每个方程的合并和查找的均摊时间复杂度都是 O(\log C)。由于需要遍历每个方程，因此总时间复杂度是 O(n+C \log C)。
空间复杂度：O(C)。创建一个数组 parent 存储每个变量的连通分量信息，由于变量都是小写字母，因此 parent 是长度为 C。
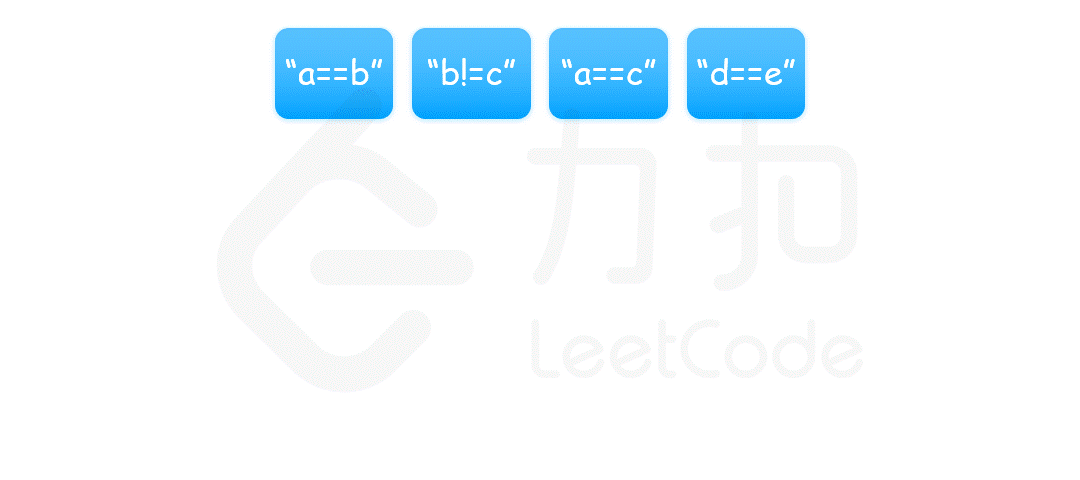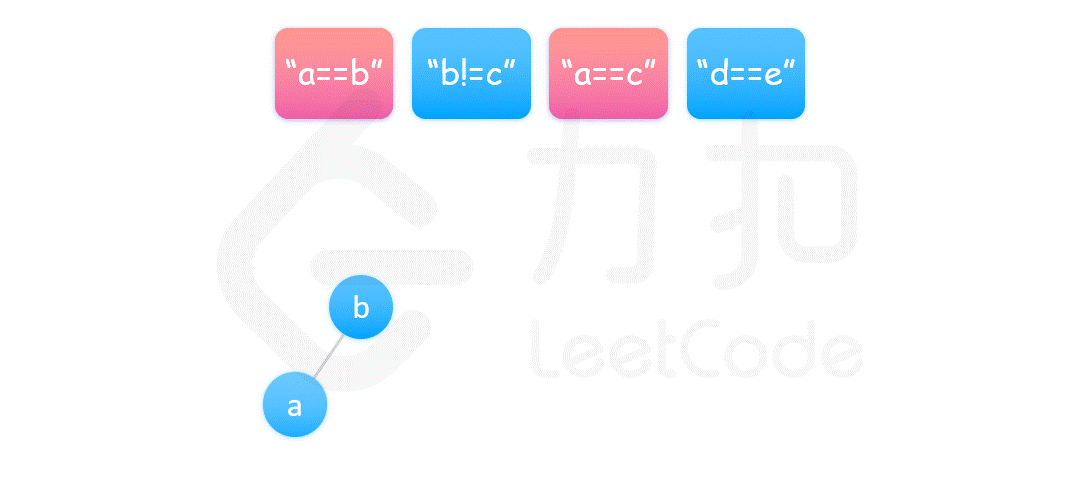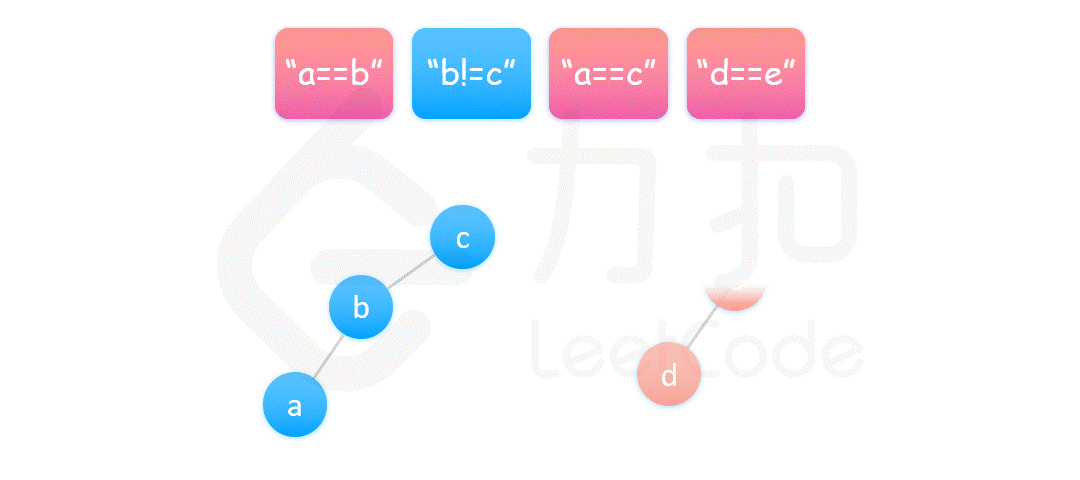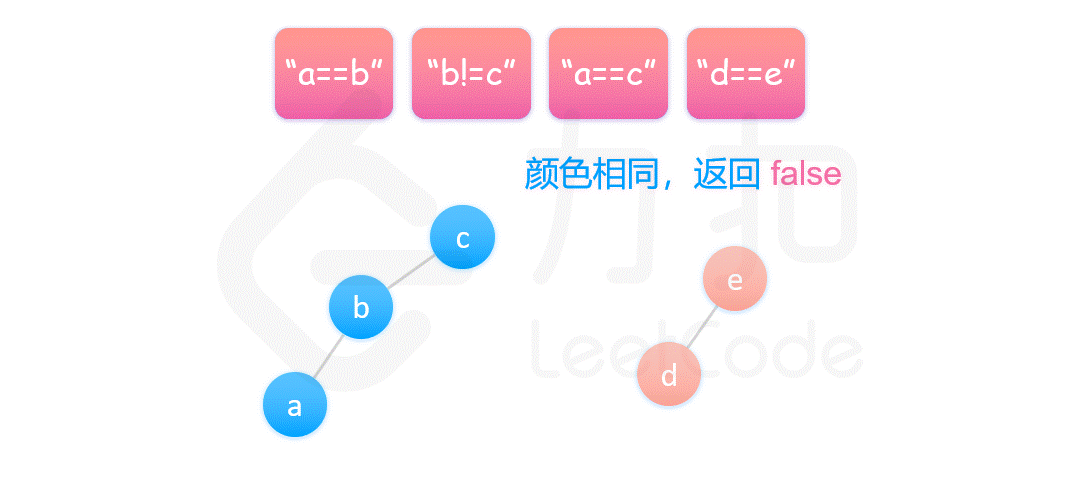{:width=”90%”}