0992-K 个不同整数的子数组

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:26 2023-09-13 16:06:26 Updated    

给定一个正整数数组 nums和一个整数 k，返回 nums 中 「 好子数组」 _ _ 的数目。

如果 nums 的某个子数组中不同整数的个数恰好为 k，则称 nums 的这个连续、不一定不同的子数组为 「 好子数组 」 。

  • 例如，[1,2,3,1,2] 中有 3 个不同的整数：1，2，以及 3。

子数组 是数组的 连续 部分。

示例 1：

**输入：** nums = [1,2,1,2,3], k = 2
**输出：** 7
**解释：** 恰好由 2 个不同整数组成的子数组：[1,2], [2,1], [1,2], [2,3], [1,2,1], [2,1,2], [1,2,1,2].

示例 2：

**输入：** nums = [1,2,1,3,4], k = 3
**输出：** 3
**解释：** 恰好由 3 个不同整数组成的子数组：[1,2,1,3], [2,1,3], [1,3,4].

提示：

  • 1 <= nums.length <= 2 * 104
  • 1 <= nums[i], k <= nums.length

📺 视频讲解

力扣君温馨小贴士：觉得视频时间长的扣友，可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看。

992. K 个不同整数的子数组.mp4

最初直觉使用双指针算法遇到的问题

对于一个固定的左边界来说，满足「恰好存在 K 个不同整数的子区间」的右边界 不唯一，且形成区间。

示例 1：左边界固定的时候，恰好存在 2 个不同整数的子区间为 [1,2],[1,2,1],[1,2,1,2] ，总数为 3。其值为下标 3 - 1 + 1，即区间 [1..3] 的长度。

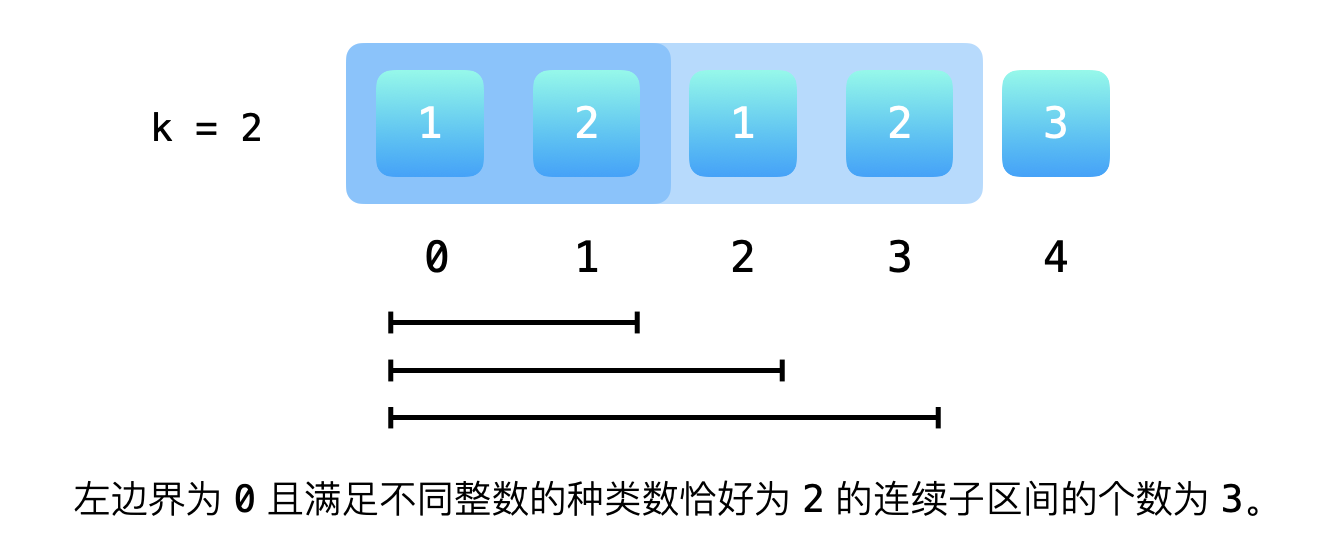image.png{:width=500}

须要找到左边界固定的情况下，满足「恰好存在 K 个不同整数的子区间」最小右边界和最大右边界。对比以前我们做过的，使用双指针解决的问题的问法基本都会出现「最小」、「最大」这样的字眼。

把原问题转换成为容易求解的问题

友情提示：这里把 「恰好」 转换成为 「最多」须要一点求解「双指针（滑动窗口）」问题的经验。建立在熟练掌握这一类问题求解思路的基础上。

把「恰好」改成「最多」就可以使用双指针一前一后交替向右的方法完成，这是因为 对于每一个确定的左边界，最多包含 K 种不同整数的右边界是唯一确定的，并且在左边界向右移动的过程中，右边界或者在原来的地方，或者在原来地方的右边。

而「最多存在 K 个不同整数的子区间的个数」与「恰好存在 K 个不同整数的子区间的个数」的差恰好等于「最多存在 K - 1 个不同整数的子区间的个数」。

image.png

因为原问题就转换成为求解「最多存在 K 个不同整数的子区间的个数」与 「最多存在 K - 1 个不同整数的子区间的个数」，它们其实是一个问题。

方法：双指针（滑动窗口）

实现函数 atMostWithKDistinct(A, K) ，表示「最多存在 K 个不同整数的子区间的个数」。于是 atMostWithKDistinct(A, K) - atMostWithKDistinct(A, K - 1) 即为所求。

参考代码：

[]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class Solution {

    public int subarraysWithKDistinct(int[] A, int K) {
        return atMostKDistinct(A, K) - atMostKDistinct(A, K - 1);
    }

    /**
     * @param A
     * @param K
     * @return 最多包含 K 个不同整数的子区间的个数
     */
    private int atMostKDistinct(int[] A, int K) {
        int len = A.length;
        int[] freq = new int[len + 1];

        int left = 0;
        int right = 0;
        // [left, right) 里不同整数的个数
        int count = 0;
        int res = 0;
        // [left, right) 包含不同整数的个数小于等于 K
        while (right < len) {
            if (freq[A[right]] == 0) {
                count++;
            }
            freq[A[right]]++;
            right++;

            while (count > K) {
                freq[A[left]]--;
                if (freq[A[left]] == 0) {
                    count--;
                }
                left++;
            }
            // [left, right) 区间的长度就是对结果的贡献
            res += right - left;
        }
        return res;
    }
}

说明： res += right - left; 这行代码的意思：

用具体的例子理解：最多包含 3 种不同整数的子区间 [1, 3, 2, 3] （双指针算法是在左边界固定的前提下，让右边界走到最右边），当前可以确定 1 开始的满足最多包含 3 种不同整数的子区间有 [1]、[1, 3]、[1, 3, 2]、[1, 3, 2, 3]。

所有的 左边界固定前提下，根据右边界最右的下标，计算出来的子区间的个数就是整个函数要返回的值。用右边界固定的前提下，左边界最左边的下标去计算也是完全可以的。

复杂度分析：

  • 时间复杂度：O(N)，这里 N 是输入数组的长度；
  • 空间复杂度：O(N)，使用了常数个变量、频数数组的长度为 N + 1。

总结

使用双指针（滑动窗口、两个变量一前一后交替向后移动）解决的问题通常都和这个问题要问的结果有关。以我们在题解中给出的 5 道经典问题为例：

  • 3. 无重复字符的最长子串：没有重复的子串，一定只会问「最长」，因为最短的没有重复字符的子串是只有一个字符的子串；
  • 76. 最小覆盖子串：求一个字符串的子串覆盖另一个字符串的长度一定是问「最小」，而不会问「最大」，因为最大一定是整个字符串；
  • 209. 长度最小的子数组：所有元素都是正整数，且子区间里所有元素的和大于等于定值 s 的子区间一定是问长度「最小」，而不会问「最多」，因为最多也一定是整个数组的长度；
  • 159. 至多包含两个不同字符的最长子串：最多包含两个不同字符一定是问「最长」才有意义，因为长度更长的子串可能会包含更多的字符；
  • 424. 替换后的最长重复字符：替换的次数 k 是定值，替换以后字符全部相等的子串也一定只会问「最长」。

练习

提示：在做这些问题的时候，一定要思考清楚为什么可以采用双指针（滑动窗口）算法解决如上的问题，为什么 左、右指针向右移动的时候可以不回头。如果不太熟悉这一类问题思路的朋友，一定要想清楚算法为什么有效，比知道这些问题可以用双指针（滑动窗口）算法解决重要得多。

思路一般是这样：固定左边界的前提下，如果较短的区间性质是什么样的，较长的区间的性质其实我们也可以推测出来。在右边界固定的前提下，我们须要将左边界右移，如此反复。这样的算法只遍历了数组两次，不用枚举所有可能的区间，把 O(N^2) 的时间复杂度降到了 O(N)。

 Comments
On this page
0992-K 个不同整数的子数组
  1. 📺 视频讲解
  2. 方法：双指针（滑动窗口）
  3. 总结
  4. 练习