最大树 定义:一棵树,并满足:其中每个节点的值都大于其子树中的任何其他值。
给你最大树的根节点 root 和一个整数 val 。
就像 之前的问题 那样,给定的树是利用
Construct(a) 例程从列表 a(root = Construct(a))递归地构建的:
- 如果
a 为空,返回 null 。
- 否则,令
a[i] 作为 a 的最大元素。创建一个值为 a[i] 的根节点 root 。
root 的左子树将被构建为 Construct([a[0], a[1], ..., a[i - 1]]) 。root 的右子树将被构建为 Construct([a[i + 1], a[i + 2], ..., a[a.length - 1]]) 。- 返回
root 。
请注意,题目没有直接给出 a ,只是给出一个根节点 root = Construct(a) 。
假设 b 是 a 的副本,并在末尾附加值 val。题目数据保证 b 中的值互不相同。
返回 Construct(b) 。
示例 1:
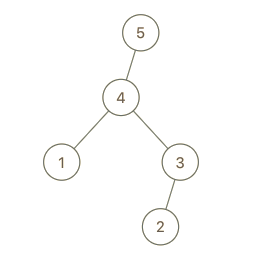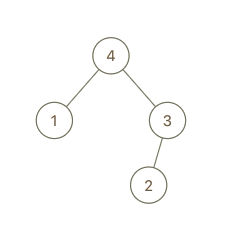
**输入:** root = [4,1,3,null,null,2], val = 5
**输出:** [5,4,null,1,3,null,null,2]
**解释:** a = [1,4,2,3], b = [1,4,2,3,5]
示例 2:
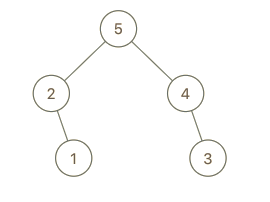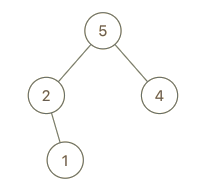
**输入:** root = [5,2,4,null,1], val = 3
**输出:** [5,2,4,null,1,null,3]
**解释:** a = [2,1,5,4], b = [2,1,5,4,3]
示例 3:
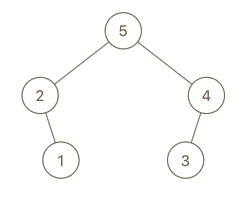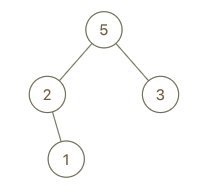
**输入:** root = [5,2,3,null,1], val = 4
**输出:** [5,2,4,null,1,3]
**解释:** a = [2,1,5,3], b = [2,1,5,3,4]
提示:
- 树中节点数目在范围
[1, 100] 内
1 <= Node.val <= 100- 树中的所有值 互不相同
1 <= val <= 100
方法一:遍历右子节点
思路与算法
如果根节点的值小于给定的整数 val,那么新的树会以 val 作为根节点,并将原来的树作为新的根节点的左子树。
否则,我们从根节点开始不断地向右子节点进行遍历。这是因为,当遍历到的节点的值大于 val 时,由于 val 是新添加的位于数组末尾的元素,那么在构造的结果中,val 一定出现在该节点的右子树中。
当我们遍历到节点 cur 以及它的父节点 parent,并且 cur 节点的值小于 val 时,我们就可以停止遍历,构造一个新的节点,以 val 为值且以 cur 为左子树。我们将该节点作为 parent 的新的右节点,并返回根节点作为答案即可。
如果遍历完成之后,仍然没有找到比 val 值小的节点,那么我们构造一个新的节点,以 val 为值,将该节点作为 parent 的右节点,并返回根节点作为答案即可。
代码
[sol1-C++]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| class Solution {
public:
TreeNode* insertIntoMaxTree(TreeNode* root, int val) {
TreeNode* parent = nullptr;
TreeNode* cur = root;
while (cur) {
if (val > cur->val) {
if (!parent) {
return new TreeNode(val, root, nullptr);
}
TreeNode* node = new TreeNode(val, cur, nullptr);
parent->right = node;
return root;
}
else {
parent = cur;
cur = cur->right;
}
}
parent->right = new TreeNode(val);
return root;
}
};
|
[sol1-Java]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public TreeNode insertIntoMaxTree(TreeNode root, int val) {
TreeNode parent = null;
TreeNode cur = root;
while (cur != null) {
if (val > cur.val) {
if (parent == null) {
return new TreeNode(val, root, null);
}
TreeNode node = new TreeNode(val, cur, null);
parent.right = node;
return root;
} else {
parent = cur;
cur = cur.right;
}
}
parent.right = new TreeNode(val);
return root;
}
}
|
[sol1-C#]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| public class Solution {
public TreeNode InsertIntoMaxTree(TreeNode root, int val) {
TreeNode parent = null;
TreeNode cur = root;
while (cur != null) {
if (val > cur.val) {
if (parent == null) {
return new TreeNode(val, root, null);
}
TreeNode node = new TreeNode(val, cur, null);
parent.right = node;
return root;
} else {
parent = cur;
cur = cur.right;
}
}
parent.right = new TreeNode(val);
return root;
}
}
|
[sol1-Python3]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| class Solution:
def insertIntoMaxTree(self, root: Optional[TreeNode], val: int) -> Optional[TreeNode]:
parent, cur = None, root
while cur:
if val > cur.val:
if not parent:
return TreeNode(val, root, None)
node = TreeNode(val, cur, None)
parent.right = node
return root
else:
parent = cur
cur = cur.right
parent.right = TreeNode(val)
return root
|
[sol1-C]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| struct TreeNode* creatTreeNode(int val, const struct TreeNode *left, const struct TreeNode *right) {
struct TreeNode* node = (struct TreeNode *)malloc(sizeof(struct TreeNode));
node->val = val;
node->left = left;
node->right = right;
return node;
}
struct TreeNode* insertIntoMaxTree(struct TreeNode* root, int val){
struct TreeNode* parent = NULL;
struct TreeNode* cur = root;
struct TreeNode* node = NULL;
while (cur) {
if (val > cur->val) {
if (!parent) {
return creatTreeNode(val, root, NULL);
}
parent->right = creatTreeNode(val, cur, NULL);
return root;
}
else {
parent = cur;
cur = cur->right;
}
}
parent->right = creatTreeNode(val, NULL, NULL);;
return root;
}
|
[sol1-Golang]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| func insertIntoMaxTree(root *TreeNode, val int) *TreeNode {
var parent *TreeNode
for cur := root; cur != nil; cur = cur.Right {
if val > cur.Val {
if parent == nil {
return &TreeNode{val, root, nil}
}
parent.Right = &TreeNode{val, cur, nil}
return root
}
parent = cur
}
parent.Right = &TreeNode{Val: val}
return root
}
|
[sol1-JavaScript]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
| var insertIntoMaxTree = function(root, val) {
let parent = null;
let cur = root;
while (cur) {
if (val > cur.val) {
if (!parent) {
return new TreeNode(val, root, null);
}
let node = new TreeNode(val, cur, null);
parent.right = node;
return root;
} else {
parent = cur;
cur = cur.right;
}
}
parent.right = new TreeNode(val);
return root;
};
|
复杂度分析