1001-网格照明

Raphael Liu Lv10
  2023-09-13 00:47:26 2023-09-13 00:47:26 Created   2023-09-13 16:06:25 2023-09-13 16:06:25 Updated    

在大小为 n x n 的网格 grid 上，每个单元格都有一盏灯，最初灯都处于 关闭 状态。

给你一个由灯的位置组成的二维数组 lamps ，其中 lamps[i] = [rowi, coli] 表示 打开 位于
grid[rowi][coli] 的灯。即便同一盏灯可能在 lamps 中多次列出，不会影响这盏灯处于 打开 状态。

当一盏灯处于打开状态，它将会照亮 自身所在单元格 以及同一 行 、同一 列 和两条 对角线 上的 所有其他单元格 。

另给你一个二维数组 queries ，其中 queries[j] = [rowj, colj] 。对于第 j 个查询，如果单元格 [rowj, colj] 是被照亮的，则查询结果为 1 ，否则为 0 。在第 j 次查询之后 [按照查询的顺序] ， 关闭 位于单元格
grid[rowj][colj] 上及相邻 8 个方向上（与单元格 grid[rowi][coli] 共享角或边）的任何灯。

返回一个整数数组 ans 作为答案， ans[j] 应等于第 j 次查询 queries[j] 的结果，1 表示照亮，0
表示未照亮。

示例 1：

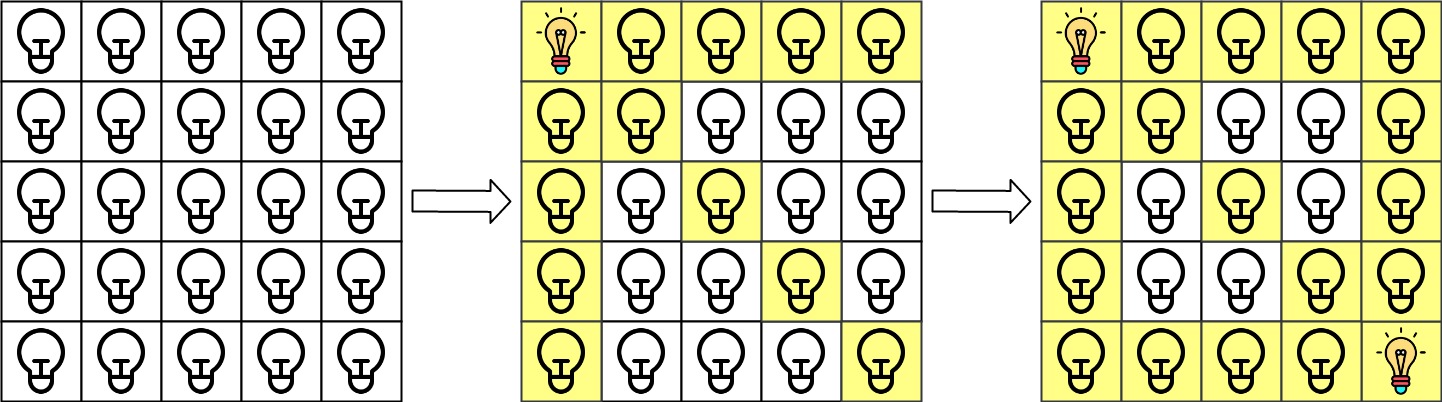
**输入：** n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,0]]
**输出：** [1,0]
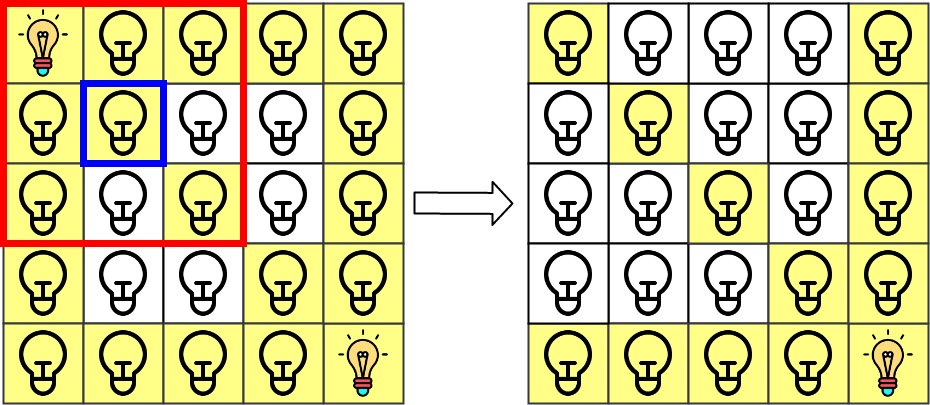
**解释：** 最初所有灯都是关闭的。在执行查询之前，打开位于 [0, 0] 和 [4, 4] 的灯。第 0 次查询检查 grid[1][1] 是否被照亮（蓝色方框）。该单元格被照亮，所以 ans[0] = 1 。然后，关闭红色方框中的所有灯。
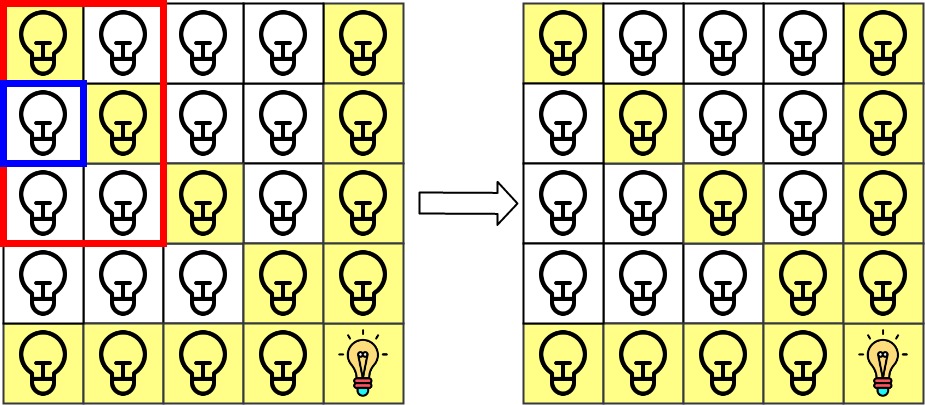
![](https://assets.leetcode.com/uploads/2020/08/19/illu_step1.jpg)
第 1 次查询检查 grid[1][0] 是否被照亮（蓝色方框）。该单元格没有被照亮，所以 ans[1] = 0 。然后，关闭红色矩形中的所有灯。
![](https://assets.leetcode.com/uploads/2020/08/19/illu_step2.jpg)

示例 2：

**输入：** n = 5, lamps = [[0,0],[4,4]], queries = [[1,1],[1,1]]
**输出：** [1,1]

示例 3：

**输入：** n = 5, lamps = [[0,0],[0,4]], queries = [[0,4],[0,1],[1,4]]
**输出：** [1,1,0]

提示：

  • 1 <= n <= 109
  • 0 <= lamps.length <= 20000
  • 0 <= queries.length <= 20000
  • lamps[i].length == 2
  • 0 <= rowi, coli < n
  • queries[j].length == 2
  • 0 <= rowj, colj < n

方法一：哈希表

思路与算法

将网格转换成一个坐标系，行下标作为 x 坐标，列下标作为 y 坐标。我们使用直线与坐标轴上交点的数值来唯一标识行，列和正/反对角线。相应的规则为：

求解通过灯坐标的行直线与 x 轴的交点，将交点的 x 坐标作为通过灯坐标的行的数值。
求解通过灯坐标的列直线与 y 轴的交点，将交点的 y 坐标作为通过灯坐标的列的数值。
求解通过灯坐标的正对角线与 x 轴的交点，将交点的 x 坐标作为通过灯坐标的正对角线的数值。
求解通过灯坐标的反对角线与 y 轴的交点，将交点的 y 坐标作为通过灯坐标的反对角线的数值。

假设一盏灯的坐标为 (x_i,~y_i)，那么它所在的行的数值为 x_i，列的数值为 y_i，正对角线的数值为 x_i-y_i，反对角线的数值为 x_i+y_i。确定某一直线的唯一数值标识后，我们就可以通过哈希表来记录某一直线所拥有的灯的数目。

遍历 lamps，将当前遍历到的灯所在的行，列和正/反对角线拥有灯的数目分别加一。

在处理 lamps 时，需要进行去重，因为我们将重复的灯看作同一盏灯。

遍历 queries，判断当前查询点所在的行，列和正/反对角线是否有灯，如果有，则置 1，即该点在查询时是被照亮的。然后进行关闭操作，查找查询点所在的八近邻点及它本身是否有灯，如果有，将该点所在的行，列和正/反对角线的灯数目分别减一，并且将灯从网格中去掉。

代码

[sol1-Python3]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution:
    def gridIllumination(self, n: int, lamps: List[List[int]], queries: List[List[int]]) -> List[int]:
        points = set()
        row, col, diagonal, antiDiagonal = Counter(), Counter(), Counter(), Counter()
        for r, c in lamps:
            if (r, c) in points:
                continue
            points.add((r, c))
            row[r] += 1
            col[c] += 1
            diagonal[r - c] += 1
            antiDiagonal[r + c] += 1

        ans = [0] * len(queries)
        for i, (r, c) in enumerate(queries):
            if row[r] or col[c] or diagonal[r - c] or antiDiagonal[r + c]:
                ans[i] = 1
            for x in range(r - 1, r + 2):
                for y in range(c - 1, c + 2):
                    if x < 0 or y < 0 or x >= n or y >= n or (x, y) not in points:
                        continue
                    points.remove((x, y))
                    row[x] -= 1
                    col[y] -= 1
                    diagonal[x - y] -= 1
                    antiDiagonal[x + y] -= 1
        return ans
[sol1-C++]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
class Solution {
public:
    vector<int> gridIllumination(int n, vector<vector<int>> &lamps, vector<vector<int>> &queries) {
        unordered_map<int, int> row, col, diagonal, antiDiagonal;
        auto hash_p = [](const pair<int, int> &p) -> size_t {
            static hash<long long> hash_ll;
            return hash_ll(p.first + (static_cast<long long>(p.second) << 32));
        };
        unordered_set<pair<int, int>, decltype(hash_p)> points(0, hash_p);
        for (auto &lamp : lamps) {
            if (points.count({lamp[0], lamp[1]}) > 0) {
                continue;
            }
            points.insert({lamp[0], lamp[1]});
            row[lamp[0]]++;
            col[lamp[1]]++;
            diagonal[lamp[0] - lamp[1]]++;
            antiDiagonal[lamp[0] + lamp[1]]++;
        }
        vector<int> ret(queries.size());
        for (int i = 0; i < queries.size(); i++) {
            int r = queries[i][0], c = queries[i][1];
            if (row.count(r) > 0 && row[r] > 0) {
                ret[i] = 1;
            } else if (col.count(c) > 0 && col[c] > 0) {
                ret[i] = 1;
            } else if (diagonal.count(r - c) > 0 && diagonal[r - c] > 0) {
                ret[i] = 1;
            } else if (antiDiagonal.count(r + c) > 0 && antiDiagonal[r + c] > 0) {
                ret[i] = 1;
            }
            for (int x = r - 1; x <= r + 1; x++) {
                for (int y = c - 1; y <= c + 1; y++) {
                    if (x < 0 || y < 0 || x >= n || y >= n) {
                        continue;
                    }
                    auto p = points.find({x, y});
                    if (p != points.end()) {
                        points.erase(p);
                        row[x]--;
                        col[y]--;
                        diagonal[x - y]--;
                        antiDiagonal[x + y]--;
                    }
                }
            }
        }
        return ret;
    }
};
[sol1-Java]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Solution {
    public int[] gridIllumination(int n, int[][] lamps, int[][] queries) {
        Map<Integer, Integer> row = new HashMap<Integer, Integer>();
        Map<Integer, Integer> col = new HashMap<Integer, Integer>();
        Map<Integer, Integer> diagonal = new HashMap<Integer, Integer>();
        Map<Integer, Integer> antiDiagonal = new HashMap<Integer, Integer>();
        Set<Long> points = new HashSet<Long>();
        for (int[] lamp : lamps) {
            if (!points.add(hash(lamp[0], lamp[1]))) {
                continue;
            }
            row.put(lamp[0], row.getOrDefault(lamp[0], 0) + 1);
            col.put(lamp[1], col.getOrDefault(lamp[1], 0) + 1);
            diagonal.put(lamp[0] - lamp[1], diagonal.getOrDefault(lamp[0] - lamp[1], 0) + 1);
            antiDiagonal.put(lamp[0] + lamp[1], antiDiagonal.getOrDefault(lamp[0] + lamp[1], 0) + 1);
        }
        int[] ret = new int[queries.length];
        for (int i = 0; i < queries.length; i++) {
            int r = queries[i][0], c = queries[i][1];
            if (row.getOrDefault(r, 0) > 0) {
                ret[i] = 1;
            } else if (col.getOrDefault(c, 0) > 0) {
                ret[i] = 1;
            } else if (diagonal.getOrDefault(r - c, 0) > 0) {
                ret[i] = 1;
            } else if (antiDiagonal.getOrDefault(r + c, 0) > 0) {
                ret[i] = 1;
            }
            for (int x = r - 1; x <= r + 1; x++) {
                for (int y = c - 1; y <= c + 1; y++) {
                    if (x < 0 || y < 0 || x >= n || y >= n) {
                        continue;
                    }
                    if (points.remove(hash(x, y))) {
                        row.put(x, row.get(x) - 1);
                        if (row.get(x) == 0) {
                            row.remove(x);
                        }
                        col.put(y, col.get(y) - 1);
                        if (col.get(y) == 0) {
                            col.remove(y);
                        }
                        diagonal.put(x - y, diagonal.get(x - y) - 1);
                        if (diagonal.get(x - y) == 0) {
                            diagonal.remove(x - y);
                        }
                        antiDiagonal.put(x + y, antiDiagonal.get(x + y) - 1);
                        if (antiDiagonal.get(x + y) == 0) {
                            antiDiagonal.remove(x + y);
                        }
                    }
                }
            }
        }
        return ret;
    }

    public long hash(int x, int y) {
        return (long) x + ((long) y << 32);
    }
}
[sol1-C#]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
public class Solution {
    public int[] GridIllumination(int n, int[][] lamps, int[][] queries) {
        Dictionary<int, int> row = new Dictionary<int, int>();
        Dictionary<int, int> col = new Dictionary<int, int>();
        Dictionary<int, int> diagonal = new Dictionary<int, int>();
        Dictionary<int, int> antiDiagonal = new Dictionary<int, int>();
        ISet<long> points = new HashSet<long>();
        foreach (int[] lamp in lamps) {
            if (!points.Add(Hash(lamp[0], lamp[1]))) {
                continue;
            }
            if (!row.ContainsKey(lamp[0])) {
                row.Add(lamp[0], 0);
            }
            row[lamp[0]]++;
            if (!col.ContainsKey(lamp[1])) {
                col.Add(lamp[1], 0);
            }
            col[lamp[1]]++;
            if (!diagonal.ContainsKey(lamp[0] - lamp[1])) {
                diagonal.Add(lamp[0] - lamp[1], 0);
            }
            diagonal[lamp[0] - lamp[1]]++;
            if (!antiDiagonal.ContainsKey(lamp[0] + lamp[1])) {
                antiDiagonal.Add(lamp[0] + lamp[1], 0);
            }
            antiDiagonal[lamp[0] + lamp[1]]++;
        }
        int[] ret = new int[queries.Length];
        for (int i = 0; i < queries.Length; i++) {
            int r = queries[i][0], c = queries[i][1];
            if (row.ContainsKey(r) && row[r] > 0) {
                ret[i] = 1;
            } else if (col.ContainsKey(c) && col[c] > 0) {
                ret[i] = 1;
            } else if (diagonal.ContainsKey(r - c) && diagonal[r - c] > 0) {
                ret[i] = 1;
            } else if (antiDiagonal.ContainsKey(r + c) && antiDiagonal[r + c] > 0) {
                ret[i] = 1;
            }
            for (int x = r - 1; x <= r + 1; x++) {
                for (int y = c - 1; y <= c + 1; y++) {
                    if (x < 0 || y < 0 || x >= n || y >= n) {
                        continue;
                    }
                    if (points.Remove(Hash(x, y))) {
                        row[x]--;
                        if (row[x] == 0) {
                            row.Remove(x);
                        }
                        col[y]--;
                        if (col[y] == 0) {
                            col.Remove(y);
                        }
                        diagonal[x - y]--;
                        if (diagonal[x - y] == 0) {
                            diagonal.Remove(x - y);
                        }
                        antiDiagonal[x + y]--;
                        if (antiDiagonal[x + y] == 0) {
                            antiDiagonal.Remove(x + y);
                        }
                    }
                }
            }
        }
        return ret;
    }

    public long Hash(int x, int y) {
        return (long) x + ((long) y << 32);
    }
}
[sol1-C]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
typedef struct {
    long long key;
    int val;
    UT_hash_handle hh;
} HashEntry;

static inline long long hash(int x, int y) {
    return (long long) x + ((long long) y << 32);
}

void hashInsert(HashEntry ** obj, long long key) {
    HashEntry * pEntry = NULL;
    HASH_FIND(hh, *obj, &key, sizeof(long long), pEntry);
    if (NULL == pEntry) {
        pEntry = (HashEntry *)malloc(sizeof(HashEntry));
        pEntry->key = key;
        pEntry->val = 1;
        HASH_ADD(hh, *obj, key, sizeof(long long), pEntry);
    } else {
        pEntry->val++;
    }
}

void hashErase(HashEntry ** obj, long long key) {
    HashEntry * pEntry = NULL;
    HASH_FIND(hh, *obj, &key, sizeof(long long), pEntry);
    if (NULL != pEntry) {
        pEntry->val -= 1;
        if (pEntry->val == 0) {
            HASH_DEL(*obj, pEntry);
            free(pEntry);
        }
    }
}

void hashDelete(HashEntry ** obj, long long key) {
    HashEntry * pEntry = NULL;
    HASH_FIND(hh, *obj, &key, sizeof(long long), pEntry);
    if (NULL != pEntry) {
        HASH_DEL(*obj, pEntry);
        free(pEntry);
    }
}

bool hashFind(HashEntry ** obj, long long key) {
    HashEntry * pEntry = NULL;
    HASH_FIND(hh, *obj, &key, sizeof(long long), pEntry);
    if (NULL == pEntry) {
        return false;
    } else {
        return true;
    }
}

void hashFreeAll(HashEntry ** obj) {
    HashEntry *curr, *next;
    HASH_ITER(hh, *obj, curr, next) {
        HASH_DEL(*obj, curr);  
        free(curr);
    }
}

int* gridIllumination(int n, int** lamps, int lampsSize, int* lampsColSize, int** queries, int queriesSize, int* queriesColSize, int* returnSize){
    HashEntry * row = NULL, * col = NULL;
    HashEntry * diagonal = NULL, * antiDiagonal = NULL;
    HashEntry * points = NULL;
    for (int i = 0; i < lampsSize; i++) {
        HashEntry * pEntry = NULL;
        long long p = hash(lamps[i][0], lamps[i][1]);
        HASH_FIND(hh, points, &p, sizeof(long long), pEntry);
        if (NULL != pEntry) {
            continue;
        }
        hashInsert(&points, p);
        hashInsert(&row, (long long)lamps[i][0]);
        hashInsert(&col, (long long)lamps[i][1]);
        hashInsert(&diagonal, (long long)(lamps[i][0] - lamps[i][1]));
        hashInsert(&antiDiagonal, (long long)(lamps[i][0] + lamps[i][1]));
    }

    int * ret = (int *)malloc(sizeof(int) * queriesSize);
    memset(ret, 0, sizeof(int) * queriesSize);
    for (int i = 0; i < queriesSize; i++) {
        int r = queries[i][0], c = queries[i][1];
        if (hashFind(&row, (long long)r)) {
            ret[i] = 1;
        } else if (hashFind(&col, (long long)c)) {
            ret[i] = 1;
        } else if (hashFind(&diagonal, (long long)(r - c))) {
            ret[i] = 1;
        } else if (hashFind(&antiDiagonal, (long long)(r + c))) {
            ret[i] = 1;
        }
        for (int x = r - 1; x <= r + 1; x++) {
            for (int y = c - 1; y <= c + 1; y++) {
                if (x < 0 || y < 0 || x >= n || y >= n) {
                    continue;
                }
                if (hashFind(&points, hash(x, y))) {
                    hashDelete(&points, hash(x, y));
                    hashErase(&row, (long long)x);
                    hashErase(&col, (long long)y);
                    hashErase(&diagonal, (long long)(x - y));
                    hashErase(&antiDiagonal, (long long)(x + y));
                }
            }
        }
    }
    hashFreeAll(&points);
    hashFreeAll(&row);
    hashFreeAll(&col);
    hashFreeAll(&diagonal);
    hashFreeAll(&antiDiagonal);
    *returnSize = queriesSize;
    return ret;
}
[sol1-Golang]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func gridIllumination(n int, lamps, queries [][]int) []int {
    type pair struct{ x, y int }
    points := map[pair]bool{}
    row := map[int]int{}
    col := map[int]int{}
    diagonal := map[int]int{}
    antiDiagonal := map[int]int{}
    for _, lamp := range lamps {
        r, c := lamp[0], lamp[1]
        p := pair{r, c}
        if points[p] {
            continue
        }
        points[p] = true
        row[r]++
        col[c]++
        diagonal[r-c]++
        antiDiagonal[r+c]++
    }

    ans := make([]int, len(queries))
    for i, query := range queries {
        r, c := query[0], query[1]
        if row[r] > 0 || col[c] > 0 || diagonal[r-c] > 0 || antiDiagonal[r+c] > 0 {
            ans[i] = 1
        }
        for x := r - 1; x <= r+1; x++ {
            for y := c - 1; y <= c+1; y++ {
                if x < 0 || y < 0 || x >= n || y >= n || !points[pair{x, y}] {
                    continue
                }
                delete(points, pair{x, y})
                row[x]--
                col[y]--
                diagonal[x-y]--
                antiDiagonal[x+y]--
            }
        }
    }
    return ans
}
[sol1-JavaScript]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
var gridIllumination = function(n, lamps, queries) {
    const row = new Map();
    const col = new Map();
    const diagonal = new Map();
    const antiDiagonal = new Map();
    const points = new Set();
    for (const lamp of lamps) {
        if (points.has(hash(lamp[0], lamp[1]))) {
            continue;
        }
        points.add(hash(lamp[0], lamp[1]));
        row.set(lamp[0], (row.get(lamp[0]) || 0) + 1);
        col.set(lamp[1], (col.get(lamp[1]) || 0) + 1);
        diagonal.set(lamp[0] - lamp[1], (diagonal.get(lamp[0] - lamp[1]) || 0) + 1);
        antiDiagonal.set(lamp[0] + lamp[1], (antiDiagonal.get(lamp[0] + lamp[1]) || 0) + 1);
    }
    const ret = new Array(queries.length).fill(0);
    for (const [i, [r, c]] of queries.entries()) {
        if (row.get(r) || col.get(c) || diagonal.get(r - c) || antiDiagonal.get(r + c)) {
            ret[i] = 1;
        }
        for (let x = r - 1; x < r + 2; x++) {
            for (let y = c - 1; y < c + 2; y++) {
                if (x < 0 || y < 0 || x >= n || y >= n || !points.has(hash(x, y))) {
                    continue;
                }
                points.delete(hash(x, y));
                row.set(x, row.get(x) - 1);
                col.set(y, col.get(y) - 1);
                diagonal.set(x - y, diagonal.get(x - y) - 1);
                antiDiagonal.set(x + y, antiDiagonal.get(x + y) - 1);
            }
        }
    }
    return ret;
}

const hash = (x, y) => {
    return x + ',' + y;
};

复杂度分析

  • 时间复杂度：O(l+q)，其中 l 和 q 分别是 lamps 和 queries 的长度。遍历两个数组的时间复杂度分别为 O(l) 和 O(q)。

  • 空间复杂度：O(l)。保存 5 个哈希表需要 O(l) 的空间，返回值不计入空间复杂度。

 Comments
On this page
1001-网格照明