给定一个整数数组,它表示BST(即 二叉搜索树 )的 先 序遍历 ,构造树并返回其根。
保证 对于给定的测试用例,总是有可能找到具有给定需求的二叉搜索树。
二叉搜索树 是一棵二叉树,其中每个节点, Node.left 的任何后代的值 严格小于 Node.val ,
Node.right 的任何后代的值 严格大于 Node.val。
二叉树的 前序遍历 首先显示节点的值,然后遍历Node.left,最后遍历Node.right。
示例 1:

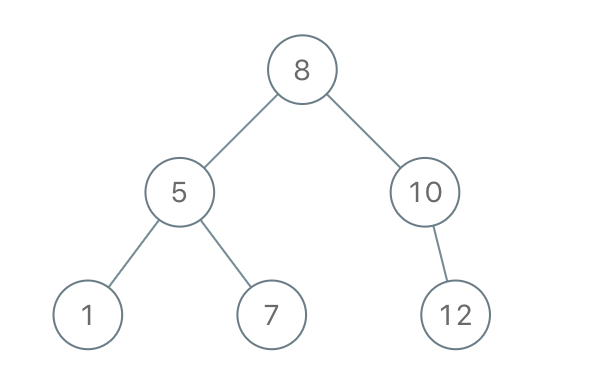
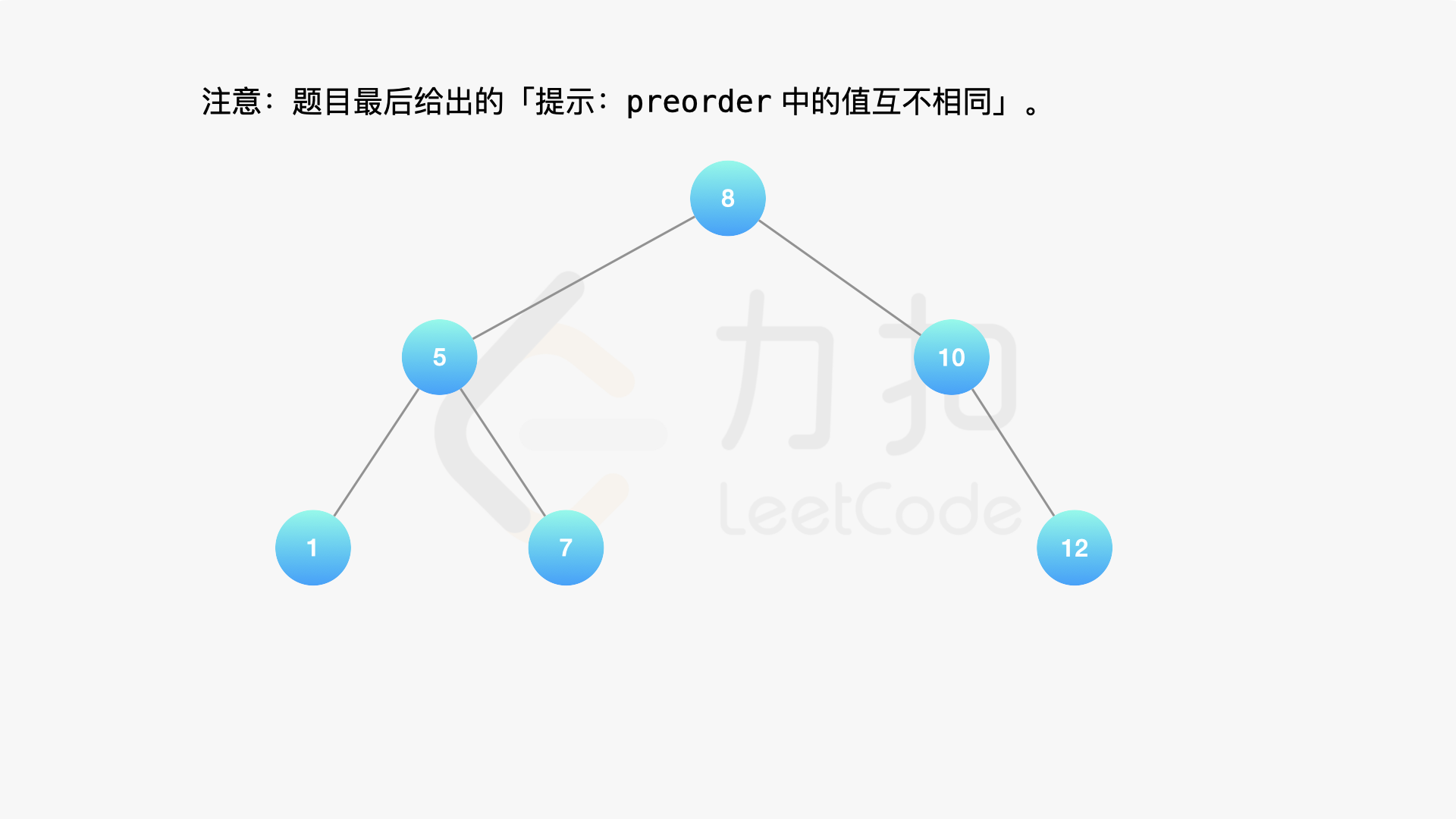
**输入:** preorder = [8,5,1,7,10,12]
**输出:** [8,5,10,1,7,null,12]
示例 2:
**输入:** preorder = [1,3]
**输出:** [1,null,3]
提示:
1 <= preorder.length <= 1001 <= preorder[i] <= 10^8preorder 中的值 互不相同
方法一:使用先序遍历和中序遍历构造二叉树
分析
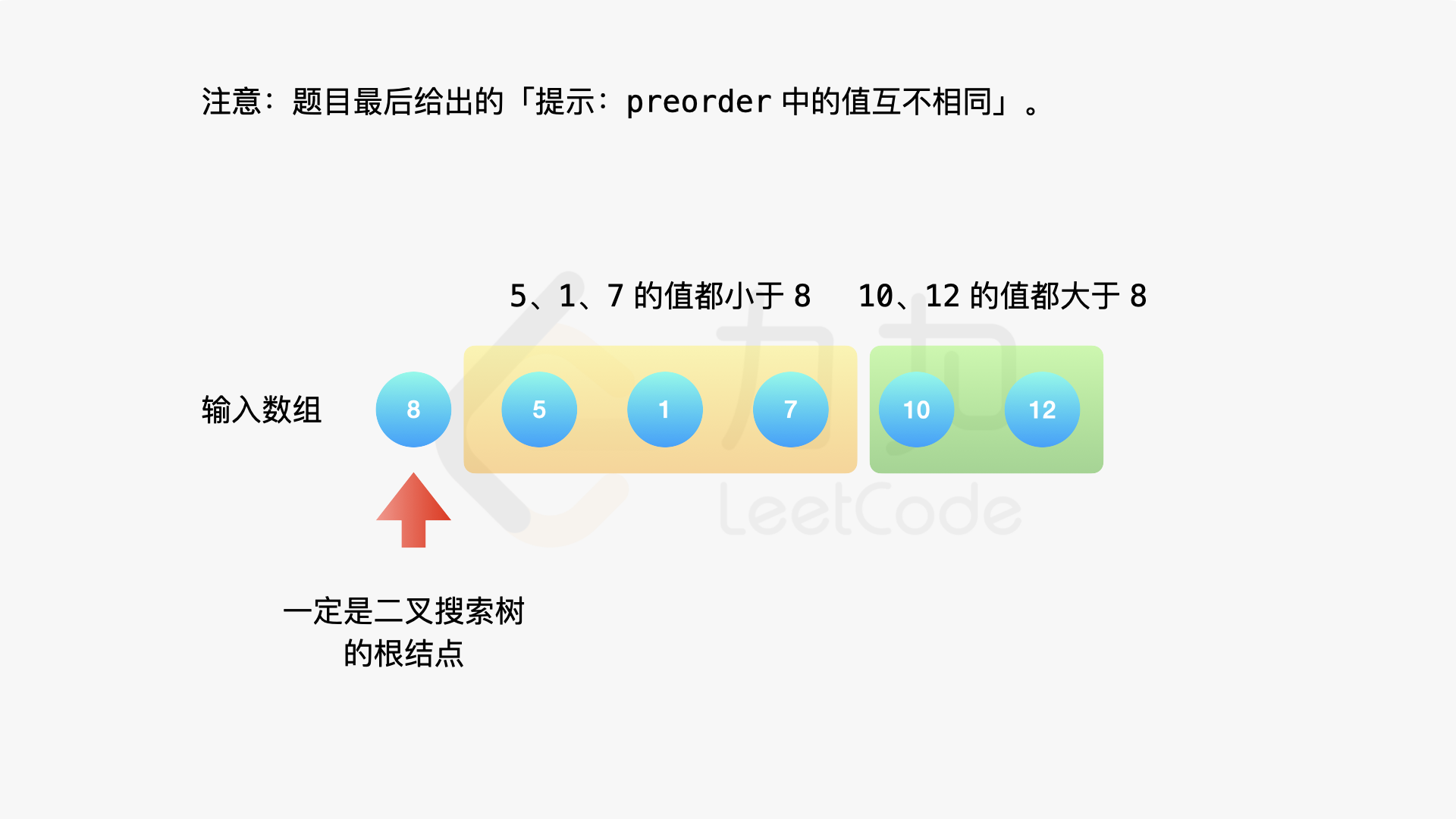
由于树是「二叉搜索树」,我们知道「二叉搜索树」的中序遍历的结果是有序序列。我们可以对「前序遍历」的结果 排序 得到「中序遍历」的结果。于是问题就转换成为 105. 从前序与中序遍历序列构造二叉树,该题也是一道非常经典的二叉树问题,读者可以参考 官方题解 。
代码
[]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| import java.util.Arrays;
import java.util.HashMap;
import java.util.Map;
public class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
int len = preorder.length;
Map<Integer, Integer> hashMap = new HashMap<>();
int[] inorder = new int[len];
System.arraycopy(preorder, 0, inorder, 0, len);
Arrays.sort(inorder);
int index = 0;
for (Integer value : inorder) {
hashMap.put(value, index);
index++;
}
return dfs(0, len - 1, 0, len - 1, preorder, hashMap);
}
public TreeNode dfs(int preLeft, int preRight, int inLeft, int inRight, int[] preorder, Map<Integer, Integer> hashMap) {
if (preLeft > preRight || inLeft > inRight) {
return null;
}
int pivot = preorder[preLeft];
TreeNode root = new TreeNode(pivot);
int pivotIndex = hashMap.get(pivot);
root.left = dfs(preLeft + 1, pivotIndex - inLeft + preLeft,
inLeft, pivotIndex - 1, preorder, hashMap);
root.right = dfs(pivotIndex - inLeft + preLeft + 1, preRight,
pivotIndex + 1, inRight, preorder, hashMap);
return root;
}
}
|
复杂度分析
- 时间复杂度:O(N \log N)。对先序遍历进行排序的时间复杂度为 O(N \log N),构造二叉搜索树的时间复杂度为 O(N),因此总的时间复杂度为 O(N \log N)。
- 空间复杂度:O(N),中序遍历使用的数组的空间为 O(N)。
方法二:二分查找左右子树的分界线递归构建左右子树
当我们「先序遍历序列」排序得到「中序遍历序列」时,我们花费了 O(N \log N) 的时间复杂度。但事实上并没有得到任何额外的信息。可以直接跳过生成中序遍历的步骤,根据先序遍历直接构造出二叉树。
根据「前序遍历」的定义:前序遍历的第 1 个结点一定是二叉树的根结点。
再根据「二叉搜索树」的定义:根据前序遍历的第 1 个结点的值可以把「前序遍历」序列除了第 1 个结点以外后面的部分,分为两个区间:
- 第 1 个子区间里所有的元素都严格小于根结点,我们可以递归构建成根结点的左子树;
- 第 2 个子区间里所有的元素都严格大于根结点,我们可以递归构建成根结点的右子树。
找到这两个子区间的分界线,可以使用二分查找。下面我们通过具体例子向大家展示这种方法。
< ,
, ,
, ,
, ,
, >
>
代码
[]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| public class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
int len = preorder.length;
if (len == 0) {
return null;
}
return dfs(preorder, 0, len - 1);
}
private TreeNode dfs(int[] preorder, int left, int right) {
if (left > right) {
return null;
}
TreeNode root = new TreeNode(preorder[left]);
if (left == right) {
return root;
}
int l = left;
int r = right;
while (l < r) {
int mid = l + (r - l + 1) / 2;
if (preorder[mid] < preorder[left]) {
l = mid;
} else {
r = mid - 1;
}
}
TreeNode leftTree = dfs(preorder, left + 1, l);
TreeNode rightTree = dfs(preorder, l + 1, right);
root.left = leftTree;
root.right = rightTree;
return root;
}
}
|
复杂度分析:
- 时间复杂度:O(N \log N),在找左右子树分界线的时候时间复杂度为 O(\log N);
- 空间复杂度:O(N)。
方法三:根据数值上下界递归构建左右子树
分析
由于题目中的二叉树是二叉搜索树,因此 根据先序遍历构造出的二叉树才是唯一的。
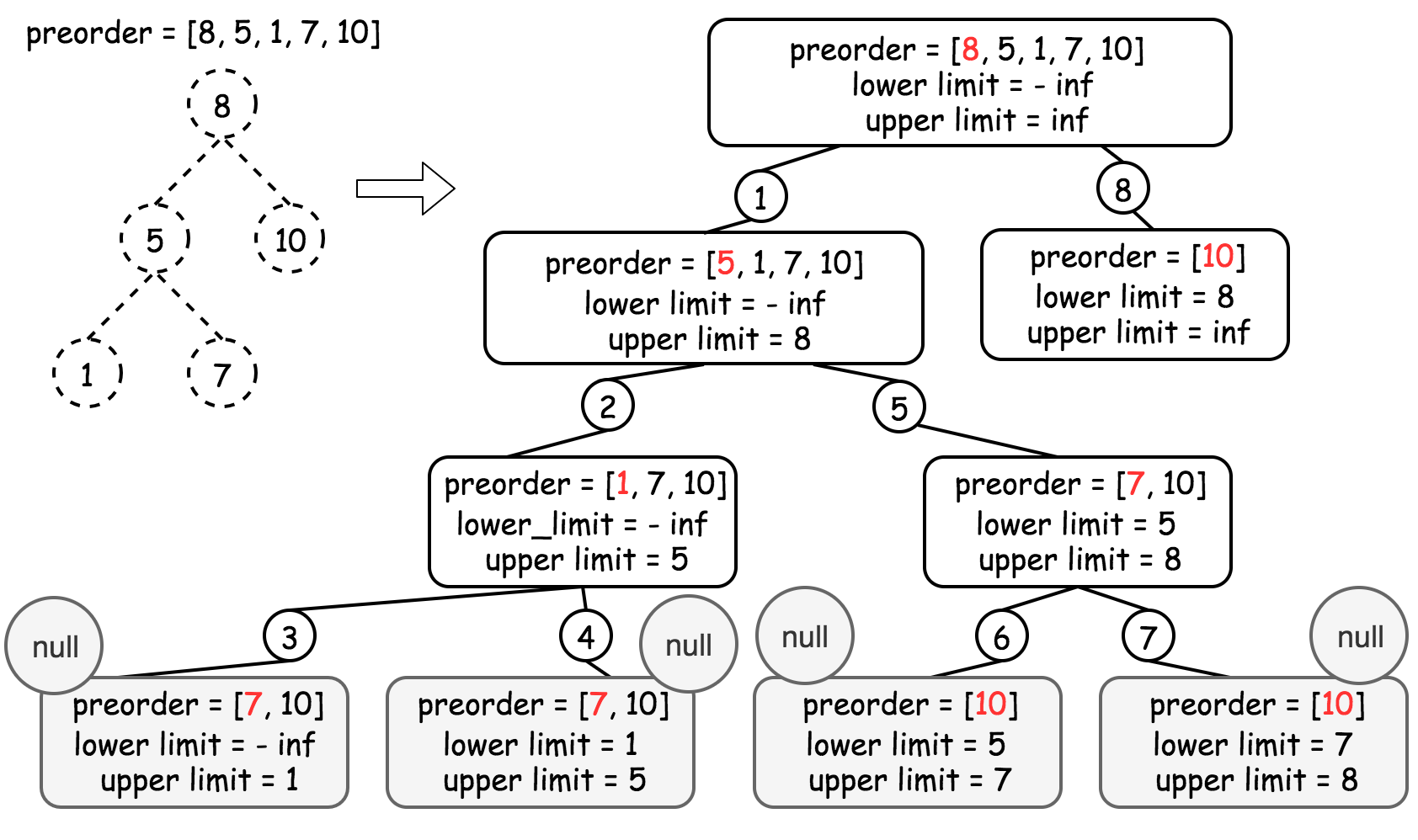
我们使用递归的方法,在扫描先序遍历的同时构造出二叉树。我们在递归时维护一个 (lower, upper) 二元组,表示当前位置可以插入的节点的值的上下界。如果此时先序遍历位置的值处于上下界中,就将这个值作为新的节点插入到当前位置,并递归地处理当前位置的左右孩子的两个位置。否则回溯到当前位置的父节点。
算法
- 将
lower 和 upper 的初始值分别设置为负无穷和正无穷,因为根节点的值可以为任意值。
- 从先序遍历的第一个元素
idx = 0 开始构造二叉树,构造使用的函数名为 helper(lower, upper):
- 如果
idx = n,即先序遍历中的所有元素已经被添加到二叉树中,那么此时构造已经完成;
- 如果当前
idx 对应的先序遍历中的元素 val = preorder[idx] 的值不在 [lower, upper] 范围内,则进行回溯;
- 如果
idx 对应的先序遍历中的元素 val = preorder[idx] 的值在 [lower, upper] 范围内,则新建一个节点 root,并对其左孩子递归处理 helper(lower, val),对其右孩子递归处理 helper(val, upper)。
下图展示了这个过程。
 {:width=600}
{:width=600}
{:align=center}
代码
[]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| public class Solution {
private int index = 0;
private int[] preorder;
private int len;
public TreeNode bstFromPreorder(int[] preorder) {
this.preorder = preorder;
this.len = preorder.length;
return dfs(Integer.MIN_VALUE, Integer.MAX_VALUE);
}
private TreeNode dfs(int lowerBound, int upperBound) {
if (index == len) {
return null;
}
int cur = preorder[index];
if (cur < lowerBound || cur > upperBound) {
return null;
}
index++;
TreeNode root = new TreeNode(cur);
root.left = dfs(lowerBound, cur);
root.right = dfs(cur, upperBound);
return root;
}
}
|
复杂度分析
- 时间复杂度:O(N),这里 N 是输入数组的长度。
- 空间复杂度:O(N)。
方法四:迭代
方法三中的递归可以借助「栈」迭代实现「递归」的功能。
算法
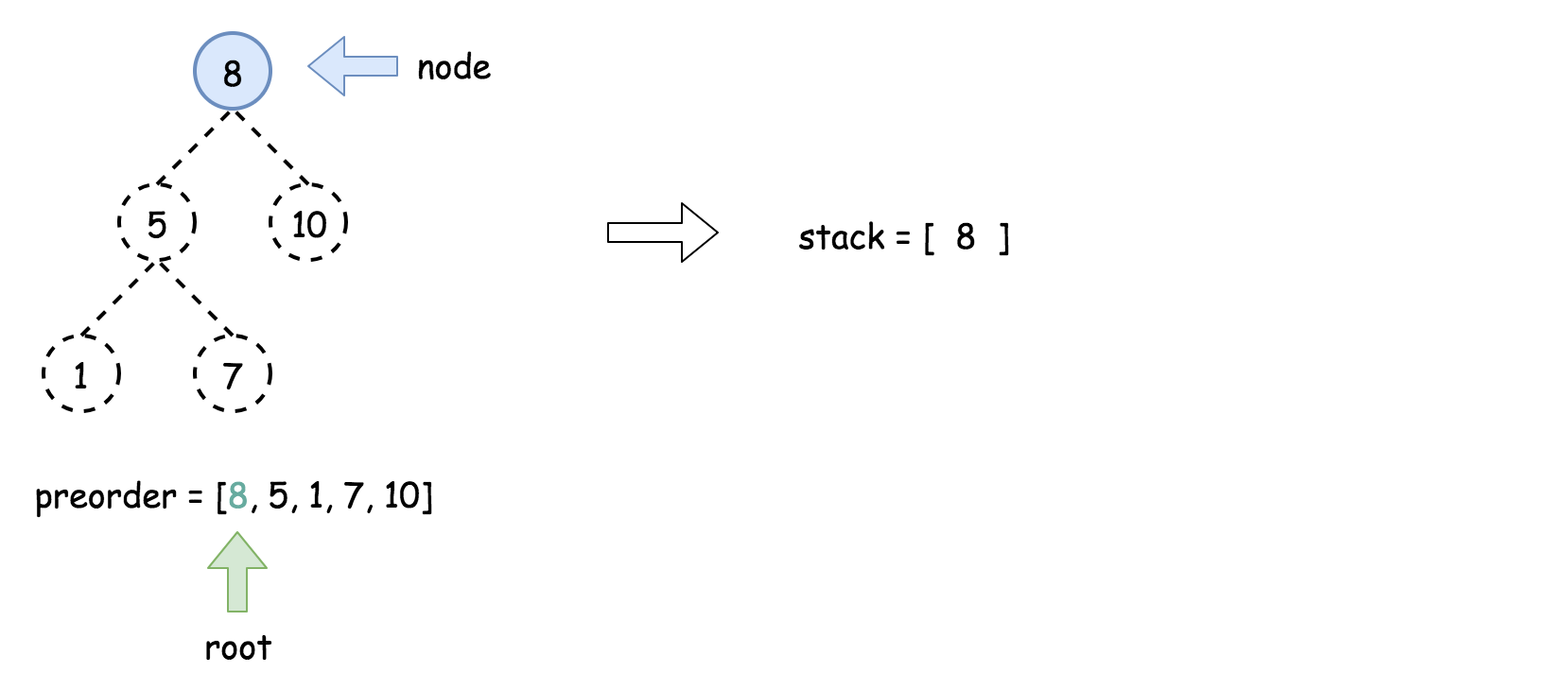
- 将先序遍历中的第一个元素作为二叉树的根节点,即
root = new TreeNode(preorder[0]),并将其放入栈中。
- 使用
for 循环迭代先序遍历中剩下的所有元素:
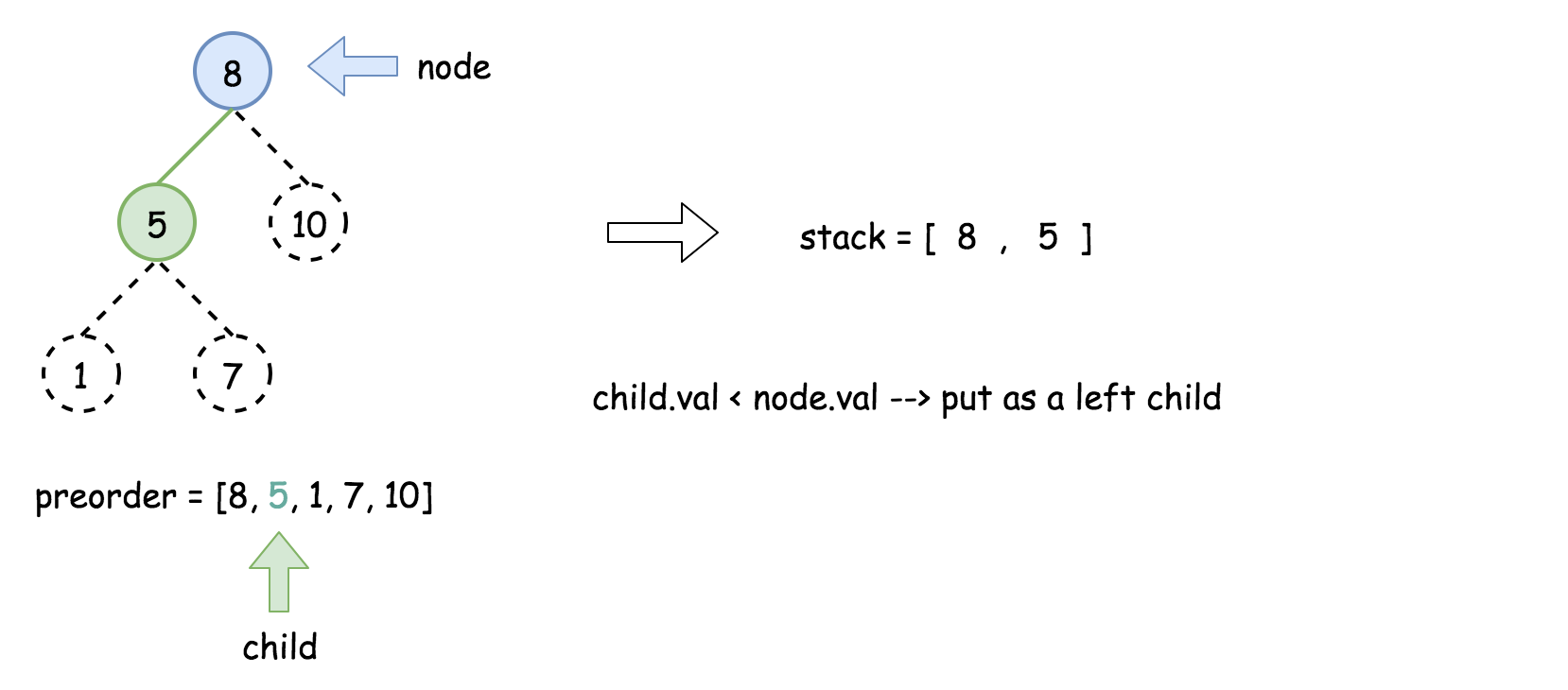
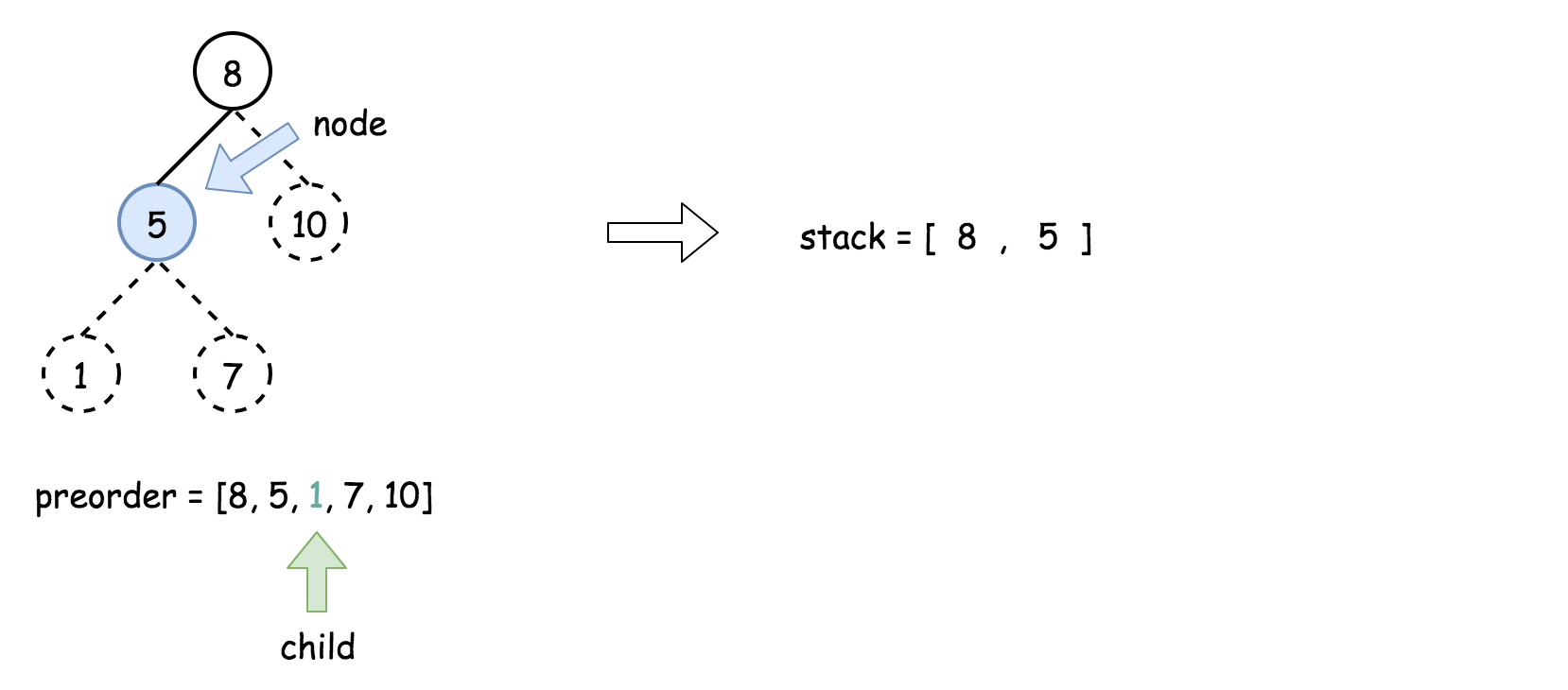
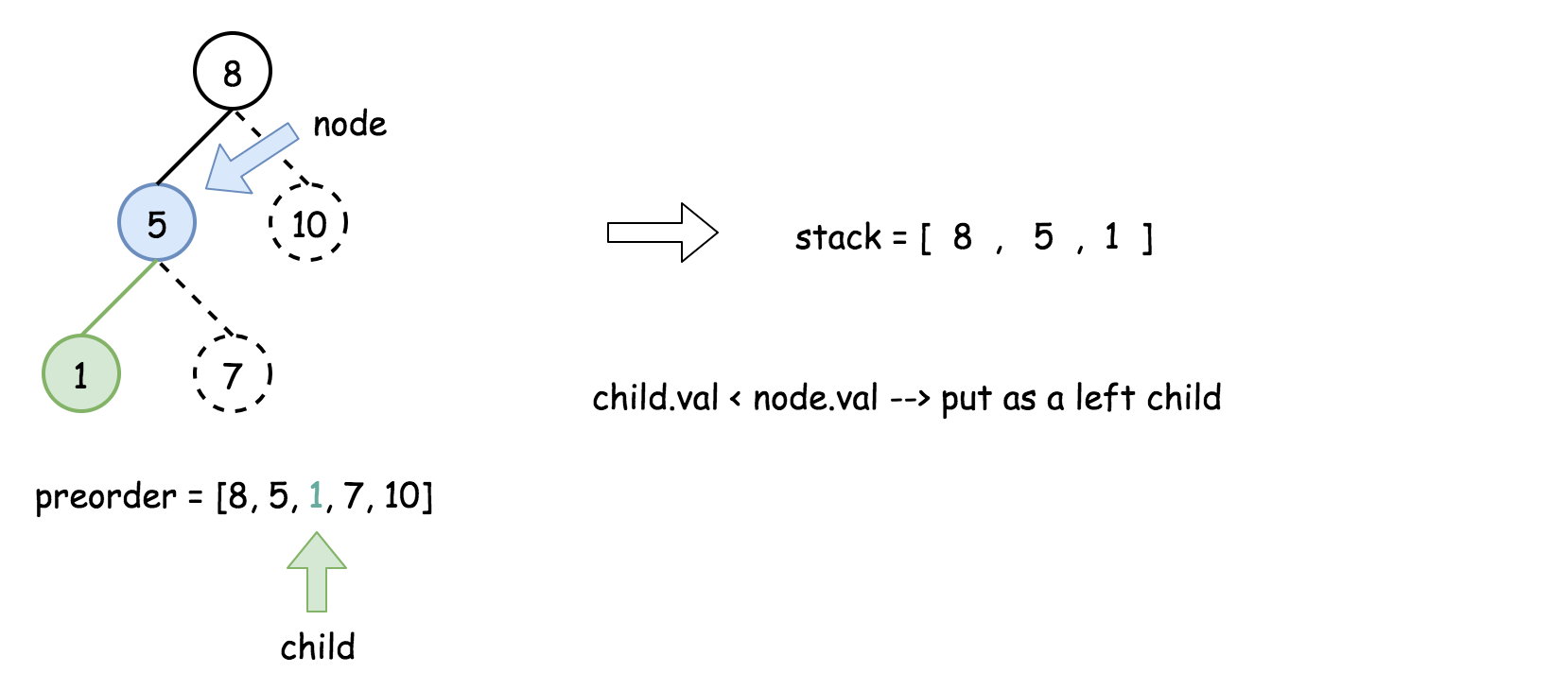
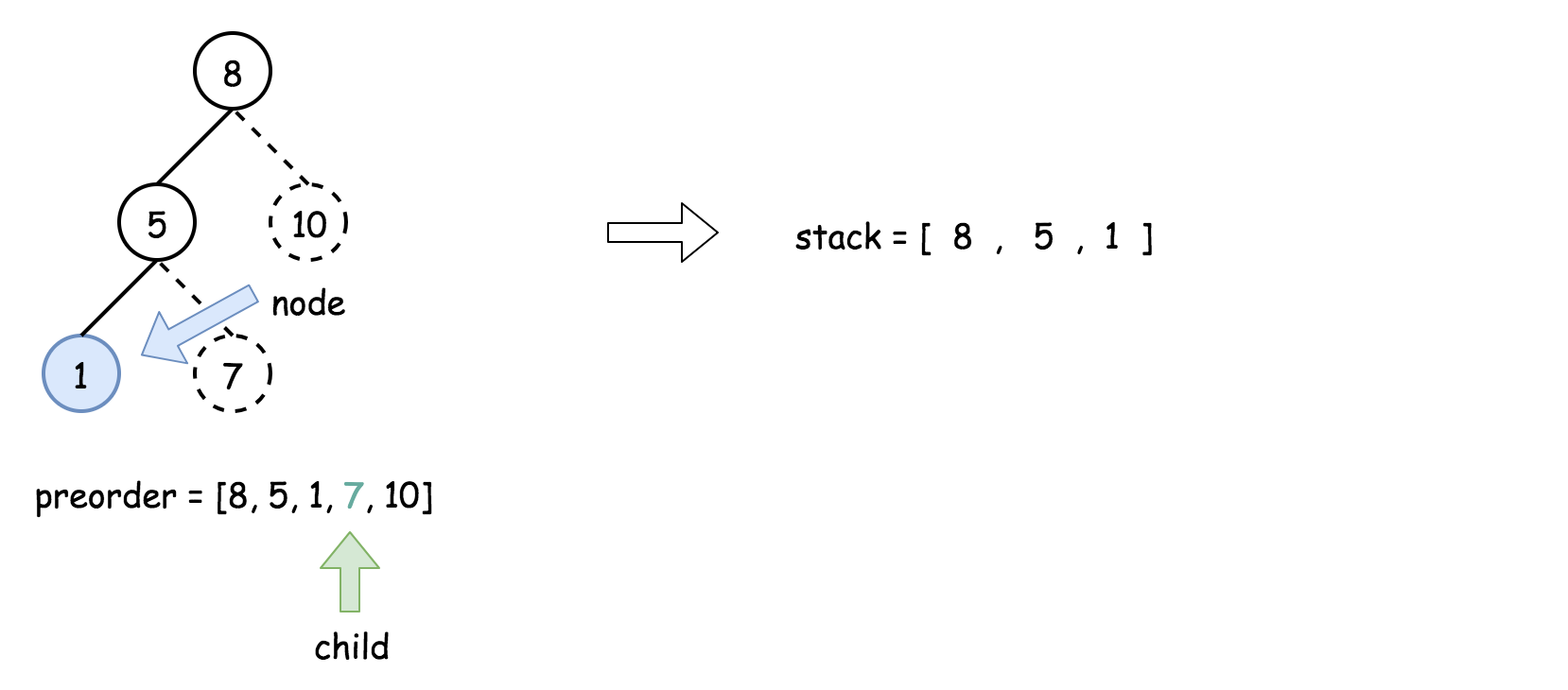
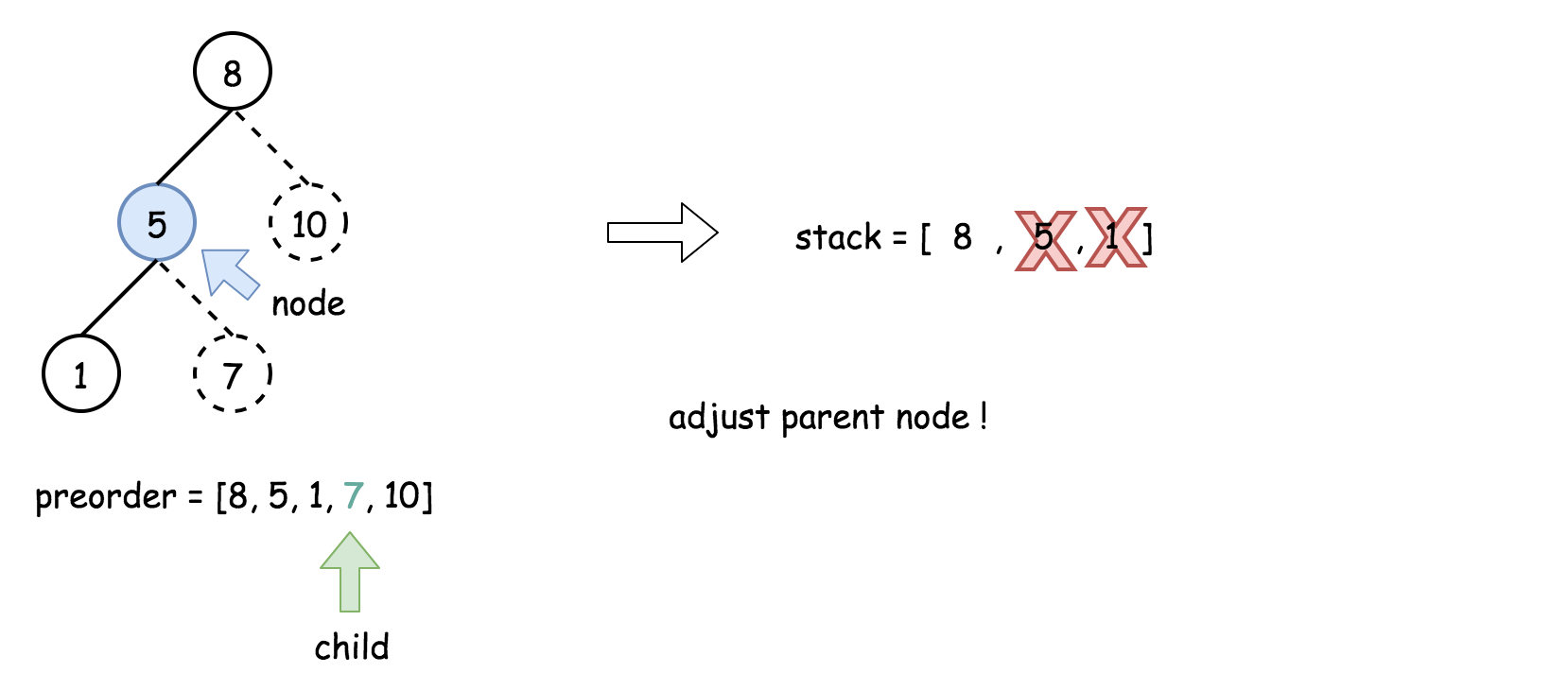
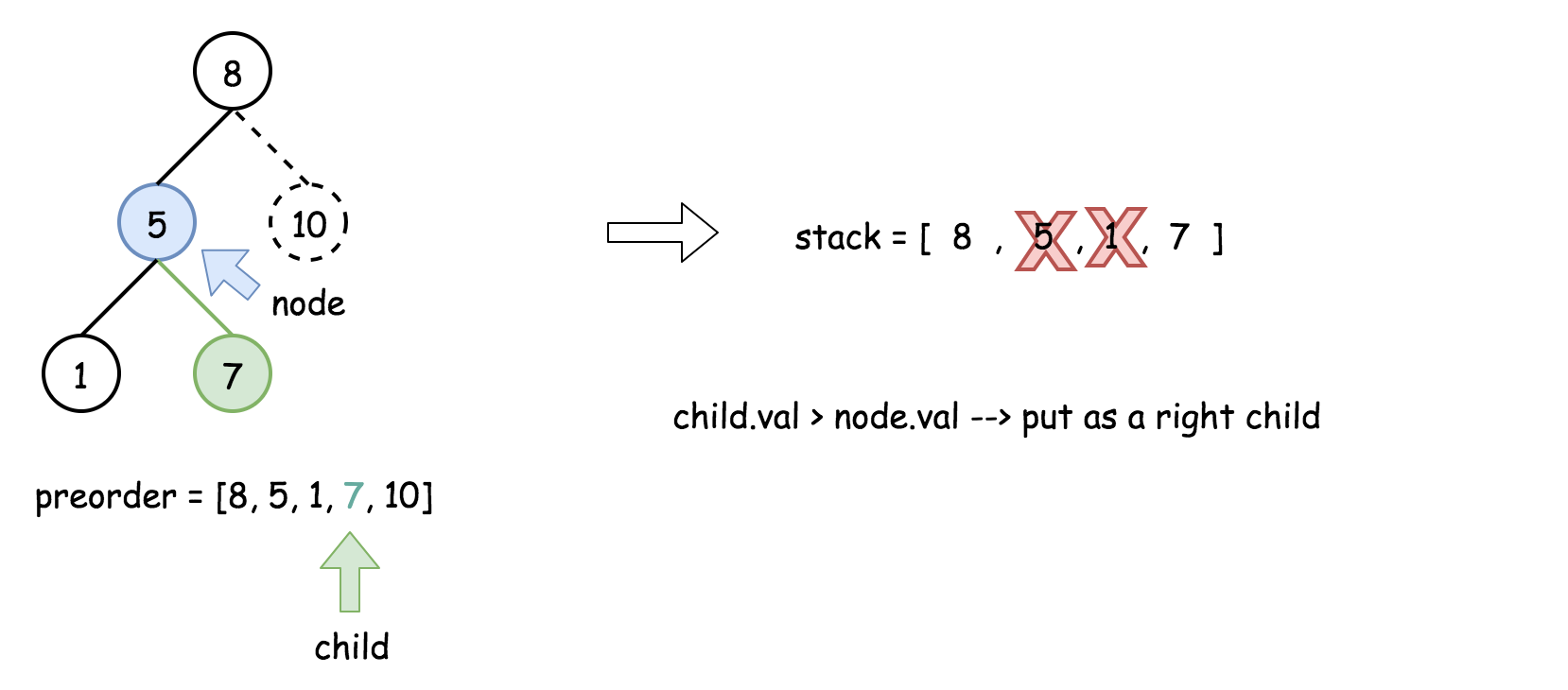
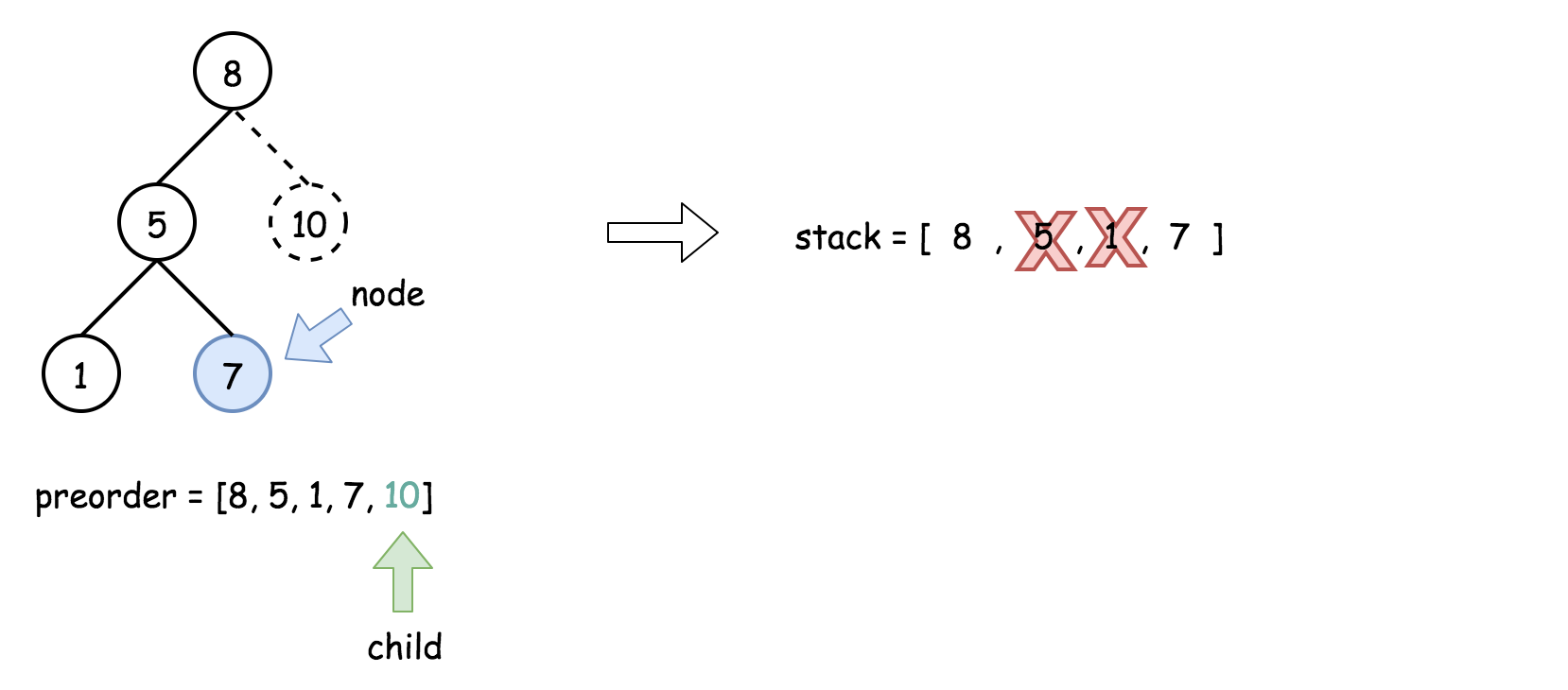
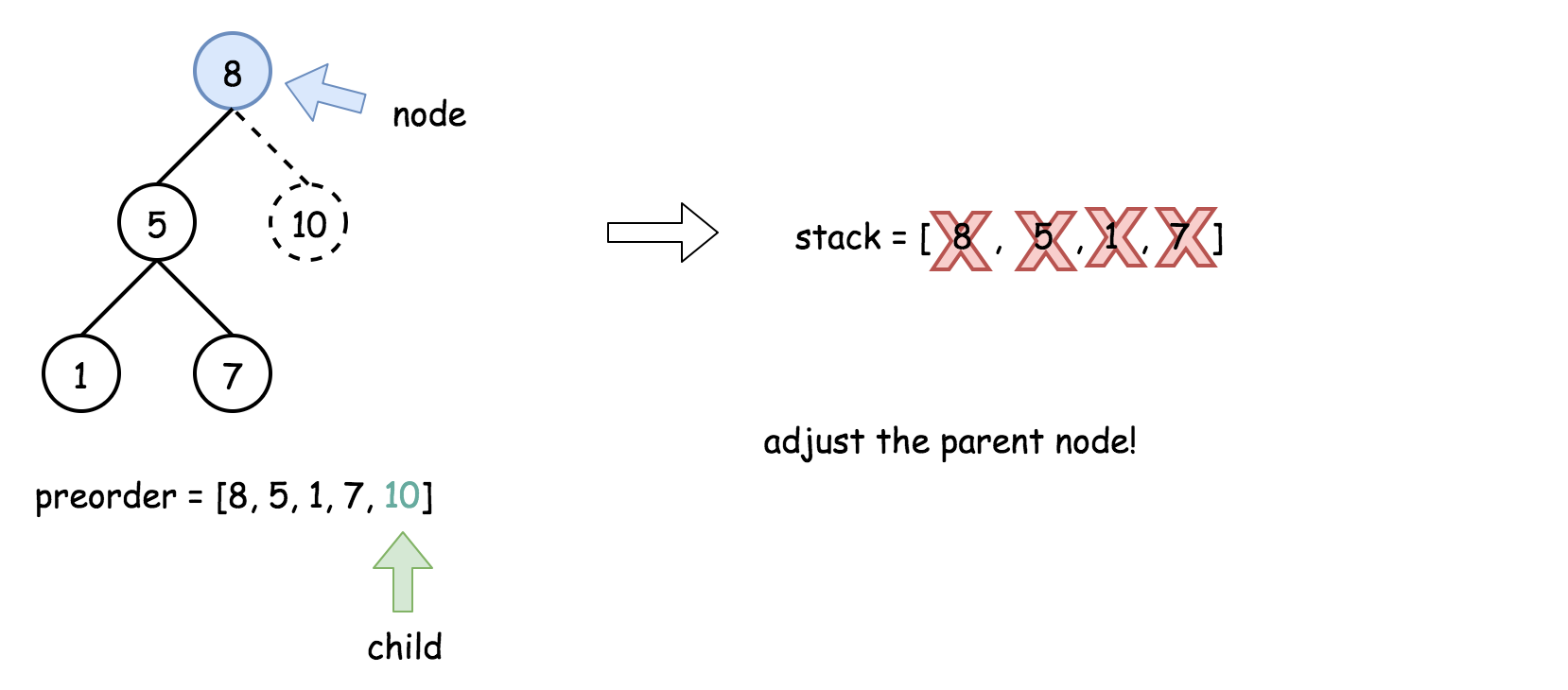
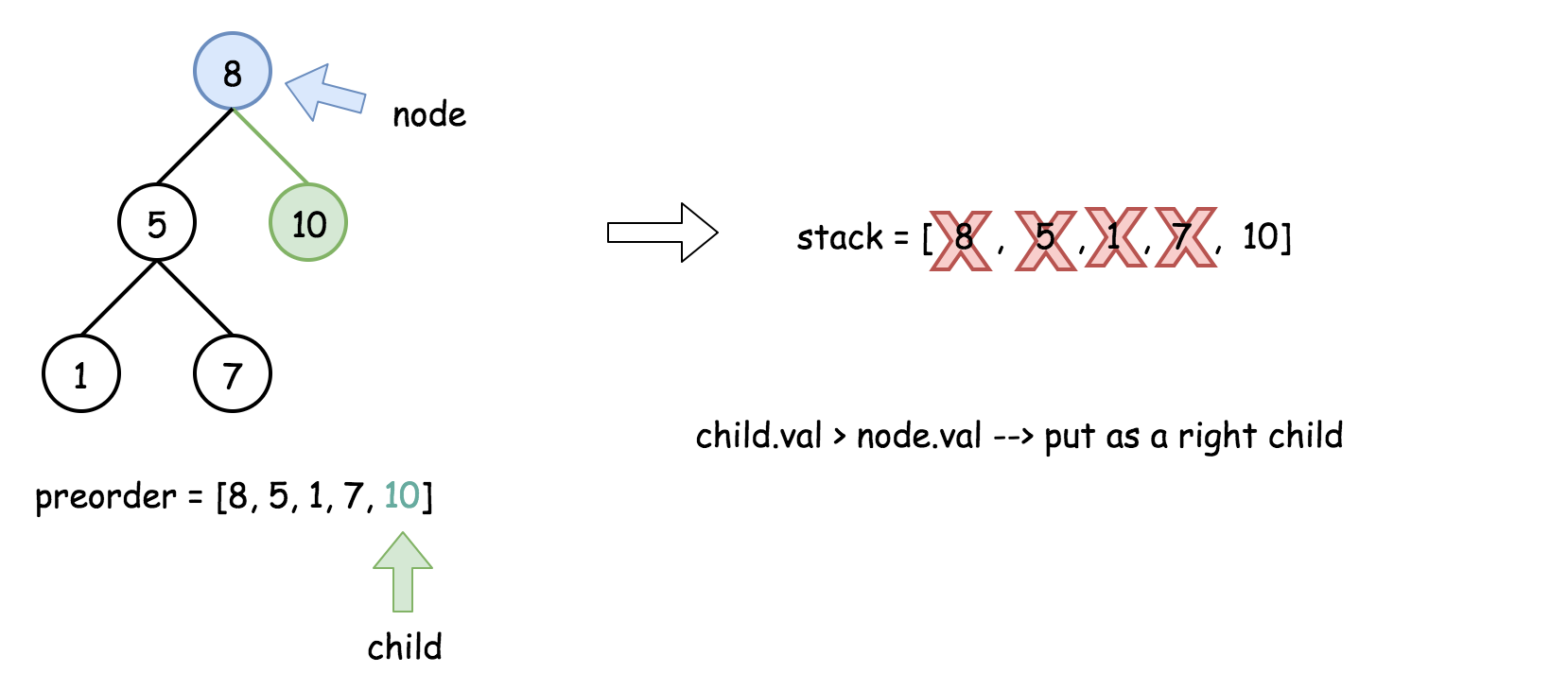
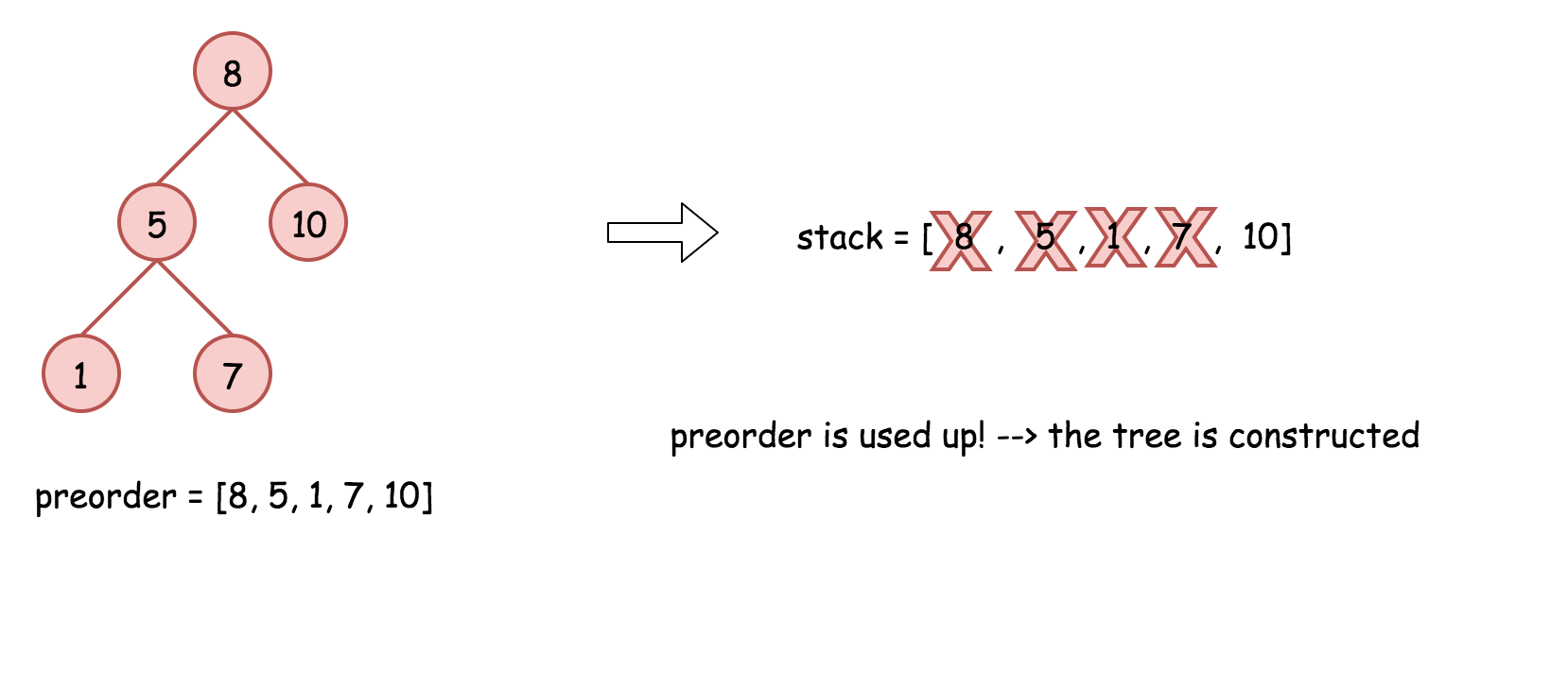
- 将栈顶的元素作为父节点,当前先序遍历中的元素作为子节点。如果栈顶的元素值小于子节点的元素值,则将栈顶的元素弹出并作为新的父节点,直到栈空或栈顶的元素值大于子节点的元素值。注意,这里作为父节点的是最后一个被弹出栈的元素,而不是此时栈顶的元素;
- 如果父节点的元素值小于子节点的元素值,则子节点为右孩子,否则为左孩子;
- 将子节点放入栈中。
下面的动画展示了这个过程。
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
代码
[]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| import java.util.ArrayDeque;
import java.util.Deque;
public class Solution {
public TreeNode bstFromPreorder(int[] preorder) {
int len = preorder.length;
if (len == 0) {
return null;
}
TreeNode root = new TreeNode(preorder[0]);
Deque<TreeNode> stack = new ArrayDeque<>();
stack.push(root);
for (int i = 1; i < len; i++) {
TreeNode node = stack.peekLast();
TreeNode currentNode = new TreeNode(preorder[i]);
while (!stack.isEmpty() && stack.peekLast().val < currentNode.val) {
node = stack.removeLast();
}
if (node.val < currentNode.val) {
node.right = currentNode;
} else {
node.left = currentNode;
}
stack.addLast(currentNode);
}
return root;
}
}
|
复杂度分析
- 时间复杂度:O(N),仅扫描前序遍历一次。
- 空间复杂度:O(N),用来存储栈和二叉树。
 ,
, ,
, ,
, ,
, >
> {:width=600}
{:width=600}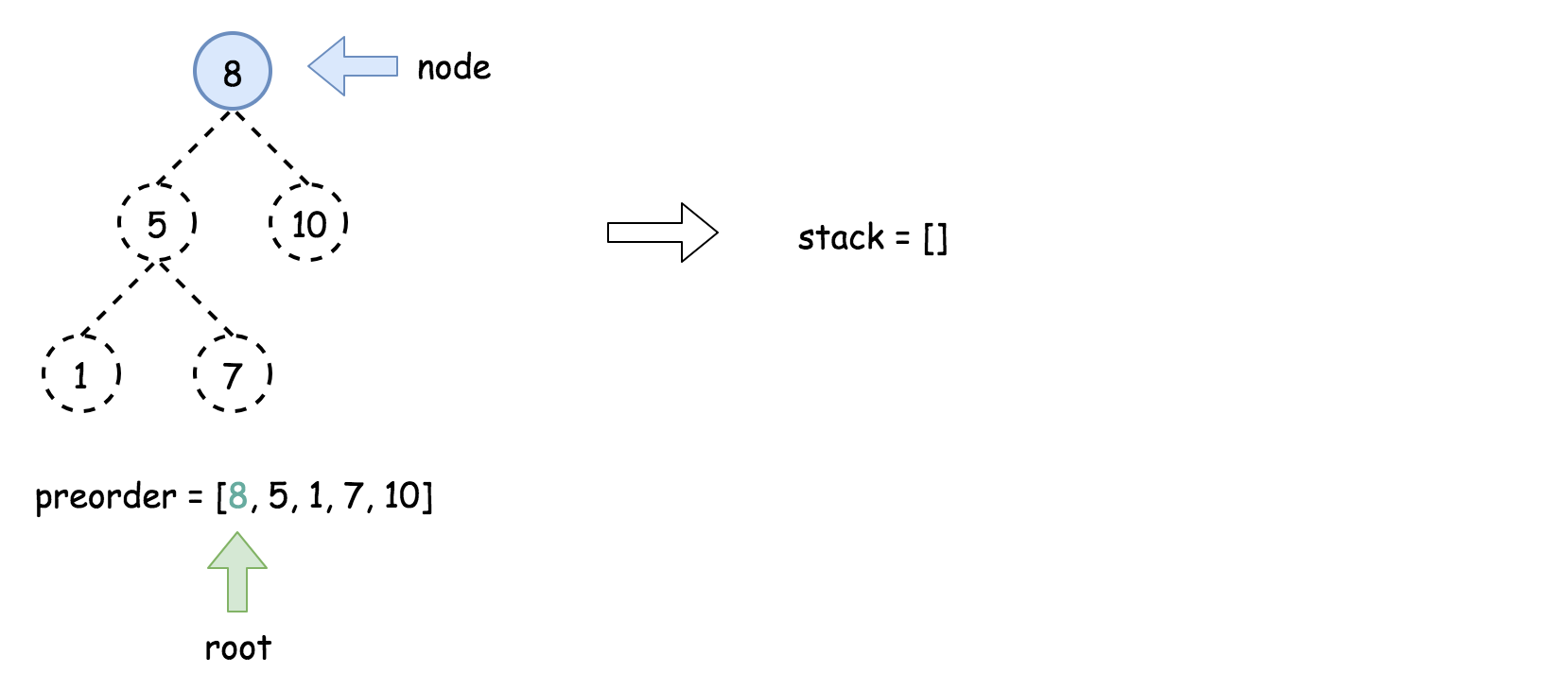 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>